河北省唐山市乐亭县2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-09-01 类型:期末考试
一、单选题
-
1.
如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
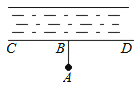 A、两点之间线段最短 B、点到直线的距离 C、两点确定一条直线 D、垂线段最短2. 如果 ,那么下列结论中一定成立的是( )A、 B、 C、 D、3. 下列运算正确的是( )A、(a2)3=a5 B、a8÷a4=a2 C、(a+b)2=a2+b2 D、(a﹣b)(a+b)=a2﹣b24. 把 写成 ( , 为整数)的形式,则 为( )A、 B、 C、 D、5. 方程2x+y=5与下列方程构成的方程组的解为 的是( )A、x﹣y=4 B、x+y=4 C、3x﹣y=8 D、x+2y=﹣16. 下列各式能用公式法因式分解的是( )A、 B、 C、 D、7. 计算|﹣2|+2﹣1的结果是( )A、﹣1 B、0 C、1 D、28. 如图,点E在BC的延长线上,下列条件能判定AB∥CD的是( )
A、两点之间线段最短 B、点到直线的距离 C、两点确定一条直线 D、垂线段最短2. 如果 ,那么下列结论中一定成立的是( )A、 B、 C、 D、3. 下列运算正确的是( )A、(a2)3=a5 B、a8÷a4=a2 C、(a+b)2=a2+b2 D、(a﹣b)(a+b)=a2﹣b24. 把 写成 ( , 为整数)的形式,则 为( )A、 B、 C、 D、5. 方程2x+y=5与下列方程构成的方程组的解为 的是( )A、x﹣y=4 B、x+y=4 C、3x﹣y=8 D、x+2y=﹣16. 下列各式能用公式法因式分解的是( )A、 B、 C、 D、7. 计算|﹣2|+2﹣1的结果是( )A、﹣1 B、0 C、1 D、28. 如图,点E在BC的延长线上,下列条件能判定AB∥CD的是( )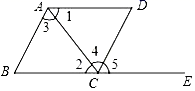 A、∠1=∠2 B、∠3=∠4 C、∠DAB+∠B=180° D、∠D=∠59. 不等式 的解集在数轴上表示正确的是( )A、
A、∠1=∠2 B、∠3=∠4 C、∠DAB+∠B=180° D、∠D=∠59. 不等式 的解集在数轴上表示正确的是( )A、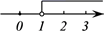 B、
B、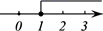 C、
C、 D、
D、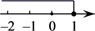 10. 下列条件能说明△ABC是直角三角形的是( )A、∠A=∠B=2∠C B、∠A=∠B+∠C C、∠A:∠B:∠C=2:3:4 D、∠A=40°,∠B=55°11. 若3x=4,3y=6,则3x+y的值是( )A、24 B、10 C、3 D、212. 如图,点D在△ABC内,且∠BDC=120°,∠1+∠2=55°,则∠A的度数为( )
10. 下列条件能说明△ABC是直角三角形的是( )A、∠A=∠B=2∠C B、∠A=∠B+∠C C、∠A:∠B:∠C=2:3:4 D、∠A=40°,∠B=55°11. 若3x=4,3y=6,则3x+y的值是( )A、24 B、10 C、3 D、212. 如图,点D在△ABC内,且∠BDC=120°,∠1+∠2=55°,则∠A的度数为( )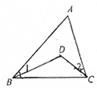 A、50° B、60° C、65° D、75°13. 如果 , ,且 、 是长方形的长和宽,则这个长方形的面积是( )A、3 B、4 C、5 D、614. 如图,△ABC的面积是1,AD是△ABC的中线,AF= FD,CE= EF,则△DEF的面积为( )
A、50° B、60° C、65° D、75°13. 如果 , ,且 、 是长方形的长和宽,则这个长方形的面积是( )A、3 B、4 C、5 D、614. 如图,△ABC的面积是1,AD是△ABC的中线,AF= FD,CE= EF,则△DEF的面积为( )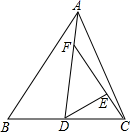 A、 B、 C、 D、15. 若关于 的不等式组 无解,则 的取值范围是( )A、 B、 C、 D、16. 如图,将一张三角形纸片ABC的三角折叠,使点A落在△ABC的A′处折痕为DE,若∠A=α,∠CEA′=β,∠BDA′=γ,那么下列式子中正确的是( )
A、 B、 C、 D、15. 若关于 的不等式组 无解,则 的取值范围是( )A、 B、 C、 D、16. 如图,将一张三角形纸片ABC的三角折叠,使点A落在△ABC的A′处折痕为DE,若∠A=α,∠CEA′=β,∠BDA′=γ,那么下列式子中正确的是( )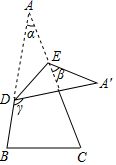 A、γ=180°﹣α﹣β B、γ=α+2β C、γ=2α+β D、γ=α+β
A、γ=180°﹣α﹣β B、γ=α+2β C、γ=2α+β D、γ=α+β二、填空题
-
17. 多项式 的公因式是 .18. 已知三角形的两边长分别为2和7,则第三边x的范围是 .19. 如图 , ,则 的度数为 .
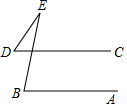 20. 对于有理数 ,我们规定 表示不大于 的最大整数,例如: , , ,若 ,则整数x的取值是 .
20. 对于有理数 ,我们规定 表示不大于 的最大整数,例如: , , ,若 ,则整数x的取值是 .三、解答题
-
21. 解不等式 .
请结合题意填空,完成本题的解答
(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来;(4)、原不等式组的解集为 .22. 一次课堂练习,小红做了如下四道因式分解题:① ;② ;③ ;④(1)、小红做错的或不完整的题目是(填序号);(2)、把(1)题中题目的正确答案写在下面.23. 如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,点F为AC延长线上的一点,连接DF.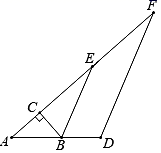 (1)、求∠CBE的度数;(2)、若∠F=25°,求证:BE∥DF.24. 整式的乘法与因式分解是有理数运算的自然延伸,也是代数知识的基本内容,请利用相关知识解决下面的问题:(1)、化简计算:(n+2)(4n﹣8)+17;(2)、在(1)题结果的基础上,增加一个单项式,使新得到的多项式能运用完全平方公式进行因式分解,请写出所有这样的单项式,并进行因式分解;(3)、试说明两个连续奇数的平方差能够被8整除.25. 好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决.如图,在△ABC中,∠BAC=48°,点I是两角∠ABC、∠ACB的平分线的交点.
(1)、求∠CBE的度数;(2)、若∠F=25°,求证:BE∥DF.24. 整式的乘法与因式分解是有理数运算的自然延伸,也是代数知识的基本内容,请利用相关知识解决下面的问题:(1)、化简计算:(n+2)(4n﹣8)+17;(2)、在(1)题结果的基础上,增加一个单项式,使新得到的多项式能运用完全平方公式进行因式分解,请写出所有这样的单项式,并进行因式分解;(3)、试说明两个连续奇数的平方差能够被8整除.25. 好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决.如图,在△ABC中,∠BAC=48°,点I是两角∠ABC、∠ACB的平分线的交点.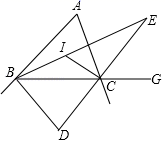 (1)、填空:∠BIC= .(2)、若点D是两条外角平分线的交点,填空:∠BDC= .(3)、若点E是内角∠ABC、外角∠ACG的平分线的交点,填空:∠BEC= .(4)、在问题(3)的条件下,当∠ACB等于度时,CE∥AB?请说明理由.26. 有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为255人,1辆甲种客车与2辆乙种客车的总载客量为150人.(1)、请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?(2)、某学校组织460名师生集体外出活动,拟租用甲、乙两种客车共8辆,一次将全部师生送到指定地点,至少需要租甲种客车几辆?
(1)、填空:∠BIC= .(2)、若点D是两条外角平分线的交点,填空:∠BDC= .(3)、若点E是内角∠ABC、外角∠ACG的平分线的交点,填空:∠BEC= .(4)、在问题(3)的条件下,当∠ACB等于度时,CE∥AB?请说明理由.26. 有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为255人,1辆甲种客车与2辆乙种客车的总载客量为150人.(1)、请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?(2)、某学校组织460名师生集体外出活动,拟租用甲、乙两种客车共8辆,一次将全部师生送到指定地点,至少需要租甲种客车几辆?