广东省珠海市香洲区2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-09-01 类型:期末考试
一、单选题
-
1. 4的算术平方根是( )A、-2 B、2 C、 D、2. 下列图形中,∠1与∠2互为邻补角的是( )A、
 B、
B、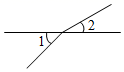 C、
C、 D、
D、 3. 下列各数中是无理数的是( )A、 B、 C、 D、3.144. 在下列调查中,适宜采用全面调查的是( )A、了解某省中学生的视力情况 B、了解某班学生的身高情况 C、检测一批电灯泡的使用寿命 D、调查一批汽车的抗撞击能力5. 在乡村振兴活动中,某村通过铺设水管将河水引到村庄C处,为节省材料,他们过点C向河岸l作垂线,垂足为点D,于是确定沿CD铺设水管,这样做的数学道理是( )
3. 下列各数中是无理数的是( )A、 B、 C、 D、3.144. 在下列调查中,适宜采用全面调查的是( )A、了解某省中学生的视力情况 B、了解某班学生的身高情况 C、检测一批电灯泡的使用寿命 D、调查一批汽车的抗撞击能力5. 在乡村振兴活动中,某村通过铺设水管将河水引到村庄C处,为节省材料,他们过点C向河岸l作垂线,垂足为点D,于是确定沿CD铺设水管,这样做的数学道理是( )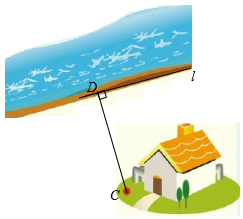 A、两点之间,线段最短 B、过一点有且只有一条直线与已知直线垂直 C、垂线段最短 D、两条直线相交有且只有一个交点6. 第三象限内的点P到x轴的距离是 ,到y轴的距离是 ,那么点P的坐标是( )A、 B、 C、 D、7. 李老师设计了一个关于实数运算的程序:输入一个数,乘以 后再减去 ,输出结果.若小刚按程序输入2,则输出的结果应为( )A、2 B、 C、﹣ D、38. 下列语句中,是真命题的是( )A、如果|a|=|b|,那么a=b B、一个正数的平方大于这个正数 C、内错角相等,两直线平行 D、如果a>b,那么ac>bc9. 若a﹣b<0,则下列不等式正确的是( )A、3a>3b B、﹣2a>﹣2b C、a﹣1>b﹣1 D、3﹣a<3﹣b10. 已知关于x,y的二元一次方程组 ,下列结论中正确的是( )
A、两点之间,线段最短 B、过一点有且只有一条直线与已知直线垂直 C、垂线段最短 D、两条直线相交有且只有一个交点6. 第三象限内的点P到x轴的距离是 ,到y轴的距离是 ,那么点P的坐标是( )A、 B、 C、 D、7. 李老师设计了一个关于实数运算的程序:输入一个数,乘以 后再减去 ,输出结果.若小刚按程序输入2,则输出的结果应为( )A、2 B、 C、﹣ D、38. 下列语句中,是真命题的是( )A、如果|a|=|b|,那么a=b B、一个正数的平方大于这个正数 C、内错角相等,两直线平行 D、如果a>b,那么ac>bc9. 若a﹣b<0,则下列不等式正确的是( )A、3a>3b B、﹣2a>﹣2b C、a﹣1>b﹣1 D、3﹣a<3﹣b10. 已知关于x,y的二元一次方程组 ,下列结论中正确的是( )①当这个方程组的解x,y的值互为相反数时,a=﹣1;
②当x为正数,y为非负数时,﹣ <a≤ ;
③无论a取何值,x+2y的值始终不变.
A、①② B、②③ C、①③ D、①②③二、填空题
-
11. 计算: .12. 在平面直角坐标系中,将点A(3,m﹣2)在x轴上,则m= .13. 根据如表数据回答259.21的平方根是 .
x
16
16.1
16.2
16.3
x2
256
259.21
262.44
265.69
14. 已知二元一次方程2x﹣3y﹣5=0的一组解为 ,则2a﹣3b+3= .15. 某次知识竞赛共有 20 题,每一题答对得 10 分,答错或不答都扣 5 分,小明想得分不少 于 90 分,他至少要答对题.16. 如图,将长方形ABCD沿对角线AC折叠,使点B落在点E处,AE交CD于点F.若∠EFC=70°,则∠ACF=°. 17. 为组织研学活动,王老师把班级里50名学生计划分成若干小组,若每组只能是4人或5人,则有 种分组方案.
17. 为组织研学活动,王老师把班级里50名学生计划分成若干小组,若每组只能是4人或5人,则有 种分组方案.三、解答题
-
18. 在等式y=kx+b中,当x=3时,y=3;当x=﹣1时,y=1.求k,b的值.19. 解不等式组 ,并将不等式组的解集在数轴上表示出来.20. 在平面直角坐标系中,点P(﹣5,2)和点Q(m+1,3m﹣1),当线段PQ与x轴平行时,求线段PQ的长.21. 某校为了解学生的体育锻炼情况,围绕“你最喜欢的一项体育活动”进行随机抽样调查,从而得到一组数据,如图是根据这组数据绘制的两个统计图.

请结合统计图,解答下列问题:
(1)、该校对名学生进行了抽样调查:在扇形统计图中,“羽毛球”所对应的圆心角的度数为度;(2)、补全条形统计图;(3)、若该校共有2400名学生,请你估计全校学生中最喜欢跳绳活动的人数约为多少人.22. 如图,DE⊥AC,FG⊥AC,∠1=∠2,∠B=∠3+50°,∠CAB=60°. (1)、求证:BC∥AG;(2)、求∠C的度数.23. 为鼓励市民节约用电,某市对居民用电实行“阶梯收费”(总电费=第一阶梯电费+第二阶梯电费),规定:用电量不超过200度按第一阶梯电价收费,超过200度的部分按第二阶梯电价收费,如图是刘哲鹭家2019年2月和3月所交电费的收据(度数均取整数).
(1)、求证:BC∥AG;(2)、求∠C的度数.23. 为鼓励市民节约用电,某市对居民用电实行“阶梯收费”(总电费=第一阶梯电费+第二阶梯电费),规定:用电量不超过200度按第一阶梯电价收费,超过200度的部分按第二阶梯电价收费,如图是刘哲鹭家2019年2月和3月所交电费的收据(度数均取整数). (1)、该市规定的第一阶梯电费和第二阶梯电费单价分别为多少?(2)、刘鹭家4月份家庭支出计划中电费不超过120元,她家最大用电量为多少度?24. 小明同学在数学活动中,将一副三角板按如图1所示的方式放置,其中点B在线段EC上,点D在线段AC上,AB与DE相交于点F,∠C=90°,∠A=30°,∠E=45°.
(1)、该市规定的第一阶梯电费和第二阶梯电费单价分别为多少?(2)、刘鹭家4月份家庭支出计划中电费不超过120元,她家最大用电量为多少度?24. 小明同学在数学活动中,将一副三角板按如图1所示的方式放置,其中点B在线段EC上,点D在线段AC上,AB与DE相交于点F,∠C=90°,∠A=30°,∠E=45°.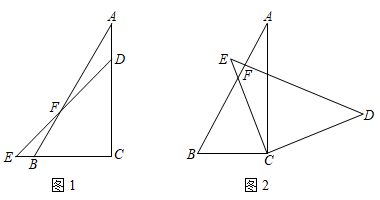 (1)、求∠BFD的度数;(2)、如图2,当小明将三角板DCE绕点C转动到ED⊥AB时,求∠BCE的度数;(3)、小明思考:在转动三角板DCE的过程中,当0°<∠BCE<180°,且点E在直线BC的上方时,是否存在DE与三角板ABC的一条边互相平行?若存在,请你帮小明直接写出∠BCE所有可能的值;若不存在,请说明理由25. 如图,在平面直角坐标系中,正方形ABCO的边长为1,边AO,CO分别在坐标轴的正半轴上,连接OB,以点O为圆心,对角线OB为半径画弧交x轴的正半轴于点D.
(1)、求∠BFD的度数;(2)、如图2,当小明将三角板DCE绕点C转动到ED⊥AB时,求∠BCE的度数;(3)、小明思考:在转动三角板DCE的过程中,当0°<∠BCE<180°,且点E在直线BC的上方时,是否存在DE与三角板ABC的一条边互相平行?若存在,请你帮小明直接写出∠BCE所有可能的值;若不存在,请说明理由25. 如图,在平面直角坐标系中,正方形ABCO的边长为1,边AO,CO分别在坐标轴的正半轴上,连接OB,以点O为圆心,对角线OB为半径画弧交x轴的正半轴于点D. (1)、填空:线段OB的长为 , 点D的坐标为;(2)、将线段AD向左平移到A′D′位置,当OA'=AD′时,求点D′的坐标;(3)、在(2)的条件下,求点D′到直线OB的距离.
(1)、填空:线段OB的长为 , 点D的坐标为;(2)、将线段AD向左平移到A′D′位置,当OA'=AD′时,求点D′的坐标;(3)、在(2)的条件下,求点D′到直线OB的距离.