广东省清远市2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-09-01 类型:期末考试
一、单选题
-
1. 下列图形是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件中,属于不可能事件的是( )A、投一次骰子,向上一面的点数是6 B、明天太阳从西边升起 C、射击运动员射击一次,命中靶心 D、经过有交通信号灯的路口,遇到红灯3. 下列计算正确的是( )A、(a+3)(a﹣2)=a2﹣6 B、(a﹣b)2=a2﹣b2 C、(﹣2a2)3=8a6 D、4a4÷2a3=2a4. 若一个三角形的两个内角的度数分别为30°和80°,则这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定5. 2020年6月23日,中国第55颗北斗导航卫星成功发射,顺利完成全球组网.其中支持北斗三号新信号的22纳米工艺射频基带一体化导航定位芯片,已实现规模化应用.22纳米=0.000000022米,将0.000000022用科学记数法表示为( )A、2.2×108 B、0.22×10﹣7 C、2.2×10﹣8 D、2.2×10﹣96. 如图,在△ABC中,∠ACB的平分线交AB于点D,过点D作DE∥BC交AC于点E,若∠AED=80°,则∠CDE的度数为( )
2. 下列事件中,属于不可能事件的是( )A、投一次骰子,向上一面的点数是6 B、明天太阳从西边升起 C、射击运动员射击一次,命中靶心 D、经过有交通信号灯的路口,遇到红灯3. 下列计算正确的是( )A、(a+3)(a﹣2)=a2﹣6 B、(a﹣b)2=a2﹣b2 C、(﹣2a2)3=8a6 D、4a4÷2a3=2a4. 若一个三角形的两个内角的度数分别为30°和80°,则这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定5. 2020年6月23日,中国第55颗北斗导航卫星成功发射,顺利完成全球组网.其中支持北斗三号新信号的22纳米工艺射频基带一体化导航定位芯片,已实现规模化应用.22纳米=0.000000022米,将0.000000022用科学记数法表示为( )A、2.2×108 B、0.22×10﹣7 C、2.2×10﹣8 D、2.2×10﹣96. 如图,在△ABC中,∠ACB的平分线交AB于点D,过点D作DE∥BC交AC于点E,若∠AED=80°,则∠CDE的度数为( ) A、30° B、40° C、60° D、80°7. 如图,在△ABC中,AB=AC,则添加下列条件后仍不能判定△ABE≌△ACD的是( )
A、30° B、40° C、60° D、80°7. 如图,在△ABC中,AB=AC,则添加下列条件后仍不能判定△ABE≌△ACD的是( ) A、BD=CE B、AD=AE C、∠B=∠C D、∠BAD=∠CAE8. 五一期间,小东家驾车去广东省博物馆参观,汽车从家里出发,匀速行驶段时间后,途中遇到堵车原地等待一会儿,由于路上车流量大,后面低速行驶到达广东省博物馆.参观一段时间后,驾车匀速返回家其中x表示小东一家从家甲出发后至回到家所用的时间,y表示汽车离家的距离,下面能反映y与x的函数关系的大致图象是( )A、
A、BD=CE B、AD=AE C、∠B=∠C D、∠BAD=∠CAE8. 五一期间,小东家驾车去广东省博物馆参观,汽车从家里出发,匀速行驶段时间后,途中遇到堵车原地等待一会儿,由于路上车流量大,后面低速行驶到达广东省博物馆.参观一段时间后,驾车匀速返回家其中x表示小东一家从家甲出发后至回到家所用的时间,y表示汽车离家的距离,下面能反映y与x的函数关系的大致图象是( )A、 B、
B、 C、
C、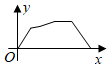 D、
D、 9. 如图,将直尺与含45°角的三角尺叠放在一起,其两边与直尺相交,若∠1=25°,则∠2的度数为( )
9. 如图,将直尺与含45°角的三角尺叠放在一起,其两边与直尺相交,若∠1=25°,则∠2的度数为( ) A、120° B、135° C、150° D、160°10. 如图,在△ABC中,点D是BC上一点,连接AD,将△ACD沿AD折叠至△AC'D,若∠B=30°,∠C=50°,∠CAD=60°,则∠C'AB的度数为( )
A、120° B、135° C、150° D、160°10. 如图,在△ABC中,点D是BC上一点,连接AD,将△ACD沿AD折叠至△AC'D,若∠B=30°,∠C=50°,∠CAD=60°,则∠C'AB的度数为( ) A、20° B、30° C、35° D、40
A、20° B、30° C、35° D、40二、填空题
-
11. 计算 .12. 如图,是去年黄瓜的销售价格y(元/千克)随月份x(月)变化的图象.请根据图象描述黄瓜价格最低是 月.
 13. 如图,MN∥CD,点A,B在直线MN上,连接AD,BC交于点O,若∠C=30°,∠MAD=140°,则∠AOB= .
13. 如图,MN∥CD,点A,B在直线MN上,连接AD,BC交于点O,若∠C=30°,∠MAD=140°,则∠AOB= . 14. “四时花竞巧,九子粽争新”,端午节吃粽子是我国的传统习俗.小佩的妈妈准备了形状大小一样的豆沙粽3个、红枣粽4个、腊肉粽2个,板栗粽3个,其中腊肉粽是咸粽,其它粽是甜粽.小佩随机选一个,选到咸粽的概率是 .15. 如图,在△ABC中,∠C=90°,点D是边BC上一动点,若AC=4,BC=15,CD=x,则△ABD的面积S与x之间的函数关系式为 .
14. “四时花竞巧,九子粽争新”,端午节吃粽子是我国的传统习俗.小佩的妈妈准备了形状大小一样的豆沙粽3个、红枣粽4个、腊肉粽2个,板栗粽3个,其中腊肉粽是咸粽,其它粽是甜粽.小佩随机选一个,选到咸粽的概率是 .15. 如图,在△ABC中,∠C=90°,点D是边BC上一动点,若AC=4,BC=15,CD=x,则△ABD的面积S与x之间的函数关系式为 . 16. 如图,在△ABC中,点D是边BC的中点,连接AD,取AD中点为E,连接CE、BE,取BE的中点F,连接CF,若△BCF的面积为6,则△ABC的面积为 .
16. 如图,在△ABC中,点D是边BC的中点,连接AD,取AD中点为E,连接CE、BE,取BE的中点F,连接CF,若△BCF的面积为6,则△ABC的面积为 . 17. 如图,在△ABC中,AP平分∠BAC交BC于点P,过点P作PR⊥AB垂足为R,PS⊥AC垂足为S,在AC上取一点Q,使AQ=PQ.则①PR=PS,②AS=AR,③QP∥AR,④△BRP≌△CSP.其中正确的有 . (填序号)
17. 如图,在△ABC中,AP平分∠BAC交BC于点P,过点P作PR⊥AB垂足为R,PS⊥AC垂足为S,在AC上取一点Q,使AQ=PQ.则①PR=PS,②AS=AR,③QP∥AR,④△BRP≌△CSP.其中正确的有 . (填序号)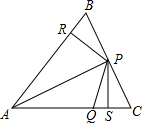
三、解答题
-
18. 计算:(π﹣2021)0+(﹣1)2021+( )﹣1 .19. 先化简,再求值:(x﹣2y)2﹣x(x﹣4y),其中,x=1,y=﹣2.20. 如图,点D、E、F分别为△ABC的边BC、CA、AB上的点,DE∥AB,∠A=∠EDF.那么∠C与∠BDF有什么关系?为什么?
 21. 如图,O是AB上一点,过点O作射线OC.
21. 如图,O是AB上一点,过点O作射线OC.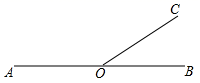 (1)、利用尺规作图分别作∠AOC和∠BOC的平分线OD,OE(保留作图痕迹,不写作法).(2)、试判断OD与OE的位置关系,并说明理由.22. 如图是小彬设计的一个圆形转盘转盘被均匀的分成8份,分别标有1、2、3、4、5、6、7、8这8个数,转动转盘,当转盘停止时,指针指向的数即为转出的数.(当指针恰好指在分界线上时,无效重转)
(1)、利用尺规作图分别作∠AOC和∠BOC的平分线OD,OE(保留作图痕迹,不写作法).(2)、试判断OD与OE的位置关系,并说明理由.22. 如图是小彬设计的一个圆形转盘转盘被均匀的分成8份,分别标有1、2、3、4、5、6、7、8这8个数,转动转盘,当转盘停止时,指针指向的数即为转出的数.(当指针恰好指在分界线上时,无效重转)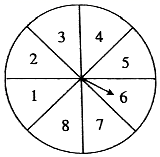 (1)、求小彬转出的数是3的倍数的概率.(2)、现有两张分别写有3和5的卡片,随机转动转盘,转盘停止后记下转出的数,与两张卡片上的数分别作为三条线段的长度.这三条线段能构成三角形的概率是多少?23. 如图所示的正方形网格中,△ABC的三个顶点都在格点上(即网格线的交点).
(1)、求小彬转出的数是3的倍数的概率.(2)、现有两张分别写有3和5的卡片,随机转动转盘,转盘停止后记下转出的数,与两张卡片上的数分别作为三条线段的长度.这三条线段能构成三角形的概率是多少?23. 如图所示的正方形网格中,△ABC的三个顶点都在格点上(即网格线的交点). (1)、请在网格平面内作出△ABC关于直线l对称的△A'B'C'.(2)、在直线l上作一点P,使PB+PC的值最小.24. 如图1,是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2).
(1)、请在网格平面内作出△ABC关于直线l对称的△A'B'C'.(2)、在直线l上作一点P,使PB+PC的值最小.24. 如图1,是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2). (1)、观察图2,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .(2)、若m+n=5,mn=6,求(m﹣n)2的值.(3)、若x满足(9﹣x)(x﹣4)=4,求(x﹣9)2+(4﹣x)2的值.25. 如图1,∠ABC=90°,FA⊥AB于点A,D是线段AB上的点,AD=BC,AF=BD.
(1)、观察图2,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .(2)、若m+n=5,mn=6,求(m﹣n)2的值.(3)、若x满足(9﹣x)(x﹣4)=4,求(x﹣9)2+(4﹣x)2的值.25. 如图1,∠ABC=90°,FA⊥AB于点A,D是线段AB上的点,AD=BC,AF=BD.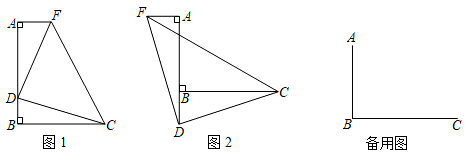 (1)、判断DF与DC的数量关系为 , 位置关系为 .(2)、如图2,若点D在线段AB的延长线上,过点A在AB的另一侧作AF⊥AB,并截取AF=BD,连接DC、DF、CF,试说明(1)中结论是否成立,并说明理由.(3)、若点D在线段AB外,点E是BC延长线上一点,且CE=BD,连接AE,与DC的延长线交于点P,直接写出∠APC的度数.
(1)、判断DF与DC的数量关系为 , 位置关系为 .(2)、如图2,若点D在线段AB的延长线上,过点A在AB的另一侧作AF⊥AB,并截取AF=BD,连接DC、DF、CF,试说明(1)中结论是否成立,并说明理由.(3)、若点D在线段AB外,点E是BC延长线上一点,且CE=BD,连接AE,与DC的延长线交于点P,直接写出∠APC的度数.