广东省江门市台山市2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-09-01 类型：期末考试

进入出卷网下载

一、单选题

1. 81的平方根为（）

A、9 B、±9 C、－9 D、±3

查看试题解析
2. 在坐标平面内，下列各点中到x轴的距离最近的点是（）

A、（2，5） B、（－4，1） C、（3，－4） D、（6，2）

查看试题解析
3. 如图，△ABC沿BC方向平移得到△DEF，已知BC=7，EC=4，那么平移的距离为（）

A、2 B、3 C、5 D、7

查看试题解析
4. 下列调查中，适合采用抽样调查的是（）

A、调查本班同学的视力 B、调查一批节能灯管的使用寿命 C、为保证“神舟十二号”的成功发射，对其零部件进行检查 D、对乘坐某班次客车的乘客进行安检

查看试题解析
5. 下列不等式的变形中，一定正确的是（）

A、若 $a c > b c$ ，则 $a > b$ B、若 $a > b$ ，则 $a m^{2} > b m^{2}$ C、若 $a c^{2} > b c^{2}$ ，则 $a > b$ D、若 $a > 0$ ， $b > 0$ ，且 $\frac{1}{a} > \frac{1}{b}$ ，则 $a > b$

查看试题解析
6. 已知关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} x - y = 6 \\ 2 x + y = m \end{array}$ 中， $x$ 与 $y$ 互为相反数，则 $m$ 的值是（）

A、0 B、 $- 3$ C、3 D、9

查看试题解析
7. 如图，下列条件中，不能判定 $A B // C D$ 的是（）

A、 $∠ D + ∠ B A D = 180 °$ B、 $∠ B A C = ∠ A C D$ C、 $∠ C A D = ∠ A C B$ D、 $∠ B = ∠ D C E$

查看试题解析
8. 化简 $| a - 2 | + {(\sqrt{2 - a})}^{2}$ 的结果是（）

A、 $4 - 2 a$ B、0 C、 $2 a - 4$ D、4

查看试题解析
9. 如图， $A B / / C D$ ，直线 $E F$ 分别交 $A B$ ， $C D$ 于点E，F， $E G$ 平分 $∠ B E F$ ，若 $∠ E F G = 64 °$ ，则 $∠ E G D$ 的大小是（）

A、 $132 °$ B、 $128 °$ C、 $122 °$ D、 $112 °$

查看试题解析
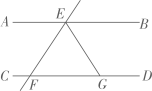10. 若关于x的一元一次不等式组 ${\begin{array}{l} x - a > 0 \\ 1 - 2 x > x - 2 \end{array}$ 无解，则a的取值范围是（）

A、 $a \geq 1$ B、 $a > 1$ C、 $a \leq - 1$ D、 $a < - 1$

查看试题解析

二、填空题

11. 若 $x^{3} = - 27$ ，则 $x =$ ．

查看试题解析
12. 若关于x的方程3x﹣kx+2＝0的解为2，则k的值为.

查看试题解析
13. 2019年4月29日中国北京世界园艺博览会在北京延庆开幕，大会以“绿色生活，美丽家园”为主题．如图，是北京世界园艺博览会部分导游图，若国际馆的坐标为（4，2），植物馆的坐标为（﹣4，﹣1），则中国馆的坐标为．

查看试题解析
14. 如图，已知 $B E$ 平分 $∠ A B C$ ，且 $B E // D C$ ，若 $∠ A B C = 60 °$ ，则 $∠ C$ 的度数是．

查看试题解析
15. 王玲和李凯进行投球比赛，每人连投12次，投中一次记2分，投空一次记1分，王玲先投，投得16分，李凯要想超过王玲，应至少投中次.

查看试题解析
16. 对于x，y定义一种新运算“ $*$ ”， $x y = a x + b y$ ，其中a，b是常数，等式右边是通常的加法和乘法运算．已知 $3 * 5 = 15$ ， $4 * 7 = 28$ ，则 $1 * 1$ 的值为．

查看试题解析
17. 如图， $A E // C F$ ， $∠ A C F$ 的平分线交 $A E$ 于点 $B$ ， $G$ 是 $C F$ 上的一点， $∠ G B E$ 的平分线交 $C F$ 于点 $D$ ，且 $B D ⊥ B C$ ，下列结论：① $B C$ 平分 $∠ A B G$ ；② $A C // B G$ ；③与 $∠ D B E$ 互余的角有2个；④若 $∠ A = α$ ，则 $∠ B D F = 108 ° - \frac{α}{8}$ ．其中正确的是（请把正确结论的序号都填上）

查看试题解析

三、解答题

18. 计算： $- \sqrt[3]{- 8} + \sqrt[3]{125} + \sqrt{{(- 2)}^{2}}$ ．

查看试题解析
19. 解方程组： ${\begin{array}{l} 2 (x - 1) = y + 5 \\ 5 y - 6 = 3 (x + 5) \end{array}$

查看试题解析
20. 解不等式组： ${\begin{array}{l} x - 3 (x - 2) ⩾ 4 \\ \frac{2 x - 1}{5} < \frac{x + 1}{2} \end{array}$ .

查看试题解析
21. 如图，AD∥EF，∠1+∠2＝180°，

(1)、求证：DG∥AB；

(2)、若DG是∠ADC的角平分线，∠1＝30°，求∠B的度数.

查看试题解析
22.
小明在学校组织的社会调查活动中负责了解他所居住的小区560户居民的家庭收入情况．他从中随机调查了一定户数的家庭收入情况（收入取整数，单位：元），并绘制了如下的频数分布表和频数分布直方图．
分组
频数
百分比
600≤x＜800
2
5%
800≤x＜1000
6
15%
1000≤x＜1200
a
40%
1200≤x＜1400
9
22.5%
1400≤x＜1600
b
c
1600≤x＜1800
2
5%
合计
40
100%

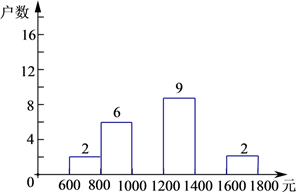
根据以上提供的信息，解答下列问题：

(1)、频数分布表中：a= ， b= ， c= ．

(2)、补全频数分布直方图．

(3)、请估计该居民小区家庭属于中等收入（大于1000不足1600元）的大约有多少户？

查看试题解析

23. 某地葡萄丰收，准备将已经采摘下来的11400公斤葡萄运送杭州，现有甲、乙、丙三种车型共选择，每辆车运载能力和运费如表表示（假设每辆车均满载）

车型	甲	乙	丙
汽车运载量（公斤/辆）	600	800	900
汽车运费（元/辆）	500	600	700

(1)、若全部葡萄都用甲、乙两种车型来运，需运费8700元，则需甲、乙两种车型各几辆？

(2)、为了节省运费，现打算用甲、乙、丙三种车型都参与运送，已知它们的总辆数为15辆，你能分别求出这三种车型的辆数吗？怎样安排运费最省？

查看试题解析

24. 如图，在平面直角坐标系中，点 $A$ ， $B$ 的坐标分别为 $(- 1 ， 0)$ 和 $(3 ， 0)$ ．现将线段 $A B$ 平移得到线段 $C D$ ，且点 $A$ 的对应点 $C$ 的坐标为 $(0 ， 2)$ ，连接 $A D$ ．

(1)、直接写出点 $D$ 的坐标为， $△ A B D$ 的面积为；

(2)、将线段 $A D$ 向左平移 $m$ 个单位，再向上平移 $n$ 个单位后得线段 $E F$ ，点 $A$ 的对应点 $E$ 的坐标为 $E (a ， b)$ ，点 $D$ 的对应点为 $F$ ，如果 $x = a$ ， $y = b$ 是方程 $2 x + y = - 3$ 的解，且点 $F$ 在第一象限的角平分线上，求 $a$ ， $b$ 的值．

(3)、点 $P (t ， 0)$ 是 $x$ 轴上位于点 $A$ 右侧的动点，连接 $P C$ ，将线段 $P C$ 向右平移得线段 $Q D$ ，其中点 $P$ 的对应点为 $Q$ ，点 $C$ 的对应点为 $D$ ， $H$ 是 $D Q$ 的中点，如果 $△ B D H$ 和三角形 $P B D$ 面积相等求 $t$ 的值．[参考公式：点 $P$ 的坐标 $(x_{1} ， y_{1})$ ，点 $Q$ 的坐标 $(x_{2} ， y_{2})$ ，则线段 $P Q$ 的中点 $M$ 的坐标为 $(\frac{x_{1} + x_{2}}{2} ， \frac{y_{1} + y_{2}}{2})$ ]

查看试题解析
25. 如图，已知 $A B // C D$ ， $C N$ 是 $∠ B C E$ 的平分线．

(1)、若 $C M$ 平分 $∠ B C D$ ，求 $∠ M C N$ 的度数；

(2)、若 $C M$ 在 $∠ B C D$ 的内部，且 $C M ⊥ C N$ 于 $C$ ，求证： $C M$ 平分 $∠ B C D$ ；

(3)、在（2）的条件下，过点 $B$ 作 $B P ⊥ B Q$ ，分别交 $C M$ 、 $C N$ 于点 $P$ 、 $Q$ ， $∠ P B Q$ 绕着 $B$ 点旋转，但与 $C M$ 、 $C N$ 始终有交点，问： $∠ B P C + ∠ B Q C$ 的值是否发生变化？若不变，求其值；若变化，求其变化范围．

查看试题解析

分组	频数	百分比
600≤x＜800	2	5%
800≤x＜1000	6	15%
1000≤x＜1200	a	40%
1200≤x＜1400	9	22.5%
1400≤x＜1600	b	c
1600≤x＜1800	2	5%
合计	40	100%