初中数学湘教版八年级上册4.5一元一次不等式组 同步练习
试卷更新日期:2021-08-31 类型:同步测试
一、单选题
-
1. 下列不等式组是一元一次不等式组的是( )A、 B、 C、 D、2. 关于 的不等式组 有解,那么 的取值范围为( )A、 B、 C、 D、3. 已知a , b为实数,则解是 的不等式组可以是( )A、 B、 C、 D、4. 若数m使关于x的一元一次不等式组 的解集是 ,且使关于y的分式方程 有非负整数解,则符合条件的所有整数m的值之和为( )A、-3 B、0 C、2 D、55. 若关于x的不等式组 的所有整数解的和为0,则m的值不可能是( )A、3 B、3.5 C、3.7 D、46. 若不等式组 有解,则a的取值范围是( ).A、 ≤-2 B、 ≥-2 C、 <-2 D、 >-27. 如图,数轴上表示的是下列哪个不等式组的解集( )
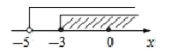 A、 B、 C、 D、8. 不等式组 的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、8. 不等式组 的解集在数轴上表示正确的是( )A、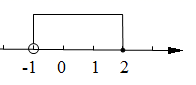 B、
B、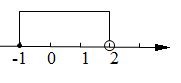 C、
C、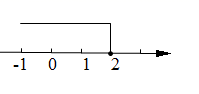 D、
D、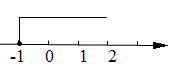 9. 已知关于 的不等式组 有解,则 的取值不可能是( )A、0 B、1 C、2 D、-210. 用若干量载重量为6吨的火车运一批货物,若每辆货车只装4吨,则剩下18吨货物;若每辆货车装6吨,则最后一辆车装的货物不足5吨,若设有 辆货车,则 应满足的不等式组是( )A、 B、 C、 D、
9. 已知关于 的不等式组 有解,则 的取值不可能是( )A、0 B、1 C、2 D、-210. 用若干量载重量为6吨的火车运一批货物,若每辆货车只装4吨,则剩下18吨货物;若每辆货车装6吨,则最后一辆车装的货物不足5吨,若设有 辆货车,则 应满足的不等式组是( )A、 B、 C、 D、二、填空题
-
11. 不等式组 解集是 .12. 不等式组 的最大整数解为 .13. 已知关于x的不等式组 ,其中m , n在数轴上的对应点如图所示 .
 14. 解不等式组 得 .15. 若关于 的不等式组 无解,则a的取值范围是 .16. 若关于x的不等式组 只有3个整数解,则m的取值范围是 .
14. 解不等式组 得 .15. 若关于 的不等式组 无解,则a的取值范围是 .16. 若关于x的不等式组 只有3个整数解,则m的取值范围是 .三、计算题
-
17. 解不等式组:18. 解不等式组:
四、解答题
-
19. 解不等式组 ,并写出它的非负整数解.20. 解不等式组: ,并写出不等式组的所有整数解.21. 某储运站现有甲种货物1530吨,乙种货物1150吨,安排用一列货车将这批货物运往青岛,这列货车可挂A,B两种不同规格的货厢50节.已知甲种货物35吨和乙种货物15吨可装满一节A型货厢,甲种货物25吨和乙种货物35吨可装满一节B型货厢,按此要求安排A,B两种货厢的节数,有哪几种运输方案?请设计出来.22. 解不等式组 ,并在数轴上表示解集.
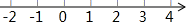
五、综合题
-
23. 阅读以下例题:解不等式:(x+4)(x-1)>0
解:①当x+4>0,则x-1>0
即可以写成:
解不等式组得:
②当若x+4<0,则x-1<0
即可以写成:
解不等式组得:
综合以上两种情况:不等式解集:x>1或 .
(以上解法依据:若ab>0,则a,b同号)请你模仿例题的解法,解不等式:
(1)、(x+1)(x-2)>0;(2)、(x+2)(x-3)<0.24. 为执行中央“节能减排,美化环境,建设美丽新农村”的国策,我市某村计划建造 两种型号的沼气池共20个,以解决该村所有农户的燃料问题,两种型号沼气池的占地面积、使用农户数及造价见下表:型号
占地面积( /个)
使用农户数(户/个)
造价(万元/个)
15
18
2
20
30
3
已知可供建造沼气池的占地面积不超过 ,该村农户共有492户.
(1)、满足条件的方案共有几种?写出解答过程;(2)、通过计算判断,哪种建造方案最省钱.25. 阅读下列材料:解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解:∵x﹣y=2,又∵x>1,∴y+2>1,即y>﹣1
又y<0,∴﹣1<y<0.…①
同理得:1<x<2.…②
由①+②得﹣1+1<y+x<0+2,∴x+y的取值范围是0<x+y<2.
请按照上述方法,完成下列问题:
已知关于x、y的方程组 的解都为非负数.
(1)、求a的取值范围;(2)、已知2a﹣b=1,且,求a+b的取值范围;
(3)、已知a﹣b=m(m是大于1的常数),且b≤1,求2a+b最大值.(用含m的代数式表示)