初中数学湘教版八年级上册4.2不等式的基本性质同步练习

试卷更新日期：2021-08-31 类型：同步测试

进入出卷网下载

一、单选题

1. 已知m＜n，下列不等式一定成立的是（）

A、3m＜3n B、m﹣6＞n﹣6 C、﹣2m＜﹣2n D、 $\frac{m}{2} > \frac{n}{2}$

查看试题解析
2. 下列不等式变形正确的是（）

A、由4x﹣1＞0得：4x＞1 B、由5x＞3得：x＞3 C、由 $\frac{y}{2}$ ＞0得：y＜0 D、由﹣2x＜4得：x＜﹣2

查看试题解析
3. 若 $x > y$ ，则下列式子中正确的是（）．

A、 $x - 3 > y - 3$ B、 $x + 4 < y + 4$ C、 $- 5 x > - 5 y$ D、 $\frac{x}{2} < \frac{y}{2}$

查看试题解析
4. 已知a、b、c均为实数，若a＞b，c≠0，下列结论不一定正确的是（）

A、a＋c＞b＋c B、c－a＜c－b C、 $\frac{a}{c^{2}} > \frac{b}{c^{2}}$ D、a²＞ab＞b²

查看试题解析
5. 下列不等式变形正确的是（）

A、由 $a > b$ ，得 $a - 2 < b - 2$ B、由 $a > b$ ，得 $- 2 a < - 2 b$ C、由 $a > b$ ，得 $| a | > | b |$ D、由 $a > b$ ，得 $a^{2} > b^{2}$

查看试题解析
6. 若x+2021>y+2021，则（）

A、x+2<y+2 B、x－2<y－2 C、2x<2y D、－2x<－2y

查看试题解析
7. 若 $x < y$ ，则 $m x > m y$ 成立的条件是（）

A、 $m \geq 0$ B、 $m \leq 0$ C、 $m > 0$ D、 $m < 0$

查看试题解析
8. 若m>n，则不论a取何实数，下列不等式都成立的是（）

A、m+a>n B、ma>na C、a-m<a-n D、 $m a^{2} > n a^{2}$

查看试题解析
9. 下列叙述①若a>b，则ac²>bc²；②若a<b，则a-c<b-c；③若-3a>2a，则a<0④若ab>c，则b> $\frac{c}{a}$ 。其中正确的是（）

A、③④ B、①③ C、①② D、②③

查看试题解析
10. 下列不等式变形中，一定正确的是（）

A、若ac＞bc，则a＞b B、若a＞b，则am²＞bm² C、若ac²＞bc² ，则a＞b D、若m＞n，则﹣ $\frac{m}{2} > - \frac{n}{2}$

查看试题解析

二、填空题

11. 已知a＞b，则15a+c15b+c（填“＞”“＜”或“＝”）.

查看试题解析
12. 若a＞b，要使ac＜bc，则c0．

查看试题解析
13. 若 $a < b < 0$ ，则 $a b$ $a^{2}$ ．

查看试题解析
14. 根据不等式的基本性质，可将“mx＜2”化为“x＞ $\frac{2}{m}$ ”，则m的取值范围是.

查看试题解析
15. 如果0<a<1，那么a，1和 $\frac{1}{a}$ 的大小关系（用“<”连接）是．

查看试题解析

三、计算题

16. 利用不等式的基本性质，将下列不等式化为 $x > a$ 或 $x < a$ 的形式：

(1)、 $3 x > - 5$ ；

(2)、 $\frac{2}{3} x > 6 - \frac{1}{3} x$ .

查看试题解析
17. 若2a+b=12，其中a≥0，b≥0，又P=3a+2b．试确定P的最小值和最大值．

查看试题解析

四、解答题

18. 某数学兴趣小组在学习“不等式的性质”时，有两名同学的对话如下：

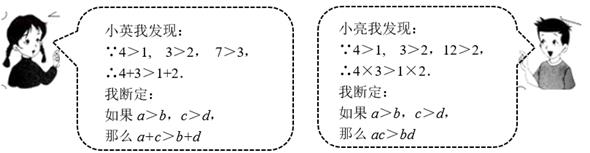
你认为小英和小亮的结论正确吗？如果正确，请说明理由；如果不正确，请举出一个反例。

查看试题解析
19. 依据不等式的性质，把下列不等式化成x>a或x<a的形式：

(1)、x+3<5

(2)、x- $\frac{4}{5}$ > $\frac{1}{5}$

查看试题解析

五、综合题

20. 已知x>y，比较下列式子的大小，并说明理由。

(1)、2x+1>2y+1；

(2)、5-2x<5-2y

查看试题解析
21. 我们知道不等式的两边加（或减）同一个数（或式子），不等号的方向不变，不等式组是否也具有类似的性质呢？请解答下列问题

(1)、完成下列填空：

已知

用“＜”或“＞”填空

${\begin{matrix} 4 > 3 \\ 2 > 1 \end{matrix}$

4+23+1

${\begin{matrix} - 3 < 2 \\ - 2 < - 1 \end{matrix}$

﹣3﹣22﹣1

(2)、一般地，如果 ${\begin{matrix} a < b \\ c < d \end{matrix}$ 那么a+cb+d（用“＜”或“＞”填空）请你利用不等式的基本性质说明上述不等式的正确性．

查看试题解析
22. 根据等式和不等式的基本性质，我们可以得到比较两数大小的方法：

(1)、若a－b＞0，则ab；

(2)、若a－b＝0，则ab；

(3)、若a－b＜0，则ab.

(4)、这种比较大小的方法称为“求差法比较大小”.
请运用这种方法尝试解决下面的问题：

比较4＋3a²－2b＋b²与3a²－2b＋1的大小.

查看试题解析

已知	用“＜”或“＞”填空
${\begin{matrix} 4 > 3 \\ 2 > 1 \end{matrix}$	4+23+1
${\begin{matrix} - 3 < 2 \\ - 2 < - 1 \end{matrix}$	﹣3﹣22﹣1

初中数学湘教版八年级上册4.2不等式的基本性质 同步练习

一、单选题

二、填空题

三、计算题

四、解答题

五、综合题

初中数学湘教版八年级上册4.2不等式的基本性质同步练习