广东省广州市荔湾区2020-2021学年高二下学期数学期末考试试卷

试卷更新日期：2021-08-31 类型：期末考试

进入出卷网下载

一、单选题

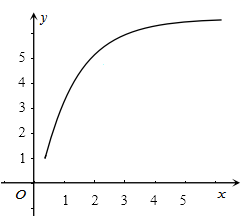
1. 复数 $z = \frac{1 - i}{i}$ （其中 $i$ 是虚数单位）的虚部是（）.

A、1 B、 $i$ C、-1 D、 $- i$

查看试题解析
2. 下列求导运算正确的是（）

A、 ${(x^{2} + \ln 2)}^{'} = 2 x + \frac{1}{2}$ B、 ${(\cos x^{2})}^{'} = - \sin x^{2}$ C、 ${(\frac{\ln x}{x})}^{'} = \frac{1 - \ln x}{x^{2}}$ D、 $(\sqrt{x + 1})^{'} = \frac{2}{\sqrt{x + 1}}$

查看试题解析
3. 函数 $f (x)$ 的图象如图所示，则下列数值排序正确的是（）

A、 $0 < f^{'} (2) < f^{'} (3) < f (3) - f (2)$ B、 $0 < f^{'} (3) < f (3) - f (2) < f^{'} (2)$ C、 $0 < f^{'} (3) < f^{'} (2) < f (3) - f (2)$ D、 $0 < f (3) - f (2) < f^{'} (2) < f^{'} (3)$

查看试题解析
4. A，B，C，D，E五人并排站成一排，如果A，B必须相邻且B在A的左边，那么不同的排法共有（）

A、60种 B、48种 C、36种 D、24种

查看试题解析
5. 甲、乙、丙、丁和戊5名学生进行劳动技术比赛，决出第1名到第5名的名次．甲、乙两名参赛者去询问成绩，回答者对甲说“很遗憾，你和乙都没有得到冠军”；对乙说“你当然不会是最差的”．从上述回答分析，5人的名次排列有（）种不同情况

A、36 B、54 C、72 D、81

查看试题解析
6. 用指数模型 $y = c e^{k x}$ 去拟合一组数据时，为了求出回归方程，设z＝㏑y，变换后得到线性回归直线方程 $z = 0.3 x + 4$ ，则常数 $c$ 的值为（）

A、 $e^{4}$ B、 $e^{0.3}$ C、0.3 D、4

查看试题解析
7. 甲、乙两队进行篮球决赛，采取五场三胜制（当一队得三场胜利时，该队获胜，比赛结束），根据前期比赛成绩，甲队的主客场安排依次为“主主客客主”．设甲队主场取胜的概率为0.6，客场取胜的概率为0.5；且各场比赛结果相互独立，则甲队以3∶1获胜的概率是（）

A、0.18 B、0.21 C、0.39 D、0.42

查看试题解析
8. 若 $x_{2} > x_{1} > 1$ ，则（）

A、 $e^{x_{2}} - e^{x_{1}} > 3 \ln x_{2} - 3 \ln x_{1}$ B、 $e^{x_{2}} - e^{x_{1}} < 3 \ln x_{2} - 3 \ln x_{1}$ C、 $x_{2} e^{x_{1}} < x_{1} e^{x_{2}}$ D、 $x_{2} e^{x_{1}} > x_{1} e^{x_{2}}$

查看试题解析

二、多选题

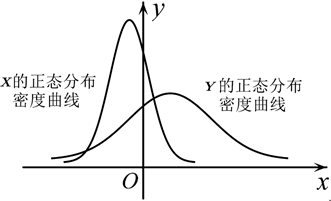
9. 下列叙述正确的是（）

A、回归直线一定过样本点的中心 $(\bar{x} ， \bar{y})$ B、在回归分析中， $R^{2} = 0.80$ 的模型比 $R^{2} = 0.98$ 的模型拟合的效果好 C、在残差图中，残差点分布的水平带状区域越窄，说明模型的拟合效果越好 D、某同学研究卖出的热饮杯数y与气温x（℃）的关系，得到回归方程 $\hat{y} = - 2.35 x + 146.7$ ，则气温为2℃时，一定可卖出142杯热饮

查看试题解析
10. 已知两种不同型号的电子元件（分别记为X，Y）的使用寿命均服从正态分布 $X \sim N (μ_{1} ， σ_{1}^{2}) ， Y \sim N (μ_{2} ， σ_{2}^{2})$ ，这两个正态分布密度曲线如图所示，下列结论中正确的是（）
（参考数据：若 $Z \sim N (μ ， σ^{2})$ ，则 $P (μ - σ \leq Z \leq μ + σ) \approx 0.6827 ， P (μ - 2 σ \leq Z \leq μ + 2 σ) \approx 0.9545$ ）

A、 $μ_{1} > μ_{2}$ B、 $σ_{1} < σ_{2}$ C、 $P (Y \geq μ_{2}) < P (Y \geq μ_{1})$ D、 $P (μ_{1} - σ_{1} \leq X \leq μ_{1} + 2 σ_{1}) \approx 0.8186$

查看试题解析
11. 在复平面内，复数z＝a＋bi对应向量为 $\vec{O Z}$ （O为坐标原点， $a ， b \in R$ ）．设 $| \vec{O Z} | = r$ ，射线Ox为始边，OZ为终边逆时针旋转的角为 $θ$ ，则 $z = r (\cos θ + i \sin θ)$ ．数学家棣莫弗发现：设 $z_{1} = r_{1} (\cos θ_{1} + i \sin θ_{1}) ， z_{2} = r_{2} (\cos θ_{2} + i \sin θ_{2})$ ，则 $z_{1} z_{2} = r_{1} r_{2} [\cos (θ_{1} + θ_{2}) + i \sin (θ_{1} + θ_{2}]$ ，我们称这个结论为英弗定理，并由此定理推出了复数乘方公式： $z^{n} = {[r (\cos θ + i \sin θ)]}^{n} = r^{n} (\cos n θ + i \sin n θ) (n \in N^{*})$ ，根据以上信息，下列说法正确的是（）

A、当r＝1， $θ = \frac{π}{3}$ 时， $z^{3} = 1$ B、当r＝1， $θ = \frac{π}{3}$ 时， $\bar{z} = \frac{1}{2} - \frac{\sqrt{3}}{2} i$ C、 $| z^{2} | = | z |^{2}$ D、当r＝1， $θ = \frac{π}{4}$ 时，若n为偶数，则复数 $z^{n}$ 为纯虚数

查看试题解析
12. 若函数 $f (x) = {\begin{matrix} 2 x^{2} \ln x ， x > 0 \\ - x^{3} - 4 x^{2} ， x \leq 0 \end{matrix}$ 的图像和直线y＝ax有四个不同的交点，则实数a的取值可以是（）

A、4 B、2 C、0 D、 $- \frac{1}{e}$

查看试题解析

三、填空题

13. 曲线 $y = x^{2} - x$ 在点P（－1，2）处的切线方程为．

查看试题解析
14. 新型冠状病毒疫情期间，4位志愿者需要被安排到3个不同的路口执勤，每个路口至少安排一人，总共有种不同安排方法．（用数字作答）

查看试题解析
15. ${(1 + 3 x)}^{6} {(1 - x)}^{3}$ 的展开式中x²的系数为．

查看试题解析
16. 某制造商制造并出售球型瓶装的某种饮料．每个瓶子的制造成本是 $0.8 π r^{2}$ 分，其中r（单位：cm）是瓶子的半径．已知每出售1mL的饮料，制造商可获利0.2分，且制造商能制作的瓶子的最大半径为6cm，当瓶子的半径r＝cm时，每瓶饮料的利润最大，最大值为分（结果保留 $π$ ）．

查看试题解析

四、解答题

17. 已知二项式 ${(1 - 2 x)}^{n}$ ，若选条件（填写序号），

(1)、求展开式中含 $x^{3}$ 的项；

(2)、设 ${(1 - 2 x)}^{n} = a_{0} + a_{1} x + a_{2} x^{2} + \dots + a_{n} x^{n}$ ，求展开式中奇次项的系数和．
请在：①只有第4项的二项式系数最大；②第2项与第6项的二项式系数相等；③所有二项式系数的和为64

这三个条件中任选一个，补充在上面问题中的线上，并完成解答．

注：如果选择多个条件分别解答，按第一个解答计分．

查看试题解析
18. 已知函数 $f (x) = x^{3} + a x^{2} + b x + 2$ ，f(x)的极值点分别为 $x_{1} = - 1 ， x_{2} = 3$ ．

(1)、求a，b的值；

(2)、求函数 $f (x)$ 的极值．

查看试题解析
19. 一个箱子中装有4个红球和3个白球，那么

(1)、一次取出2个球，在已知它们颜色相同的情况下，求该颜色是红色的慨率；

(2)、一次取出1个球，取出后记录颜色并放回箱中，取球3次，求取到红球个数X的期望与方差．

查看试题解析

20. 为响应“没有全民健康，就没有全面小康”的号召，社区开展了“健康身体，从我做起”社区健身活动，活动分为徒手运动和器械运动两大类，该社区对所有参与活的1000人进行了调查．其中男性600人中有180人参加徒手运动，女性中有320人参加器械运动．

(1)、根据以上提供的信息，完成2×2列联表，并回答能否在犯错误的概率不超过0.005的前提下认为选择器械运动与性别有关系？

	器械运动	徒手运动	总计
男性
女性
总计

(2)、将上述调查所得的频率视为概率，为了进一步弄清选徒手运动的影响因素，准备进行抽样调查，现从选徒手运动的人中按分层抽样的方法抽取13人，再从这13人中任意抽取3人进行访谈，记抽取3人中参加徒手运动的女性人数为与

ξ

，求

ξ

的概率分布列．

附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$

临界值表：

P（K²≥k₀）	0.10	0.05	0.010	0.005	0.001
k₀	2.706	3.841	6.635	7.879	10.828

查看试题解析

21. 某地位于甲、乙两条河流的交汇处，夏季多雨，根据统计资料预测，今年汛期甲河流发生洪水的概率为0.25，乙河流发生洪水的概率为0.2，（假设两河流发生洪水与否互不影响），现有一台大型设备正在该地施工，为了保护设备，施工方提出以下三种方案：
方案一：运走设备需要花费5000元；

方案二：建防洪设施，需要花费2000元，但防洪设施只能抵御一条河流发生的洪水，当两河流同时发生洪水时，设备将受损，损失56000元；

方案三：不采取措施，当两条河流同时发生洪水时损失60000元，只有一条河流发生洪水时，损失10000元．

(1)、求今年甲、乙两河流至少有一条发生洪水的概率；

(2)、试比较哪一种方案更好，说明理由．

查看试题解析
22. 已知函数 $f (x) = e^{x} - a x + x$ ．

(1)、讨论函数f(x)的单调性；

(2)、当x＞0时， $f (x) \geq x^{2} + 1$ 恒成立，求实数a的取值范围．

查看试题解析