广东省佛山市顺德区2020-2021学年高二下学期数学期末考试试卷
试卷更新日期:2021-08-31 类型:期末考试
一、单选题
-
1. 设复数 满足 ,则复数 的虚部为( )A、 B、 C、 D、2. 曲线 : 在点 处的切线方程为( )A、 B、 C、 D、3. 在端午小长假期间,某办公室要从4名职员中选出若干人在3天假期坚守岗位,每天只需1人值班,则不同的排班方法有( )A、12种 B、24种 C、64种 D、81种4. 已知函数 的图象如图所示,则其导函数的图象大致形状为( )
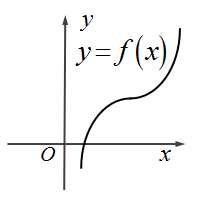 A、
A、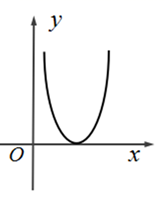 B、
B、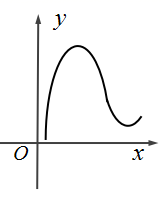 C、
C、 D、
D、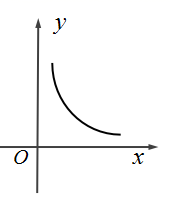 5. 在一次年级数学竞赛中,高二(20)班有10%的同学成绩优秀.已知高二(20)班人数占该年级的5%,而年级数学优秀率为2%.现从该年级任意选取一位同学,如果此人成绩优秀,则他来自高二(20)班的概率为( )A、10% B、15% C、20% D、25%6. 已知随机变量 , ,则 ( )A、 B、 C、 D、7. 某射手每次射击击中目标的概率固定,他准备进行 ( )次射击,设击中目标的次数记为 ,已知 且 ,则 ( )A、 B、 C、1 D、28. 已知函数 有三个零点,则实数 的取值范围是( )A、 B、 C、 D、
5. 在一次年级数学竞赛中,高二(20)班有10%的同学成绩优秀.已知高二(20)班人数占该年级的5%,而年级数学优秀率为2%.现从该年级任意选取一位同学,如果此人成绩优秀,则他来自高二(20)班的概率为( )A、10% B、15% C、20% D、25%6. 已知随机变量 , ,则 ( )A、 B、 C、 D、7. 某射手每次射击击中目标的概率固定,他准备进行 ( )次射击,设击中目标的次数记为 ,已知 且 ,则 ( )A、 B、 C、1 D、28. 已知函数 有三个零点,则实数 的取值范围是( )A、 B、 C、 D、二、多选题
-
9. 对于式子 ,下列说法正确的有( )A、它的展开式中第4项的系数等于135 B、它的展开式中第3项的二项式系数为20 C、它的展开式中所有项系数之和为64 D、它的展开式中第一项的系数为10. 在2021年2月25日召开的全国脱贫攻坚总结表彰大会上,我国庄严宣告:脱贫攻坚战取得了全面胜利,现行标准下农村贫困人口全部脱贫!下图表示的是中国农村每年减少贫困人口的数量,以下说法正确的是( )
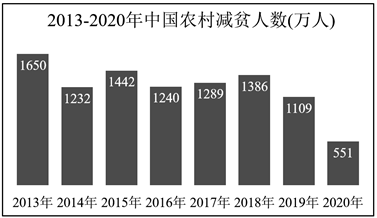 A、2014年与2016年农村贫困人口基本持平 B、2013-2020年农村贫困人口逐年减少 C、2013-2019年农村贫困人口平均每年减少了1300万以上 D、2012年底农村贫困人口还有9000万以上11. 2021年5月18日,《佛山市第七次全国人口普查公报》发布.公报显示,佛山市常住人口为9498863人.为了进一步分析数据特征,某数学兴趣小组先将近五次人口普查数据作出散点图(横坐标为人口普查的序号,第三次普查记为1,……,第七次普查记为5,纵坐标为当次人口普查佛山市人口数),再利用不同的函数模型作出回归分析,如下图,以下说法正确的是( )
A、2014年与2016年农村贫困人口基本持平 B、2013-2020年农村贫困人口逐年减少 C、2013-2019年农村贫困人口平均每年减少了1300万以上 D、2012年底农村贫困人口还有9000万以上11. 2021年5月18日,《佛山市第七次全国人口普查公报》发布.公报显示,佛山市常住人口为9498863人.为了进一步分析数据特征,某数学兴趣小组先将近五次人口普查数据作出散点图(横坐标为人口普查的序号,第三次普查记为1,……,第七次普查记为5,纵坐标为当次人口普查佛山市人口数),再利用不同的函数模型作出回归分析,如下图,以下说法正确的是( )
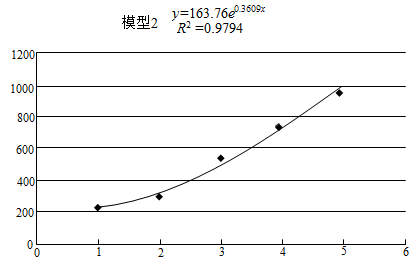 A、佛山市人口数与普查序号呈正相关关系 B、散点的分布呈现出很弱的线性相关特征 C、回归方程2的拟合效果更好 D、应用回归方程1可以预测第八次人口普查时佛山市人口会超过1400万12. 已知函数 ,则下列结论正确的是( )A、函数 存在极大值和极小值 B、函数 不存在最小值与最大值 C、当 时,函数 最大值为 D、当 时,函数 最小值为
A、佛山市人口数与普查序号呈正相关关系 B、散点的分布呈现出很弱的线性相关特征 C、回归方程2的拟合效果更好 D、应用回归方程1可以预测第八次人口普查时佛山市人口会超过1400万12. 已知函数 ,则下列结论正确的是( )A、函数 存在极大值和极小值 B、函数 不存在最小值与最大值 C、当 时,函数 最大值为 D、当 时,函数 最小值为三、填空题
-
13. 复数 、 在复平面内的对应点分别为 、 ,已知点 与 关于 轴对称,且 ,则14. 在6张奖券中有 张有奖、其余无奖,从中任取2张,至少有1张有奖的概率为 ,则 .15. 某田径队6位运动员的体测成绩如下:甲78,乙86,丙64,丁77,戊83,己93.现从中挑选3位运动员参加集体赛,挑选条件为:
①丁一定要参加;
②3人的体测成绩总分要超过240(不含240);
③3人的体测成绩方差要小.
那么参加集体赛3人名单应为 .
16. 已知函数 的导函数为 ,且函数 的图像经过 点,则函数 的表达式为 ;若对任意一个负数 ,不等式 恒成立,则整数 的最小值为 .四、解答题
-
17. 已知复数 ,( ),
(Ⅰ)若 在复平面内对应的点在虚轴的上半轴(不含原点),求复数 ;
(Ⅱ)若 ,求实数 的值.
18. 已知函数 , ,且图像过点 .(1)、求 的单调区间;(2)、当 时,求 的最大值 和最小值 .19. 《中国居民营养与慢性病状况报告(2020)年》报告显示,中国成人平均身高继续增长,居民超重、肥胖问题不断凸显.各年龄组居民超重率、肥胖率继续上升,18-44岁居民超重率和肥胖率分别为34%和16%.不健康的生活方式对超重、肥胖产生的影响是巨大的,超重、肥胖的控制必须坚持预防为主.(1)、根据以上数据,从18-44岁居民中任选2人,求肥胖人数的分布列;(2)、研究人员在某小区随机调查了男性居民45人,女性居民55人,其中男性超重人数有25人,女性超重人数为15人,请列出 列联表,并判断是否有99.5%的把握认为超重与性别有关.参考公式与数据: ,其中
P(K2≥k0)
0.150
0.100
0.050
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
20. 某工厂为了调查一批产品的质量情况,随机抽取了10件进行检测,质量指标 ( )分值如下:38,70,50,43,48,53,49,57,60, 并计算出样本质量指标平均数为53.7,标准差为9.9.生产合同中规定:质量指标在63分以上的产品为优质品,一批产品中优质品的占比不得低于15%.(1)、从这10件样品中任意抽取2件,求恰有1件优质品的概率;(2)、根据生产经验,可以认为这种产品的质量指标服从正态分布 ,其中 近似为样品平均数, 近似为样本方差,那么这批产品中优质品的占比是否满足生产合同的要求?请说明理由.附:若 ,则 , .
21. 某蛋糕厂商在两个社区分别开了连锁店A和B,通过一段时间的经营统计,店A和店B每日销售的蛋糕数 , 的分布列如下:3
4
5
6
2
4
6
(1)、求店A在3天共卖出15个蛋糕的概率;(2)、为了防止食品浪费,保障国家粮食安全,《中华人民共和国反食品浪费法》自2021年4月29日起施行.蛋糕保质期短,当日没销售出去只能作垃圾处理.该蛋糕厂商积极响应国家要求,决定今后每日仅生产10个蛋糕给两家连锁店,那么在市场需求不变的情况下如何分配这10个蛋糕最优?请说明理由.22. 已知函数 ( 为常数),函数 ,(Ⅰ)讨论函数 的单调性;
(Ⅱ)当 时,求证: ;
(Ⅲ)当 , 时,已知方程 有且只有两个不相等的实数根 , 且 ;方程 有且只有两个不相等的实数根 , 且 .求证: .