初中数学湘教版八年级上册2.3等腰三角形 同步练习

试卷更新日期：2021-08-31 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 已知等腰三角形的一个内角等于 50° ，则该三角形的一个底角是（    ）
    A、65° B、50° 或 60° C、65° 或 50° D、50°

    查看试题解析

  • 2. 若等腰三角形的周长是 22cm ，其中一边长为 10cm ，则腰长是（　　）
    A、10cm B、6cm C、6cm 或 10cm D、无法确定

    查看试题解析

  • 3. 等腰三角形的周长是 16cm，其中一边长为4cm，则该等腰三角形的底边长为（  ）
    A、8cm B、4cm C、10cm D、4cm或8cm

    查看试题解析

  • 4. 下列说法错误的是（　　）
    A、有两边相等的三角形是等腰三角形 B、直角三角形不可能是等腰三角形 C、有两个角为60°的三角形是等边三角形 D、有一个角为60°的等腰三角形是等边三角形

    查看试题解析

  • 5. 一个角是 60∘ 的等腰三角形是（   ）
    A、等腰直角三角形 B、等边三角形 C、直角三角形 D、上述都正确

    查看试题解析

  • 6. 下列各组数据能作为一个等腰三角形各边长的是（  ）
    A、2 ， 2 ， 4 B、2 ， 3 ， 4 C、4 ， 2 ， 4 D、3 ， 3 ， 7

    查看试题解析

  • 7. 在等腰三角形ABC中，它的两边长分别为8cm和4cm，则它的周长为（   ）
    A、10cm B、12 cm C、20 cm或16 cm D、20 cm

    查看试题解析

  • 8. 如图，已知AB＝AC，AD是△ABC的高，下列结论不一定正确的是（　　）

    A、∠B＝60° B、∠B＝∠C C、∠BAD＝∠CAD D、BD＝CD

    查看试题解析

  • 9. 如图：用一张长为4cm，宽3cm的长方形纸片，过两个顶点剪一个三角形，按裁剪线长度所标的数据（单位：cm）不可能实现的是（   ）
    A、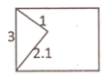 B、 C、 D、

    查看试题解析

  • 10. 如图，等边△ABC的边长是6，则高AD＝（  ）

    A、3 B、23 C、32 D、33

    查看试题解析

二、填空题

  • 11. 面积为48的等腰三角形底边上的高为6，则腰长为 ．

    查看试题解析

  • 12. 已知等边三角形的边长是2，则这个三角形的面积是 ． （保留准确值）

    查看试题解析

  • 13. 若等腰三角形一腰上的高等于腰长的一半，则此等腰三角形的二个底角的度数等于 度．

    查看试题解析

  • 14. 老师在投影屏上展示了如下一道试题：

    已知：如图，BD平分∠ABC，AB＝AD.求证：AD∥BC.

    证明：∵BD平分∠ABC，

    ∴∠ABD＝∠CBD（①角平分线定义）.

    ∵AB＝AD，

    ∴∠ABD＝∠ADB（②等角对等边）.

    ∴③∠ADB＝∠DBC，

    ∴AD∥BC（④内错角相等，两直线平行）.

    则以上证明过程中，结论或者依据错误的一项是.

    查看试题解析

  • 15. 如图，已知AB=AC，AD=BD=BC.在BC延长线上取点C1 ， 连接DC1 ， 使DC=CC1 ， 在CC1延长线上取点C2 ， 在DC1上取点E，使EC1=C1C2 ， 同理FC2=C2C3 ， 若继续如此下去直到C2021 ， 则∠C2021的度数为.

    查看试题解析

  • 16. 如图，AD是等边 △ ABC的中线，E是AC上一点，且AD=AE，则∠EDC=°

    查看试题解析

三、解答题

  • 17. 如图，△ABC是等边三角形，DF⊥AB，DE⊥CB，EF⊥AC，求证：△DEF是等边三角形．

    查看试题解析

  • 18. 如图，已知在△ABC中，△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O，MN过点O，且MN∥BC，分别交AB、AC于点M、N．求证：MN=CN﹣BM．

    查看试题解析

四、作图题

  • 19. 在如图的正方形网格中，每个小正方形的边长都是1，请在图中画出2个形状不同的等腰三角形，使它的腰长为 5 ，且顶点都在格点上，则满足条件的形状不同的等腰三角形共多少个．

    查看试题解析

  • 20. 已知△ABC的三条边长分别为2，5，6，在△ABC所在平面内画一条直线，将△ABC分成两个三角形，使其中一个三角形为等腰三角形.

    (1)、这样的直线最多可以画条；
    (2)、请在三个备用图中分别画出符合条件的一条直线，要求每个图中得到的等腰三角形腰长不同，尺规作图，不写作法，保留作图痕迹.

    查看试题解析

五、综合题

  • 21. 已知：如图，在△ADC中，AD＝CD ， 且AB∥DC ， CB⊥AB于B ， CE⊥AD交AD的延长线于E ， 连接BE ．

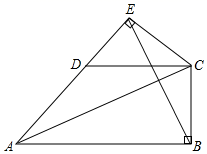    (1)、求证：CE＝CB；
    (2)、若∠CAE＝30°，CE＝2，求BE的长度．

    查看试题解析

  • 22. 在 ΔABC 中，AB=20cm，BC=16cm，点D为线段AB的中点，动点P以2cm/s的速度从B点出发在射线BC上运动，同时点Q以 a cm/s( a >0且 a≠2 ）的速度从C点出发在线段CA上运动，设运动时间为 x 秒。

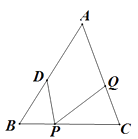    (1)、若AB=AC，P在线段BC上，求当 a 为何值时，能够使 ΔBPD 和 ΔCQP 全等？
    (2)、若 ∠B=60° ，求出发几秒后， ΔBDP 为直角三角形？
    (3)、若 ∠C=70° ，当 ∠CPQ 的度数为多少时， ΔCPQ 为等腰三角形？（请直接写出答案，不必写出过程）

    查看试题解析

  • 23. 如图

    (1)、问题发现：如图1，如果 △ABC 和 △ADE 均为等边三角形 ( 等边三角形的三条边都相等，三个角都是 60°) ，点B、E、D三点在同一直线上，连接 CD. 则CD与BE的数量关系为； ∠BDC 的度数为度．
    (2)、探究：如图2，若 △ABC 为三边互不相等的三角形，以它的边AB、AC为边分别向外作等边 △ABD 与等边 △ACE ，连接BE和CD相交于点O ， AB交CD于点F ， AC交BE于G ， 则CD与BE还相等吗？若相等，请证明，若不相等，说明理由：并请求出 ∠BOD 的度数？

    查看试题解析