广西壮族自治区柳州市柳江区2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2021-08-31 类型:期中考试
一、单选题
-
1. 下列长度的3根小木棒不能搭成三角形的是( )A、2cm,3cm,4cm B、1cm,2cm,3cm C、3cm,4cm,5cm D、4cm,5cm,6cm2. 下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知一个正多边形的内角是140°,则这个正多边形的边数是( )A、6 B、7 C、8 D、94. 如图,在△ABC中,BC边上的高为( )
3. 已知一个正多边形的内角是140°,则这个正多边形的边数是( )A、6 B、7 C、8 D、94. 如图,在△ABC中,BC边上的高为( )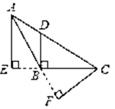 A、BD B、CF C、AE D、BF5. 平面直角坐标系内的点A(-1,2)与点B(-1,-2)关于( )A、y轴对称 B、x轴对称 C、原点对称 D、直线y=x对称6. 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,若添加下列一个条件后,仍然不能证明△ABC≌△DEF,则这个条件是( )
A、BD B、CF C、AE D、BF5. 平面直角坐标系内的点A(-1,2)与点B(-1,-2)关于( )A、y轴对称 B、x轴对称 C、原点对称 D、直线y=x对称6. 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,若添加下列一个条件后,仍然不能证明△ABC≌△DEF,则这个条件是( ) A、∠A=∠D B、BC=EF C、∠ACB=∠F D、AC=DF7. 如图,在 Rt△ABC中,∠C=90°,AC=3,BC=4,AB的垂直平分线交BC于点D,连接AD,则△ACD的周长是( )
A、∠A=∠D B、BC=EF C、∠ACB=∠F D、AC=DF7. 如图,在 Rt△ABC中,∠C=90°,AC=3,BC=4,AB的垂直平分线交BC于点D,连接AD,则△ACD的周长是( ) A、7 B、8 C、9 D、108. 已知等腰三角形的两边长分别为3和6,则它的周长等于( )
A、7 B、8 C、9 D、108. 已知等腰三角形的两边长分别为3和6,则它的周长等于( )
A、12 B、12或15 C、15 D、15或189. 通过如下尺规作图,能确定点D是BC边中点的是( )A、 B、
B、 C、
C、 D、
D、 10. 如图所示,△ABP与△CDP是两个全等的等边三角形,且PA⊥PD , 有下列四个结论:①∠PBC=15°,②AD∥BC , ③PC⊥AB , ④四边形ABCD是轴对称图形,其中正确的个数为( )
10. 如图所示,△ABP与△CDP是两个全等的等边三角形,且PA⊥PD , 有下列四个结论:①∠PBC=15°,②AD∥BC , ③PC⊥AB , ④四边形ABCD是轴对称图形,其中正确的个数为( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,已知图中的两个三角形全等,则∠α度数是°.
 12. 如图,∠1=∠2,要使△ABD≌△ACD,需添加的一个条件是 (只添一个条件即可).
12. 如图,∠1=∠2,要使△ABD≌△ACD,需添加的一个条件是 (只添一个条件即可).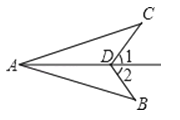 13. 如图, 、 是 的角平分线, , 、 相交于 ,则 的度数是.
13. 如图, 、 是 的角平分线, , 、 相交于 ,则 的度数是. 14. 已知点 , 关于x轴对称,则 .15. 等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为 .16.
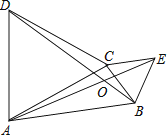
14. 已知点 , 关于x轴对称,则 .15. 等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为 .16.如图,在△ABC中,分别以AC、BC为边作等边三角形ACD和等边三角形BCE,连接AE、BD交于点O,则∠AOB的度数为 .
三、解答题
-
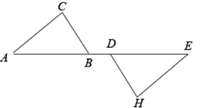
17. 已知:如图,点B,D在线段AE上,AD=BE,AC∥EH,∠C=∠H.求证:BC=DH.
 18. 请在下列三个2×2的方格中,各画出一个三角形,要求所画三角形是图中三角形经过轴对称变换后得到的图形,且所画的三角形顶点与方格中的小正方形顶点重合,并将所画三角形涂上阴影.(注:所画的三个图形不能重复)
18. 请在下列三个2×2的方格中,各画出一个三角形,要求所画三角形是图中三角形经过轴对称变换后得到的图形,且所画的三角形顶点与方格中的小正方形顶点重合,并将所画三角形涂上阴影.(注:所画的三个图形不能重复) 19. 请将下列证明过程补充完整.
19. 请将下列证明过程补充完整.求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知:如图, 是 的外角, 平分 .
求证: .
证明:∵ ,∴ ( ),
( ),
∵ 平分 ,
∴ ( ),
∴ _▲_( ),
∴ ( ).
 20. 如图,在平面直角坐标系中, .
20. 如图,在平面直角坐标系中, . (1)、作出 关于 轴的对称图形 ;(2)、写出点 的坐标.(3)、在 轴上找一点 ,使 的长最短.21. 如图,在△ABC中,∠B=50°,∠C=70°,AD是高,AE是角平分线,求∠EAD的度数.
(1)、作出 关于 轴的对称图形 ;(2)、写出点 的坐标.(3)、在 轴上找一点 ,使 的长最短.21. 如图,在△ABC中,∠B=50°,∠C=70°,AD是高,AE是角平分线,求∠EAD的度数.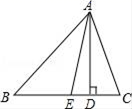 22. 如图,在△ABC中,AB的垂直平分线MN交AB于点D,交AC于点E,且AC=15cm,△BCE的周长等于25cm.
22. 如图,在△ABC中,AB的垂直平分线MN交AB于点D,交AC于点E,且AC=15cm,△BCE的周长等于25cm.
(1)、求BC的长;(2)、若∠A=36°,并且AB=AC.求证:BC=BE.23. 如图 (1)、某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在 中, , ,直线 经过点A , BD⊥直线l , CE⊥直线l , 垂足分别为点D、E.证明:DE=BD+CE.(2)、组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在 中,AB=AC , D、A、E三点都在直线l上,并且有 ,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过 的边AB、AC向外作正方形ABDE和正方形ACFG , AH是BC边上的高,延长HA交EG于点1 , 求证:I是EG的中点.
(1)、某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在 中, , ,直线 经过点A , BD⊥直线l , CE⊥直线l , 垂足分别为点D、E.证明:DE=BD+CE.(2)、组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在 中,AB=AC , D、A、E三点都在直线l上,并且有 ,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过 的边AB、AC向外作正方形ABDE和正方形ACFG , AH是BC边上的高,延长HA交EG于点1 , 求证:I是EG的中点.