广西壮族自治区防城港市防城区2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期：2021-08-31 类型：期中考试
一、单选题
-
1. 用下列长度的三根铁条首尾顺次联结，不能做成三角形框架的是（ ）A、3cm 10cm 8cm B、3cm 8cm 8cm C、3cm 3cm 8cm D、10cm 10cm 8cm2. 一个正多边形的内角和为540°，则这个正多边形的每一个内角是（ ）A、120° B、108° C、90° D、60°3. 将一副三角尺按如图所示的方式摆放，则 的大小为（ ）
A、 B、 C、 D、4. 如图，△ABC≌△DEF，已知BC＝5cm，BF＝7cm，则EC长为（ ）
A、1cm B、2cm C、3cm D、4cm5. 如图，在△ABC中，BE、CE分别是∠ABC和∠ACB的平分线，过点E作DF∥BC交AB于D，交AC于F，若AB=4，AC=3，则△ADF周长为（ ）
A、6 B、7 C、8 D、106. 如图，将两根钢条AA′、BB′的中点 O连在一起，使AA′、BB′能绕着点O自由转动，就做成了一个测量工具，由三角形全等可知A′B′的长等于内槽宽AB，那么判定△OAB≌△OA′B′的理由是（ ）
A、SAS B、ASA C、SSS D、AAS7. 若从一多边形的一个顶点出发，最多可引10条对角线，则它是（ ）A、十三边形 B、十二边形 C、十一边形 D、十边形8. 等腰三角形的周长为13 cm，其中一边长为3 cm，则该等腰三角形的底边长为（ ）A、3cm B、5cm C、7cm或3cm D、8cm9. 如图，已知∠AOB，以点O为圆心，任意长为半径画弧，交OA于点C，交OB于点D，再分别以C，D为圆心，以大于 CD长为半径画弧，两弧交于点F，作射线OF，点P为OF上一点，PE⊥OB，垂足为点E，若PE＝5，则点P到OA的距离为（ ）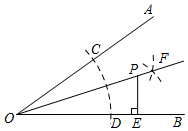
A、5 B、4 C、3 D、10. 如图，在 中，DE是AC的垂直平分线，且分别交BC，AC于D、E两点， ， ，则 的度数为（ ）
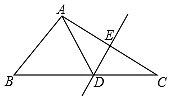A、 B、 C、 D、11. 如图，在△ABC中，AB=20cm，AC=12cm，点P从点B出发以每秒3cm速度向点A运动，点Q从点A同时出发以每秒2cm速度向点C运动，其中一个动点到达端点，另一个动点也随之停止，当△APQ是以PQ为底的等腰三角形时，运动的时间是（ ）秒
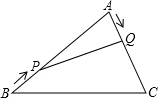A、2.5 B、3 C、3.5 D、412. 如图，△ABC中，∠ABC＝45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，DH⊥BC于H，交BE于G，下列结论：①BD＝CD；②AD+CF＝BD；③CE＝ BF；④AE＝BG.其中正确的是（ ）
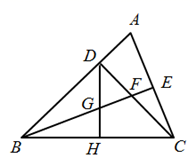A、①② B、①③ C、①②③ D、①②③④二、填空题
-
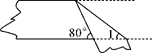
13. 已知点A（x，2），B（﹣3，y），若A，B关于x轴对称，则x+y等于 ．14. 三角形的三边长分别为3、7、a，且a为偶数，则这个三角形的周长为 ．15. 如图，一个宽度相等的纸条，如图折叠，则∠1的度数是.
16. 如图，AB=AC，要使△ABE≌△ACD，应添加的条件是（添加一个条件即可）．
17. 如图，在△ABC中，∠ABC=50°，∠ACB=80°，BP平分∠ABC，CP平分∠ACB，则∠BPC的大小是度．
18. 如图，在△ABC中，已知点D、E、F分别为BC、AD、BE的中点，且S△ABC=8cm2 ， 则图中阴影部分△CEF的面积是.
三、解答题
-
19. 一个多边形，它的内角和比外角和的4倍多180°，求这个多边形的边数及内角和度数．
20. 如图，AD、AF分别是△ABC中∠BAC的平分线和BC边上的高，已知∠B＝36°，∠C＝76°，求∠DAF的大小.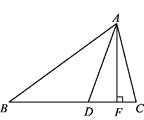
21. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形ABC（顶点是网格线的交点的三角形）的顶点B、C的坐标分别为（﹣2，0），（﹣1，2）.
（ 1 ）请在如图所示的网格中根据上述点的坐标建立对应的直角坐标系；（只要画图，不需要说明）
（ 2 ）在（1）中建立的平面直角坐标系中，先画出△ABC关于y轴对称的图形△A1B1C1 ， 再画出△A1B1C1关于x轴对称的图形△A2B2C2.
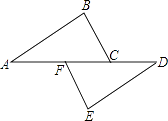
22. 如图，△ABC与△DCB中，AC与BD交于点E，且∠A=∠D，AB=DC．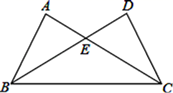
(1)、求证：△ABE≌△DCE；(2)、当∠AEB=60°，求∠EBC的度数．23. 如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB=DE，∠A=∠D，AF=DC．求证：BC∥EF．
