广西玉林市陆川县2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2021-08-31 类型：期中考试

进入出卷网下载

一、单选题

1. 如图，张叔叔家的凳子坏了，于是他给凳子加了两根木条，这样凳子就比较牢固了，他所应用的数学原理是（）

A、三角形的稳定性 B、两点之间线段最短 C、垂线段最短 D、对顶角相等

查看试题解析
2. 如图，在△ABC中，MN $//$ AC，BD⊥AC于点D，交MN于点 E，则下列说法中，不正确的是（）

A、BD是△ABC的高 B、ME是△ABD的高 C、BE是△BMN的高 D、CD是△BCD的高

查看试题解析
3. 长为9，6，5，4的四根木条，选其中三根组成三角形，选法有（）

A、1种 B、2种 C、3种 D、4种

查看试题解析
4. 如图，乐乐书上的三角形墨迹污染了一部分，很快他就画出一个三角形与书上的三角形全等，这两个三角形全等的依据是（）

A、 $S S S$ B、 $A S A$ C、 $A A S$ D、 $S A S$

查看试题解析
5. 将一副直角三角板，按如图所示叠放在一起，则图中∠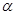 的度数是（）

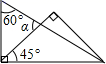A、45^o B、60^o C、75^o D、90^o

查看试题解析
6. 点P在∠MON的平分线上，点P到OM边的距离等于4，点Q是ON边上任意一点，下列关于线段PQ长度的描述正确的是（）

A、PQ<4 B、PQ≤4 C、PQ>4 D、PQ≥4

查看试题解析
7. 若 ${(2 m - 1)}^{0} = 1$ ，则 $m$ 的值为（）

A、0 B、 $\neq 0$ C、 $\frac{1}{2}$ D、 $\neq \frac{1}{2}$

查看试题解析
8. 要使 $(6 x - m) (3 x + 1)$ 的结果不含 $x$ 的一次项，则 $m$ 的值等于（）

A、2 B、3 C、0 D、1

查看试题解析
9. 下列说法：
①全等三角形的对应边相等、对应角相等；②全等三角形的周长相等；③面积相等的两个三角形全等；④全等三角形：对应边上的高相等，对应边上中线相等，对应角平分线相等.其中正确的说法为（）

A、②③④ B、①②③ C、①②④ D、①②③④

查看试题解析
10. 若 $x^{2} + 6 x + p = {(x - q)}^{2}$ 则 $p$ ， $q$ 的值分别为（）

A、6，6 B、9，-3 C、3，-3 D、9，3

查看试题解析
11. 若 $2^{2 m + 1} + 4^{m} = 48$ ，则 $m$ 的值是（）

A、4 B、3 C、2 D、8

查看试题解析
12. 如图，四边形纸片ABCD中，∠A=65°，∠B=85°，将纸片折叠，使C，D落在AB边上的 $C^{'}$ ， $D^{'}$ 处，折痕为MN，则 $∠ A M D^{'} + ∠ B N C^{'} =$ （）

A、60° B、70° C、80° D、85°

查看试题解析

二、填空题

13. 若n边形的每一个外角都是72°，则边数n为.

查看试题解析
14. 一个等腰三角形的两边长分别为4.6cm和9.2cm，则这个三角形的周长为cm.

查看试题解析
15. 如图，已知△ABC的周长是21，OB ， OC分别平分∠ABC和∠ACB ， OD⊥BC于D ，且OD＝4，△ABC的面积是．

查看试题解析
16. 若 $a^{m} = 5$ ， $a^{n} = 8$ ，则 $a^{m + n} =$ .

查看试题解析
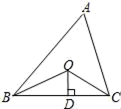17. 观察下列各式：1×3＝1²＋2×1；2×4＝2²＋2×2；3×5＝3²＋2×3；…….请你将猜想到的规律用正整数n表示出来：.

查看试题解析
18. 已知点A，B的坐标分别为（2，2），（2，4），O是原点，以A，B，P为顶点的三角形与 $△ A B O$ 全等，写出所有符合条件的点P的坐标：.

查看试题解析

三、解答题

19. 因式分解

(1)、 $9 a^{3} - a b^{2}$

(2)、 $16 m^{2} - n^{2} - 6 n - 9$

查看试题解析
20. 计算/化简求值

(1)、计算： $(\frac{1}{4} a^{3} b^{2} c - \frac{1}{6} a^{2} b^{2} c^{2}) \div (- \frac{1}{2} a^{2} b^{2} c)$

(2)、先化简，再求值： ${(m + 2 n)}^{2} + (m + n) (- m + n)$ ，其中 $m = - 1$ ， $n = 2$

查看试题解析
21. 如图，在 $△ A B C$ 中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别为点E， F，∠B=∠C.求证：DE=DF.

查看试题解析
22. 一个多边形的外角和等于内角和的 $\frac{2}{7}$ ，求这个多边形的边数．

查看试题解析
23. 已知：如图，线段 AB 和射线 BM 交于点 B.利用尺、规.完成以下作图，并保留作图痕迹.（不要求写作法）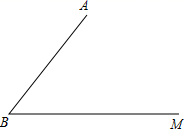

（ 1 ）在射线 BM 上求作一点 C，使AC＝AB；

（ 2 ）在线段 AB 上求作一点 D，使点D到BC，AC的距离相等；

查看试题解析
24. 已知在 $△ A B C$ 中，三边长分别为a，b，c，且满足等式 $a^{2} + b c - a c - b^{2} = 0 ，$ 请判断 $△ A B C$ 的形状，并写出你的理由.

查看试题解析
25. 如图，AD是 $△ A B C$ 的角平分线，且AB>AC，E为AD上任意一点，
求证： $A B - A C > E B - E C$ .

查看试题解析
26. 如图1，在△ABC中，AE⊥BC于，AE=BE，D是AE上的一点，且DE=CE，连接BD、AC．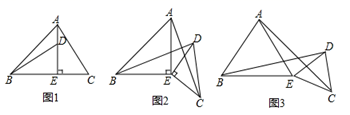

(1)、试判断BD与AC的位置关系和数量关系，并说明理由；

(2)、如图2，若将△DCE绕点E旋转一定的角度后，仍然有DE⊥EC，DE=CE，试判断BD与AC的位置关系和数量关系是否发生变化，并说明理由；

(3)、如图3，若将(2)中的等腰直角三角形都换成等边三角形，其他条件不变：
①试猜想BD与AC的数量关系，并说明理由；

②你能求出BD与AC所成的角的度数吗？如果能，请直接写出该角的度数；如果不能，请说明理由．

查看试题解析