浙江省金华市金东区2021年数学中考适应性试卷
试卷更新日期:2021-08-31 类型:中考模拟
一、单选题
-
1. 等于( )A、2 B、-2 C、±2 D、2. 世界文化遗产长城总长约为6700000m,若将6700000用科学记数法表示为6.7×10n(n是正整数),则n的值为A、5 B、6 C、7 D、83. 已知一元二次方程 有一个根为2,则另一根为( )A、2 B、3 C、4 D、84. 若正比例函数y=kx的图象经过点(1,2),则k的值为( )A、 B、-2 C、 D、25. 抛物线 的顶点坐标是( )A、(3,1) B、(3,﹣1) C、(﹣3,1) D、(﹣3,﹣1)6. 一组数据:0,1,2,3,3,5,5,10的中位数是( )A、2.5 B、3 C、3.5 D、57. 如图,点E是▱ABCD的边CD的中点,AD,BE的延长线相交于点F,DF=3,DE=2,则▱ABCD的周长为( )
 A、5 B、7 C、10 D、148. 已知x﹣ =3,则4﹣ x2+ x的值为( )A、1 B、 C、 D、9. 如图,反比例函数y= (x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B'在此反比例函数的图象上,则t的值是( )
A、5 B、7 C、10 D、148. 已知x﹣ =3,则4﹣ x2+ x的值为( )A、1 B、 C、 D、9. 如图,反比例函数y= (x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B'在此反比例函数的图象上,则t的值是( ) A、 B、 C、 D、10. 已知二次函数y=﹣x2+x+c(c<0),当自变量为x1时,其函数值y1大于零;当自变量为x1﹣1与x1+1时,其函数值分别为y2 , y3 , 则( )A、y2>0,y3>0 B、y2>0,y3<0 C、y2<0,y3<0 D、y2<0,y3>0
A、 B、 C、 D、10. 已知二次函数y=﹣x2+x+c(c<0),当自变量为x1时,其函数值y1大于零;当自变量为x1﹣1与x1+1时,其函数值分别为y2 , y3 , 则( )A、y2>0,y3>0 B、y2>0,y3<0 C、y2<0,y3<0 D、y2<0,y3>0二、填空题
-
11. 分解因式: = .12. 有三张大小、形状及背面完全相同的卡片,卡片正面分别画有正三角形、正方形、圆,从这三张卡片中任意抽取一张,卡片正面的图形既是轴对称图形又是中心对称图形的概率是.13. 不等式组 的解集为.14.
已知△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD=1,连接DE,则DE= .
 15. 如图,动点P从(0,3)出发,沿所示的方向运动,每当碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当点P第2021次碰到矩形的边时,点P的坐标为.
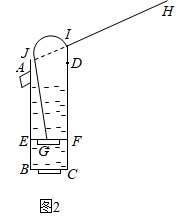
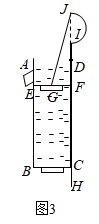
15. 如图,动点P从(0,3)出发,沿所示的方向运动,每当碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当点P第2021次碰到矩形的边时,点P的坐标为.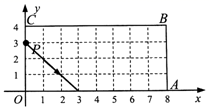 16. 已知,有一个井泵如图1所示,它的一个纵向截面如图2,当活塞EF向上移动时,底面BC上的阀门打开,EF上的阀门关闭,外部液体被吸入活塞下方的空间内,活塞EF上方的液体被上推;当活塞EF向下移动时,BC上的阀门关闭,EF上的阀门打开,液体从活塞EF下方空间被压入活塞内EF上方空间.在图2中,点J在直径AD上,水泵底面直径BC=10cm,活塞直径EF∥BC,G为EF中点.手柄IH支撑杆ID长2 cm,弧JI是直径为4 cm的半圆,连轴JG的长为25cm,(点C,D,F,I四点共线,J,I,H三点共线,水泵材质厚度忽略不计),则DF=cm,当手柄IH从图2位置按压到与CD重合(如图3)过程中井泵的最大出水量是cm3.
16. 已知,有一个井泵如图1所示,它的一个纵向截面如图2,当活塞EF向上移动时,底面BC上的阀门打开,EF上的阀门关闭,外部液体被吸入活塞下方的空间内,活塞EF上方的液体被上推;当活塞EF向下移动时,BC上的阀门关闭,EF上的阀门打开,液体从活塞EF下方空间被压入活塞内EF上方空间.在图2中,点J在直径AD上,水泵底面直径BC=10cm,活塞直径EF∥BC,G为EF中点.手柄IH支撑杆ID长2 cm,弧JI是直径为4 cm的半圆,连轴JG的长为25cm,(点C,D,F,I四点共线,J,I,H三点共线,水泵材质厚度忽略不计),则DF=cm,当手柄IH从图2位置按压到与CD重合(如图3)过程中井泵的最大出水量是cm3.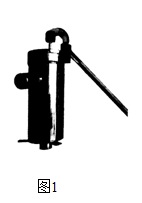
三、解答题
-
17. 计算: .18. 解分式方程: = .19. 如图,已知一次函数y1=kx+b与反比例函数y2= 的图象交于 、 两点.分别求出y1和y2的解析式.
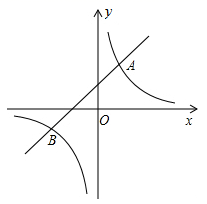 20. 为了解学校九年级学生体育成绩,安排了体育中考模拟测试,现从中随机抽取部分学生的体育成绩进行分组(A:40分; B:39﹣36分; C:35﹣32分; D:31﹣24分; E:23﹣0分)统计如下:
20. 为了解学校九年级学生体育成绩,安排了体育中考模拟测试,现从中随机抽取部分学生的体育成绩进行分组(A:40分; B:39﹣36分; C:35﹣32分; D:31﹣24分; E:23﹣0分)统计如下: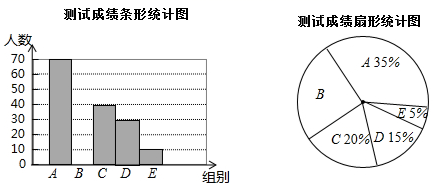
根据上面提供的信息,回答下列问题:
(1)、这次调查中,抽取的学生人数为多少?并将条形统计图补充完整.(2)、如果把成绩在24分以上(含24分)定为合格,估计该校今年800名九年级学生中,体育模拟测试成绩为合格的学生人数有多少人?21. 如图,在△ABC中,AB=AC,D,E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD'E,连接D'C,若BD=CD'. (1)、求证:△ABD≌△ACD'.(2)、若∠BAC=100°,求∠DAE的度数.22. 如图,四边形ABCD的四个顶点在以AC为直径的⊙O上,点D为 的中点,过圆心O作OE⊥AB于点E,交BD于点F,AC=10,OF=1.
(1)、求证:△ABD≌△ACD'.(2)、若∠BAC=100°,求∠DAE的度数.22. 如图,四边形ABCD的四个顶点在以AC为直径的⊙O上,点D为 的中点,过圆心O作OE⊥AB于点E,交BD于点F,AC=10,OF=1.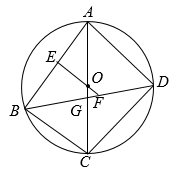 (1)、求证:∠ABD=45°.(2)、求AB的长.(3)、求FG的长.23. 已知在平面直角坐标系xOy中,x轴上有一个动点M,记点M横坐标为m,抛物线y=2x2+m和直线y=mx+2交于点A,B(点B在点A右侧),记抛物线y=2x2+m的顶点为P.(1)、当m=1时,求△ABP的面积.(2)、当点M从点(﹣1,0)运动到(1,0)的过程中,求线段PB所扫过的区域面积.(3)、当∠PBA=90°时,求m的值.24. 在菱形ABCD中,AB=4,∠A=120°,点E是AB的中点,点F在边BC上,连接DE,EF.
(1)、求证:∠ABD=45°.(2)、求AB的长.(3)、求FG的长.23. 已知在平面直角坐标系xOy中,x轴上有一个动点M,记点M横坐标为m,抛物线y=2x2+m和直线y=mx+2交于点A,B(点B在点A右侧),记抛物线y=2x2+m的顶点为P.(1)、当m=1时,求△ABP的面积.(2)、当点M从点(﹣1,0)运动到(1,0)的过程中,求线段PB所扫过的区域面积.(3)、当∠PBA=90°时,求m的值.24. 在菱形ABCD中,AB=4,∠A=120°,点E是AB的中点,点F在边BC上,连接DE,EF. (1)、取AD中点G,连接EF,EG.DE与FG交于点H.
(1)、取AD中点G,连接EF,EG.DE与FG交于点H.①如图1,当点F与点B重合时,求证:△EGH∽△DBH.
②如图2,当∠EDF=2∠GED时,求线段EF的长.
(2)、连接AF,如图3,当∠DEF=∠BAF时,求BF的长.