浙江省嘉兴市南湖区2021年数学中考二模试卷

试卷更新日期：2021-08-31 类型：中考模拟

进入出卷网下载

一、单选题

1. 在-5、-1、0、3这四个有理数中，最小的有理数是（）

A、-5 B、-1 C、0 D、3

查看试题解析
2. 下列计算中，结果正确的是（）

A、 $a^{2} + a^{2} = a^{4}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 ${(a^{3})}^{2} = a^{5}$ D、 $a^{3} \div a^{2} = a$

查看试题解析
3. 为庆祝中国共产党百年华诞，嘉兴启动了“百年百项”重大项目工程，计划总投资超2000亿元.数2000亿用科学记数法表示为（）

A、 $20 \times 10^{10}$ B、 $2 \times 10^{11}$ C、 $2 \times 10^{12}$ D、 $2 \times 10^{10}$

查看试题解析
4. 如图是一段水管的实物图，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 不等式 $4 - x \geq 2$ 的解在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 若数组3，3， $x$ ，4，5的平均数为4，则这组数中的（）

A、 $x = 4$ B、中位数为4 C、众数为3 D、中位数为 $x$

查看试题解析
7. 如图，在直角坐标系中， $△ A B C$ 的顶点 $B$ 的坐标为 $(- 1 ， 1)$ ，现以坐标原点 $O$ 为位似中心，作与 $△ A B C$ 的位似比为 $\frac{2}{3}$ 的位似图形 $△ A^{'} B^{'} C^{'}$ ，则 $B^{'}$ 的坐标为（）

A、 $(- \frac{2}{3} ， \frac{2}{3})$ B、 $(\frac{2}{3} ， - \frac{2}{3})$ C、 $(- \frac{2}{3} ， \frac{2}{3})$ 或 $(\frac{2}{3} ， - \frac{2}{3})$ D、 $(- \frac{2}{3} ， \frac{2}{3})$ 或 $(- \frac{2}{3} ， - \frac{2}{3})$

查看试题解析
8. 量角器圆心为 $O$ ，直径 $A B = 12$ ，一把宽为3的直尺的一边过 $O$ 点且与量角器交于 $C$ 、 $D$ 两点，如图所示，则弧 $C D$ 的长为（）

A、 $2 π$ B、 $\frac{3}{2} π$ C、 $\frac{1}{2} π$ D、 $π$

查看试题解析
9. 如图，矩形纸片 $A B C D$ 中， $A D = 6$ ， $E$ 是 $C D$ 上一点，连结 $A E$ ， $△ A D E$ 沿直线 $A E$ 翻折后点 $D$ 落到点 $F$ ，过点 $F$ 作 $F G ⊥ A D$ ，垂足为 $G$ .若 $A D = 3 G D$ ，则 $D E$ 的值为（）

A、 $\sqrt{5}$ B、 $\frac{5}{2}$ C、 $\frac{6 \sqrt{5}}{5}$ D、 $\frac{5 \sqrt{3}}{3}$

查看试题解析
10. 在平面直角坐标系中，已知点 $A (- 2 ， 2)$ ， $B (2 ， 1)$ ，若抛物线 $y = a x^{2} - 2 x + 1 (a \neq 0)$ 与线段 $A B$ 有两个不同的交点，则 $a$ 的取值范围是（）

A、 $- \frac{49}{32} < a \leq - \frac{3}{4}$ 或 $a \geq 1$ B、 $a \geq - \frac{3}{4}$ 或 $a < - \frac{49}{32}$ C、 $- \frac{3}{4} \leq a \leq 1$ 且 $a \neq 0$ D、 $a \leq - \frac{3}{4}$ 或 $a \geq 1$

查看试题解析

二、填空题

11. 分解因式： $a^{2} - 1$ =.

查看试题解析
12. 不透明袋子中装有除颜色外都相同的8个小球，其中白球5个，黑球3个.从中任意摸出一球恰为白球的概率为.

查看试题解析
13. 计算： $\frac{x^{2}}{x - 2} + \frac{4}{2 - x} =$ .

查看试题解析
14. “鸡兔同笼”是我国古代数学名著《孙子算经》上的一道题：今有鸡兔同笼，上有四十三头，下有一百零二足，问鸡兔各几何？若设笼中有鸡 $x$ 只，兔 $y$ 只，则可列出的二元一次方程组为.

查看试题解析
15. 如图所示，在 $10 \times 10$ 的正方形网格中有一半径为5的圆，一条折线将它分成甲、乙两部分. $S_{甲}$ 表示甲的面积，则 $S_{甲} =$ .

查看试题解析
16. 已知，如图， $△ A B C$ 中， $∠ B = 30 °$ ， $B C = 6$ ， $A B = 7$ ， $D$ 是 $B C$ 上一点， $B D = 4$ ， $E$ 为 $B A$ 边上一动点，以 $D E$ 为边向右侧作等边三角形 $△ D E F$ .

(1)、当 $F$ 在 $A B$ 上时， $B F$ 长为；

(2)、连结 $C F$ ，则 $C F$ 的取值范围为.

查看试题解析

三、解答题

17. 计算：

(1)、 $| 1 - \sqrt{3} | + {(\sqrt{2} - 1)}^{0}$

(2)、 ${(a - b)}^{2} + a b$

查看试题解析
18. 解方程组： ${\begin{matrix} 3 x - 2 y = 6 ① \\ x + y = 5 ② \end{matrix}$ ，小海同学的解题过程如下：
解：由②得 $y = 5 + x$ ，③ $\dots \dots \dots \dots \dots (1)$

把③代入①得 $3 x - 2 x + 5 = 6$ ， $\dots \dots \dots \dots \dots (2)$

$x = - 1 \dots \dots \dots \dots \dots (3)$

把 $x = - 1$ 代入③得 $y = 1$ ， $\dots \dots \dots \dots \dots (4)$

∴此方程组的解为 ${\begin{matrix} x = - 1 \\ y = 1 \end{matrix}$ . $\dots \dots \dots \dots \dots (5)$

判断小海同学的解题过程是否正确，若不正确，请指出错误的步骤序号，并给出正确的解题过程.

查看试题解析

19. 为了解我市九年级学生视力状况，抽取若干名学生进行视力检测，结果如下：

视力等级	$A$ （大于等于 $5.0$ ）	$B (4.9)$	$C (4.6 - 4.8)$	$D$ （小于等于 $4.5$ ）
人数	$a$	50	$c$	$d$

根据调查结果的统计数据，绘制成如图所示的一幅不完整的统计图，由图表中给出的信息解答下列问题：

各等级人数扇形统计图：

(1)、求本次抽查的学生人数；

(2)、按标准5.0及以上为正常，低于5.0都属于视力不佳.若该市共有45000名九年级学生，试估计视力不佳的学生人数.

查看试题解析

20. 已知， $∠ A B C$ 和 $∠ D E F$ 中， $A B // D E$ ， $B C // E F$ .试探究：

(1)、如图1， $∠ B$ 与 $∠ E$ 的关系是；

(2)、如图2，写出 $∠ B$ 与 $∠ E$ 的关系，并说明理由；

(3)、根据上述探究，请归纳得到一个真命题.

查看试题解析
21. 如图， $A B$ 是⊙O的直径， $E$ 是⊙O上一点， $A C$ 平分 $∠ B A E$ ，过点 $C$ 作 $C D ⊥ A E$ 交 $A E$ 延长线于点 $D$ .

(1)、求证： $C D$ 是⊙O的切线；

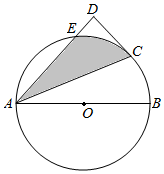(2)、若 $A B = 6$ ， $∠ B A C = 30 °$ ，求阴影部分的面积.

查看试题解析
22. 海绵拖把一般由长杆、U型挤压器、海绵及连杆（含拉杆）装置组成（如实物图），拉动拉杆可带动海绵进入挤压器的两压杆间，起到挤水的作用.（图1），（图2），（图3）是其挤水原理示意图， $A$ 、 $B$ 是拖把上的两个固定点，拉杆 $A P$ 一端固定在点 $A$ ，点 $P$ 与点 $B$ 重合，如（图1），拉动点 $P$ 可使拉杆绕着点 $A$ 转动，此时点 $C$ 沿着 $A B$ 所在直线上下移动，如（图2）.已知 $A B = 10 cm$ ，连杆 $P C$ 为 $40 cm$ ， $F G = 4 cm$ ， $M N = 8 cm$ .当 $P$ 点转动到射线 $B A$ 上时，如（图3）， $F G$ 落在 $M N$ 上，此时点 $D$ 与点 $E$ 重合，点 $I$ 与点 $H$ 重合.

(1)、求 $M E$ 的长；

(2)、转动 $A P$ ，当 $∠ P A C = 53 °$ 时，
①求点 $C$ 的上升高度；

②求点 $D$ 与点 $I$ 之间的距离（结果精确到 $0.1$ ）.（ $\sin 53 ° \approx \frac{4}{5}$ ， $\cos 53 ° \approx \frac{3}{5}$ ， $\sqrt{6} \approx 2.45$ ， $\sqrt{101} \approx 10.05$ ）

查看试题解析

23. 某公司销售一种成本为30元的工艺品.设该公司第

x

天销售这种工艺品的数量为

p

件，经统计发现第

1 \sim 20

天

p

与

x

之间的的函数关系式如下表，第21天开始

p

与

x

之间满足

p = - x + 92 (20 < x \leq 60)

的函数关系：

天数 $x$	1	2	3	4	5	…	20
件数 $p$	110	108	106	104	102	…	72

(1)、请观察表格，用所学过的函数知识求出第

1 \sim 20

天

p

与

x

的函数关系式；

(2)、若第

x

天每件工艺品的销售价格为

y

（元/件），

y

与

x

之间的关系满足如下关系：

y = {\begin{array}{l} x + 50 (1 \leq x \leq 30) \\ 75 (31 \leq x \leq 60) \end{array}

，问在这60天内，第几天的销售利润最大？最大利润是多少？

查看试题解析

24. 定义：平面直角坐标系 $x O y$ 中，过二次函数图象与坐标轴交点的圆，称为该二次函数的坐标圆.

(1)、已知点 $P (2 ， 2)$ ，以 $P$ 为圆心， $\sqrt{5}$ 为半径作圆.请判断⊙ $P$ 是不是二次函数 $y = x^{2} - 4 x + 3$ 的坐标圆，并说明理由；

(2)、已知二次函数 $y = x^{2} - 4 x + 4$ 图象的顶点为 $A$ ，坐标圆的圆心为 $P$ ，如图1，求 $△ P O A$ 周长的最小值；

(3)、已知二次函数 $y = a x^{2} - 4 x + 4 (0 < a < 1)$ 图象交 $x$ 轴于点 $A$ ， $B$ ，交 $y$ 轴于点 $C$ ，与坐标圆的第四个交点为 $D$ ，连结 $P C$ ， $P D$ ，如图2.若 $∠ C P D = 120 °$ ，求 $a$ 的值.

查看试题解析