浙江省苍南县2021年数学初中毕业升学适应性试卷
试卷更新日期:2021-08-31 类型:中考模拟
一、单选题
-
1. 给出四个实数-2,-1,0, 其中最小的数是( )A、-2 B、-1 C、0 D、2. 某金属零件如图所示,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 计算 ,正确结果是( )A、 B、 C、 D、4. 若分式 的值为0,则x的值为( )A、3 B、-3 C、3或-3 D、05. 小南观察某个红绿灯口,发现红灯时间20秒,黄灯5秒,绿灯15秒,当他下次到达该路口时,遇到绿灯的概率是( )A、 B、 C、 D、6. 苍南县2020年下半年降雨最较少,校兴趣小组对这六个月下雨的天数进行记录,统计如下:
3. 计算 ,正确结果是( )A、 B、 C、 D、4. 若分式 的值为0,则x的值为( )A、3 B、-3 C、3或-3 D、05. 小南观察某个红绿灯口,发现红灯时间20秒,黄灯5秒,绿灯15秒,当他下次到达该路口时,遇到绿灯的概率是( )A、 B、 C、 D、6. 苍南县2020年下半年降雨最较少,校兴趣小组对这六个月下雨的天数进行记录,统计如下:月份(月)
七
八
九
十
十一
十二
雨天数(天)
13
13
14
5
7
14
则上表中下雨天数的中位数是( )
A、9.5天 B、10天 C、13天 D、13.5天7. 如图,在正方形方格纸中,每个小的四边形都是相同的正方形,点 , , , 都在格点处, 与 相交于点 ,则 的值是( ) A、 B、 C、 D、8. 如图, 中, ,分别以 、 为边作正方形 , , 交 于点 .若 ,则 的长为( )
A、 B、 C、 D、8. 如图, 中, ,分别以 、 为边作正方形 , , 交 于点 .若 ,则 的长为( )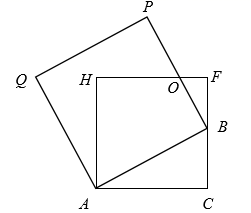 A、 B、 C、 D、9. 已知当自变量 在 的范围内时,二次函数 的最大值与最小值的差为4,则常数 的值可为( )A、-3 B、-1 C、1 D、310. 如图,矩形 的顶点 、 分别在反比例函数 与 的图象上,点 、 在 轴上, , 分别交 轴于点 、F,则阴影部分的面积为( )
A、 B、 C、 D、9. 已知当自变量 在 的范围内时,二次函数 的最大值与最小值的差为4,则常数 的值可为( )A、-3 B、-1 C、1 D、310. 如图,矩形 的顶点 、 分别在反比例函数 与 的图象上,点 、 在 轴上, , 分别交 轴于点 、F,则阴影部分的面积为( ) A、3 B、5 C、6 D、9
A、3 B、5 C、6 D、9二、填空题
-
11. 分解因式: = .12. 不等式组 的解是.13. 已知扇形的半径为4cm,圆心角为120°,则此扇形的弧长是 cm
14. 某餐厅供应单价为10元、18元、25元三种价格的快餐某月销售快餐情况的扇形统计图如图所示,则该餐厅这个月销售这三种快餐的平均单价为元.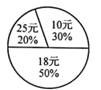 15. 如图,直线 : 交 轴于点 , 为 轴正半轴上一点, 轴交直线 于点 , , 交于点 ,记 的面积为 , 的面积为 ,当 时, 的长为.
15. 如图,直线 : 交 轴于点 , 为 轴正半轴上一点, 轴交直线 于点 , , 交于点 ,记 的面积为 , 的面积为 ,当 时, 的长为. 16. 如图1,这是一个装有货物的长方体形状的木箱沿着坡面装进汽车货箱的立体示意图,图2是它的平面示意图.已知汽车货箱高度 ,货箱底面距地面的高度 ,坡面与地面的夹角 ,木箱的长 为2m,高 为1.6m.宽小于汽车货箱的宽度.已知 ,木箱底部顶点C与坡面底部点 重合,则木箱底部悬空部分 的长为m,木箱上部顶点 到汽车货箱顶部 的距离为m.
16. 如图1,这是一个装有货物的长方体形状的木箱沿着坡面装进汽车货箱的立体示意图,图2是它的平面示意图.已知汽车货箱高度 ,货箱底面距地面的高度 ,坡面与地面的夹角 ,木箱的长 为2m,高 为1.6m.宽小于汽车货箱的宽度.已知 ,木箱底部顶点C与坡面底部点 重合,则木箱底部悬空部分 的长为m,木箱上部顶点 到汽车货箱顶部 的距离为m.
三、解答题
-
17.(1)、计算:(2)、化简:18. 如图,在四边形 中, ,点 为对角线 上一点, ,且 .
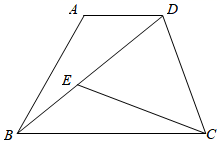 (1)、求证: .(2)、若 ,求 的度数.19. 如图所示,每个小正三角形的顶点叫做格点,各顶点在格点处的多边形称为格点多边形,线段 位于该小正三角形组成的网格中,按要求在网格中作一个格点多边形.
(1)、求证: .(2)、若 ,求 的度数.19. 如图所示,每个小正三角形的顶点叫做格点,各顶点在格点处的多边形称为格点多边形,线段 位于该小正三角形组成的网格中,按要求在网格中作一个格点多边形. (1)、请在图1中面一个以 为对角线的平行四边形 .(2)、请在图2中画一个以 为边的菱形 .20. 在体育课上,甲、乙两人各进行了5次的篮球测验(满分10分),老师对两人的成绩进行统计,如图所示.
(1)、请在图1中面一个以 为对角线的平行四边形 .(2)、请在图2中画一个以 为边的菱形 .20. 在体育课上,甲、乙两人各进行了5次的篮球测验(满分10分),老师对两人的成绩进行统计,如图所示. (1)、两人共10次的篮球测验成绩的众数是分;甲、乙两人中的篮球测验成绩较稳定.(2)、由于成绩不理想,甲乙两人各自需从A,B,C三个训练小组中随机选择一个小组参加训练,求甲、乙两人在同一个训练小组的概率.(要求列表或树状图)21. 如图,在平面直角坐标系中,抛物线 交 轴于点 , ,已知点 的坐标为 .
(1)、两人共10次的篮球测验成绩的众数是分;甲、乙两人中的篮球测验成绩较稳定.(2)、由于成绩不理想,甲乙两人各自需从A,B,C三个训练小组中随机选择一个小组参加训练,求甲、乙两人在同一个训练小组的概率.(要求列表或树状图)21. 如图,在平面直角坐标系中,抛物线 交 轴于点 , ,已知点 的坐标为 . (1)、求点 的坐标和抛物线的表达式.(2)、将抛物线顶点向上平移 个单位得点 ,过点 作 的平行线交抛物线于点 、 .若 ,求 的值.22. 如图, 为半圆 的直径, 为切线, 交半圆 于点 , 为 上一点,且 ,BE的延长线交 于点 ,连结 .
(1)、求点 的坐标和抛物线的表达式.(2)、将抛物线顶点向上平移 个单位得点 ,过点 作 的平行线交抛物线于点 、 .若 ,求 的值.22. 如图, 为半圆 的直径, 为切线, 交半圆 于点 , 为 上一点,且 ,BE的延长线交 于点 ,连结 .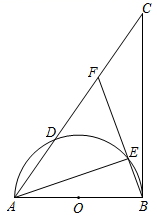 (1)、求证: .(2)、若 , ,求 的长.23. 某酒店新装修,计划购买A,B,C三种型号的餐桌共 套.已知一套A型餐桌(一桌四椅)需800元,一套B型餐桌(一桌六椅)需1000元,一套C型餐桌(一桌八椅)需1200元,要求购买C型餐桌的套数是A型餐桌的3倍,设购买 套A型餐桌,三种餐桌购买的总费用为 元.(1)、当 时,
(1)、求证: .(2)、若 , ,求 的长.23. 某酒店新装修,计划购买A,B,C三种型号的餐桌共 套.已知一套A型餐桌(一桌四椅)需800元,一套B型餐桌(一桌六椅)需1000元,一套C型餐桌(一桌八椅)需1200元,要求购买C型餐桌的套数是A型餐桌的3倍,设购买 套A型餐桌,三种餐桌购买的总费用为 元.(1)、当 时,①求 关于 的函数关系式.
②若购买的B型餐桌套数不多于C型餐桌套数,求总费用 的最小值,并写出此时具体的购买方案.
(2)、已知酒店实际购买三种餐桌的总费用为18万元,记购买的三种餐桌椅子的总数最多的方案为最佳购买方案,求最佳购买方案的椅子总数 及相应 的值.24. 如图,在 中, , 是边 上一动点,且不与 , 两点重合,连结 ,过点 作 交边 于点 , 的外接圆交边 于另一点 ,连结 .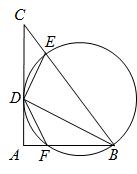 (1)、求证: .(2)、当 , 时.
(1)、求证: .(2)、当 , 时.①若 ,求 的长.
②当线段 , , 中有两条相等时,求出所有符合条件的 的值.
(3)、若 平分 , , ,则 .