新疆维吾尔自治区巴州区2021年数学中考一模试卷

试卷更新日期：2021-08-31 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2的绝对值是（）

A、﹣2 B、1 C、2 D、 $\frac{1}{2}$

查看试题解析
2. 2020年6月23日，北斗三号最后一颗全球组网卫星在西昌卫星发射中心成功发射并顺利进入预定轨道，它的稳定运行标志着全球四大卫星导航系统之一的中国北斗卫星导航系统全面建成.该卫星距离地面约36000千米，将数据36000用科学记数法表示为（）

A、 $3.6 \times 10^{3}$ B、 $3.6 \times 10^{4}$ C、 $3.6 \times 10^{5}$ D、 $36 \times 10^{4}$

查看试题解析
3. 下列计算正确的是（）

A、 $a^{8} \div a^{4} = a^{2}$ B、 ${(2 a^{2})}^{3} = 6 a^{6}$ C、 $3 a^{3} - 2 a^{2} = a$ D、 $3 a (1 - a) = 3 a - 3 a^{2}$

查看试题解析
4.
某运动会颁奖台如图所示，它的主视图是（）

A、 B、 C、 D、

查看试题解析
5. 如图，直线a∥b，将一个直角三角尺按如图所示的位置摆放，若∠1=58°，则∠2的度数为（）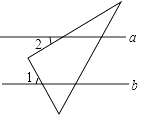

A、30° B、32° C、42° D、58°

查看试题解析
6.
如图，一辆小车沿倾斜角为α的斜坡向上行驶13米，已知cosα= $\frac{12}{13}$ ，则小车上升的高度是（）

A、5米 B、6米 C、6.5米 D、12米

查看试题解析
7. “今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”这是我国古代数学《九章算术》中的“井深几何”问题，它的题意可以由图获得，则井深为（）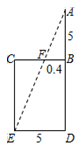

A、1.25尺 B、56.5尺 C、6.25尺 D、57.5尺

查看试题解析
8. 在一次学生田径运动会上.参加男子跳高的15名运动员的成绩如下表所示：

成绩（m）

1.50

1.60

1.65

1.70

1.75

1.80

人数

1

2

4

3

3

2

这些运动员跳高成绩的中位数和众数是（）

A、1.65，1.70 B、1.70，1.70 C、1.70，1.65 D、3，4

查看试题解析
9. 目前以 $5 G$ 等为代表的战略性新兴产业蓬勃发展.某市2019年底有 $5 G$ 用户2万户，计划到2021年底全市 $5 G$ 用户数累计达到8.72万户.设全市 $5 G$ 用户数年平均增长率为 $x$ ，则 $x$ 值为（）

A、 $20 %$ B、 $30 %$ C、 $40 %$ D、 $50 %$

查看试题解析
10. 如图，AB是⊙O的直径，CD是弦，∠BCD=30°，OA=2，则阴影部分的面积是（）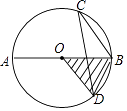

A、 $\frac{π}{3}$ B、 $\frac{2 π}{3}$ C、π D、2π

查看试题解析
11. 如图，在Rt△ABC中，AC=5cm，BC=12cm，∠ACB=90°，把Rt△ABC所在的直线旋转一周得到一个几何体，则这个几何体的侧面积为（）

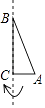A、60πcm² B、65πcm² C、120πcm² D、130πcm²

查看试题解析
12. 如图，抛物线y₁＝a（x+2）²﹣3与y₂＝ $\frac{1}{2}$ （x﹣3）²+1交于点A(1，3)，过点A作x轴的平行线，分别交两条抛物线于点B，C.则以下结论：①无论x取何值，y₂的值总是正数；②a＝ $\frac{2}{3}$ ；③当x＝0时，y₂﹣y₁＝6；④AB+AC＝10；其中正确结论的个数是（）

A、①②④ B、①③④ C、②③④ D、①②③④

查看试题解析

二、填空题

13. 分解因式： $2 a x^{2} - 8 a$ =.

查看试题解析
14. 如图，一组平行横格线，其相邻横格线间的距离都相等，已知点A、B、C、D、O都在横格线上，且线段AD，BC交于点O，则AB：CD等于．

查看试题解析
15. 对于一元二次方程 $x^{2} + b x + c = 0$ ，若 $b^{2} - 4 a c \geq 0$ ，则有 $x_{1} + x_{2} = - b$ ， $x_{1} x_{2} = c$ .方程 $x^{2} - 3 x + 2 = 0$ …①， $y^{2} - 4 y + 5 = 0$ …②所有根之和为.

查看试题解析
16. 平面直角坐标系xOy中，若抛物线y=ax²上的两点A、B满足OA=OB，且tan∠OAB= $\frac{1}{2}$ ，则称线段AB为该抛物线的通径．那么抛物线y= $\frac{1}{2}$ x²的通径长为．

查看试题解析
17. 一个盒子中装有 $10$ 个红球和若干个白球，这些求除颜色外都相同，再往该盒子中放入 $5$ 个相同的白球，摇匀后从中随机摸出一个球，若摸到白球的概率为 $\frac{5}{7}$ ，则盒子中原有的白球的个数为.

查看试题解析
18. 点P，Q，R在反比例函数 $y = \frac{k}{x}$ （常数k＞0，x＞0）图象上的位置如图所示，分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S₁ ， S₂ ， S₃.若OE＝ED＝DC，S₁＋S₃＝27，则S₂的值为.

查看试题解析

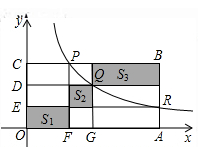
三、解答题

19.
①计算： $| \sqrt{2} - 1 | - \sqrt{8} + 2 \sin 45 ° + {(\frac{1}{2})}^{- 2}$

②解不等式组： ${\begin{array}{l} 4 (x - 1) \geq x + 2 \\ \frac{2 x + 1}{3} > x - 1 \end{array}$

③先化简，再求值： $\frac{x - 1}{x^{2} + 2 x + 1} \div (1 - \frac{2}{x + 1})$ ，其中 $x = \sqrt{3} - 1$ .

查看试题解析
20. 在如图的正方形网格中，每一个小正方形的边长为1.格点三角形ABC（顶点在格点上）顶点A、C的坐标分别是 $(- 4 ， 6)$ ， $(- 1 ， 4)$ .

（ 1 ）请在图中的网格平面内建立平面直角坐标系；

（ 2 ）请画出 $△ A B C$ 关于x轴对称的 $△ A_{1} B_{1} C_{1}$ ；

（ 3 ）请在y轴上求作一点P，使 $△ P B_{1} C$ 的周长最小，并写出点P的坐标和周长最小值.

查看试题解析
21. 2021年，成都将举办世界大学生运动会，这是在中国西部第一次举办的世界综合性运动会.目前，运动会相关准备工作正在有序进行，比赛项目已经确定.某校体育社团随机调查了部分同学在田径、跳水、篮球、游泳四种比赛项目中选择一种观看的意愿，并根据调查结果绘制成了如下两幅不完整的统计图.

根据以上信息，解答下列问题：

(1)、这次被调查的同学共有人；

(2)、扇形统计图中“篮球”对应的扇形圆心角的度数为；

(3)、现拟从甲、乙、丙、丁四人中任选两名同学担任大运会志愿者，请利用画树状图或列表的方法，求恰好选中甲、乙两位同学的概率.

查看试题解析
22. 某服装批发市场销售一种衬衫，衬衫每件进货价为50元，规定每件售价不低于进货价，经市场调查，每月的销售量 $y$ （件）与每件的售价 $x$ （元）满足一次函数关系，部分数据如下表：

售价 $x$ （元/件）

60

65

70

销售量 $y$ （件）

1400

1300

1200

(1)、求出 $y$ 与 $x$ 之间的函数表达式；（不需要求自变量 $x$ 的取值范围）

(2)、该批发市场每月想从这种衬衫销售中获利24000元，又想尽量给客户实惠，该如何给这种衬衫定价？

(3)、物价部门规定，该衬衫的每件利润不允许高于进货价的30%，设这种衬衫每月的总利润为 $w$ （元），那么售价定为多少元可获得最大利润？最大利润是多少？

查看试题解析
23. 如图，一辆轿车在一个十字路口遇到红灯刹车停下，轿车里的驾驶员看地面的斑马线前后两端的视角分别是 $∠ D C A = 30^{\circ}$ 和 $∠ D C B = 53^{\circ}$ ，如果斑马线的宽度 $A B = 4$ 米，驾驶员与车头的距离是1.8米，这时轿车车头与斑马线的距离 $x$ 约是多少米？（参考数据： $\sin 53^{\circ} \approx \frac{4}{5}$ ， $\cos 53^{\circ} \approx \frac{3}{5}$ ， $\tan 53^{\circ} \approx \frac{4}{3}$ ， $\sqrt{3} \approx 1.73$ ，结果精确到0.1米）

查看试题解析
24. 如图，已知AB是⊙O的直径，弦CD与直径AB相交于点F.点E在⊙O外，作直线AE，且∠EAC＝∠D.

(1)、求证：直线AE是⊙O的切线.

(2)、若∠BAC＝30°，BC＝4，cos∠BAD＝ $\frac{3}{4}$ ，CF＝ $\frac{10}{3}$ ，求BF的长.

查看试题解析
25. 如图，抛物线y＝－x²＋bx＋c与x轴相交于A（－1，0），B（5，0）两点．

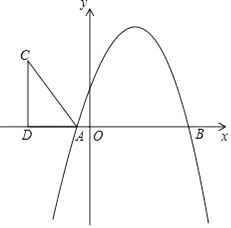(1)、求抛物线的解析式；

(2)、在第二象限内取一点C，作CD垂直x轴于点D，链接AC，且AD＝5，CD＝8，将Rt△ACD沿x轴向右平移m个单位，当点C落在抛物线上时，求m的值；

(3)、在（2）的条件下，当点C第一次落在抛物线上记为点E，点P是抛物线对称轴上一点．试探究：在抛物线上是否存在点Q，使以点B、E、P、Q为顶点的四边形是平行四边形？若存在，请出点Q的坐标；若不存在，请说明理由．

查看试题解析

售价 $x$ （元/件）	60	65	70
销售量 $y$ （件）	1400	1300	1200

成绩（m）	1.50	1.60	1.65	1.70	1.75	1.80
人数	1	2	4	3	3	2