四川省内江市市中区2021年数学中考适应性试卷
试卷更新日期:2021-08-31 类型:中考模拟
一、单选题
-
1. -2021的绝对值等于( )A、2021 B、-2021 C、 D、2. 嫦娥五号距离地球约160000公里,其中160000用科学记数法表示为( )A、16×104 B、1.6×104 C、1.6×105 D、0.16×1063. 如图所示放置的几何体,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列说法正确的是( )A、了解河南省初中生身高情况适宜全面调查 B、甲,乙两名射击运动员5次射击成绩的方差分别为s甲2=1.2,s乙2=2,说明甲的射击成绩比乙的射击成绩稳定 C、同旁内角互补是必然事件 D、已知某篮球运动员投篮投中的概率为0.6,则他投10次一定可投中6次5. 下列运算正确的是( )A、a2•a4=a8 B、(2a+b)(2a﹣b)=2a2﹣b2 C、(﹣a2)3=﹣a6 D、a4+a4=2a86. 若代数式 有意义,则实数x的取值范围是( )A、x>0 B、x≥0 C、x>0且x≠2 D、x≥0且x≠27. 如图,在▱ABCD中,AE= AD,连接BE,交AC于点F,AC=12,则AF为( )
4. 下列说法正确的是( )A、了解河南省初中生身高情况适宜全面调查 B、甲,乙两名射击运动员5次射击成绩的方差分别为s甲2=1.2,s乙2=2,说明甲的射击成绩比乙的射击成绩稳定 C、同旁内角互补是必然事件 D、已知某篮球运动员投篮投中的概率为0.6,则他投10次一定可投中6次5. 下列运算正确的是( )A、a2•a4=a8 B、(2a+b)(2a﹣b)=2a2﹣b2 C、(﹣a2)3=﹣a6 D、a4+a4=2a86. 若代数式 有意义,则实数x的取值范围是( )A、x>0 B、x≥0 C、x>0且x≠2 D、x≥0且x≠27. 如图,在▱ABCD中,AE= AD,连接BE,交AC于点F,AC=12,则AF为( )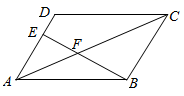 A、3 B、4 C、4.2 D、4.88. 关于 的一元二次方程 有实数根,则 满足( )A、 B、 且 C、 且 D、9. 如图, 为⊙ 的直径,C,D是圆周上的两点,若 ,则锐角 的度数为( )
A、3 B、4 C、4.2 D、4.88. 关于 的一元二次方程 有实数根,则 满足( )A、 B、 且 C、 且 D、9. 如图, 为⊙ 的直径,C,D是圆周上的两点,若 ,则锐角 的度数为( ) A、57° B、52° C、38° D、26°10. 《孙子算经》有一道题.大概意思是:用一根绳子去量一根木头的长,绳子还余 4.5 尺, 将绳子对折再量木头,则木头还剩余 1 尺,问木头长多少尺?可设木头为 x 尺,绳长为 y 尺,则所列方程组正确的是( )A、 B、 C、 D、11. 若关于x的一元一次不等式组 的解集为 ,且关于y的分式方程 的解为非正数,则符合条件的a所有整数的个数为( )A、2 B、3 C、4 D、512. 已知抛物线y=x2+(2m﹣6)x+m2﹣3与y轴交于点A,与直线x=4交于点B,当x 2时,y值随x值的增大而增大.记抛物线在线段AB下方的部分为G(包含A、B两点),M为G上任意一点,设M的纵坐标为t,若 ,则m的取值范围是( )A、m≥ B、 ≤m≤3 C、m≥3 D、1≤m≤3
A、57° B、52° C、38° D、26°10. 《孙子算经》有一道题.大概意思是:用一根绳子去量一根木头的长,绳子还余 4.5 尺, 将绳子对折再量木头,则木头还剩余 1 尺,问木头长多少尺?可设木头为 x 尺,绳长为 y 尺,则所列方程组正确的是( )A、 B、 C、 D、11. 若关于x的一元一次不等式组 的解集为 ,且关于y的分式方程 的解为非正数,则符合条件的a所有整数的个数为( )A、2 B、3 C、4 D、512. 已知抛物线y=x2+(2m﹣6)x+m2﹣3与y轴交于点A,与直线x=4交于点B,当x 2时,y值随x值的增大而增大.记抛物线在线段AB下方的部分为G(包含A、B两点),M为G上任意一点,设M的纵坐标为t,若 ,则m的取值范围是( )A、m≥ B、 ≤m≤3 C、m≥3 D、1≤m≤3二、填空题
-
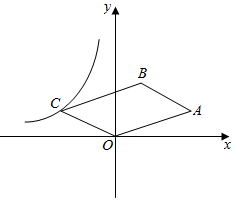
13. 分解因式:a2b-4b3=.14. 一组数据4,4,5,5,x,6,7的平均数是5,则这组数据的中位数是.15. 直角坐标系中,O(0,0),A(3,1),B(1,2).反比例函数y= (k≠0)的图象经过▱OABC的顶点C,则k=.
 16. 如图,等边△ABC的面积为 ,顺次连接△ABC各边的中点得△A1B1C1 , 顺次连接△A1B1C1各边的中点得△A2B2C2 , …,如此下去得△A2021B2021C2021 , 则△A2021B2021C2021的周长为.
16. 如图,等边△ABC的面积为 ,顺次连接△ABC各边的中点得△A1B1C1 , 顺次连接△A1B1C1各边的中点得△A2B2C2 , …,如此下去得△A2021B2021C2021 , 则△A2021B2021C2021的周长为.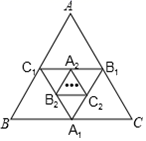 17. 已知实数x,y,z满足 ,则 的值为。18. 如图,平行四边形 的顶点A在x轴的正半轴上,点 在对角线 上,反比例函数 的图象经过C、D两点,已知平行四边形 的面积是 ,则点B的坐标为.
17. 已知实数x,y,z满足 ,则 的值为。18. 如图,平行四边形 的顶点A在x轴的正半轴上,点 在对角线 上,反比例函数 的图象经过C、D两点,已知平行四边形 的面积是 ,则点B的坐标为.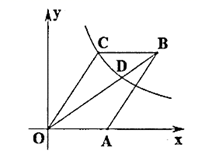 19. 如图,在矩形纸片ABCD中,AD=10,AB=8,将AB沿AE翻折,使点B落在 处,AE为折痕;再将EC沿EF翻折,使点C恰好落在线段EB'上的点 处,EF为折痕,连接 .若CF=3,则tan =.
19. 如图,在矩形纸片ABCD中,AD=10,AB=8,将AB沿AE翻折,使点B落在 处,AE为折痕;再将EC沿EF翻折,使点C恰好落在线段EB'上的点 处,EF为折痕,连接 .若CF=3,则tan =.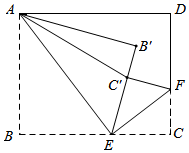 20. 如图,P为菱形ABCD内一动点,连接PA,PB,PD,∠APD=∠BAD=60°,AB=2,则PB+PD的最大值为.
20. 如图,P为菱形ABCD内一动点,连接PA,PB,PD,∠APD=∠BAD=60°,AB=2,则PB+PD的最大值为.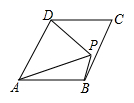
三、解答题
-
21. 计算: .22. 如图,在正方形 中,点 是 上的一点,点 是 延长线上的一点,且 ,连结 .
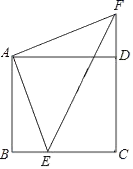 (1)、求证: ≌ ;(2)、若 ,请求出 的长.23. 为落实疫情期间的垃圾分类,树立全面环保意识,某校举行了“垃圾分类,绿色环保”知识竞赛活动,根据学生的成绩划分为 , , , 四个等级,并绘制了不完整的两种统计图:
(1)、求证: ≌ ;(2)、若 ,请求出 的长.23. 为落实疫情期间的垃圾分类,树立全面环保意识,某校举行了“垃圾分类,绿色环保”知识竞赛活动,根据学生的成绩划分为 , , , 四个等级,并绘制了不完整的两种统计图: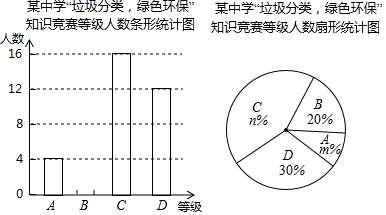
根据图中提供的信息,回答下列问题:
(1)、参加知识竞赛的学生共有 ▲ 人,并把条形统计图补充完整;(2)、扇形统计图中, , , 等级对应的圆心角为度;(3)、小明是四名获 等级的学生中的一位,学校将从获 等级的学生中任选取2人,参加市举办的知识竞赛,请用列表法或画树状图,求小明被选中参加区知识竞赛的概率.24. 如图,某数学兴趣小组为测量一颗古树BH和教学楼CG的高,先在A处用高1.5米的测角仪AF测得古树顶端H的仰角 为 ,此时教学楼顶端G恰好在视线FH上,再向前走10米到达B处,又测得教学楼顶端G的仰角 为 ,点A、B、C三点在同一水平线上.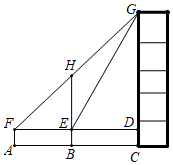 (1)、求古树BH的高;(2)、求教学楼CG的高.(参考数据: )
(1)、求古树BH的高;(2)、求教学楼CG的高.(参考数据: )四、拓展探索题
-
25. 如图,直线 与双曲线 在第一象限内交于A、B两点,已知 , .
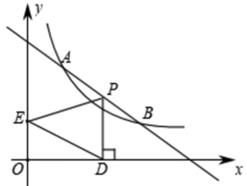 (1)、求 的值及直线 的解析式.(2)、根据函数图象,直接写出不等式 的解集.(3)、设点P是线段 上的一个动点,过点P作 轴于点D,E是y轴上一点,当 的面积最大时,请求出此时P点的坐标.26. 阅读与应用:
(1)、求 的值及直线 的解析式.(2)、根据函数图象,直接写出不等式 的解集.(3)、设点P是线段 上的一个动点,过点P作 轴于点D,E是y轴上一点,当 的面积最大时,请求出此时P点的坐标.26. 阅读与应用:阅读1:a、b为实数,且a>0,b>0,因为 ,所以 ,从而 (当a=b时取等号).
阅读2:函数 (常数m>0,x>0),由阅读1结论可知: ,所以当 即 时,函数 的最小值为 .
阅读理解上述内容,解答下列问题:
(1)、已知一个矩形的面积为4,其中一边长为x,则另一边长为 ,周长为 ,求当x=时,周长的最小值为.(2)、已知函数y1=x+1(x>-1)与函数y2=x2+2x+17(x>-1),当x=时, 的最小值为.(3)、某民办学习每天的支出总费用包含以下三个部分:一是教职工工资6400元;二是学生生活费每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)27. 如图,BC是⊙O的直径,AD是⊙O的弦,AD交BC于点E,连接AB,CD,过点E作EF⊥AB,垂足为F,∠AEF=∠D.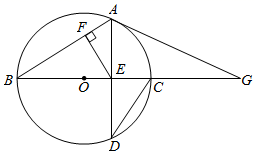 (1)、求证:AD⊥BC;(2)、点G在BC的延长线上,连接AG,∠DAG=2∠D.
(1)、求证:AD⊥BC;(2)、点G在BC的延长线上,连接AG,∠DAG=2∠D.①求证:AG与⊙O相切;
②当 ,CE=4时,直接写出CG的长.
28. 如图1,抛物线y=﹣x2+bx+c过点A(﹣1,0),点B(3,0)与y轴交于点C . 在x轴上有一动点E(m , 0)(0 m 3),过点E作直线l⊥x轴,交抛物线于点M .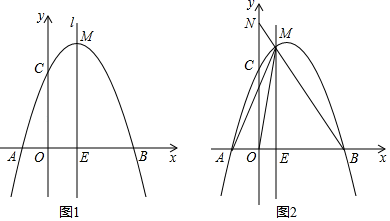 (1)、求抛物线的解析式及C点坐标;(2)、当m=1时,D是直线l上的点且在第一象限内,若△ACD是以∠DCA为底角的等腰三角形,求点D的坐标;(3)、如图2,连接BM并延长交y轴于点N , 连接AM , OM , 设△AEM的面积为S1 , △MON的面积为S2 , 若S1=2S2 , 求m的值.
(1)、求抛物线的解析式及C点坐标;(2)、当m=1时,D是直线l上的点且在第一象限内,若△ACD是以∠DCA为底角的等腰三角形,求点D的坐标;(3)、如图2,连接BM并延长交y轴于点N , 连接AM , OM , 设△AEM的面积为S1 , △MON的面积为S2 , 若S1=2S2 , 求m的值.