陕西省西安市莲湖区2021年数学中考二模试卷
试卷更新日期:2021-08-31 类型:中考模拟
一、单选题
-
1. 计算 的结果是( )A、2021 B、1 C、0 D、2. 下列图形中可以作为一个三棱柱的展开图的是( )A、
 B、
B、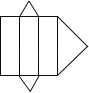 C、
C、 D、
D、 3. 2020年,陕西省实现社会消费品零售总额9605.92亿元,将数字9605.92亿用科学记数法表示为( )A、 B、 C、 D、4. 如图,直线 与 相交于点O, 与 互余, ,则 的度数是( )
3. 2020年,陕西省实现社会消费品零售总额9605.92亿元,将数字9605.92亿用科学记数法表示为( )A、 B、 C、 D、4. 如图,直线 与 相交于点O, 与 互余, ,则 的度数是( )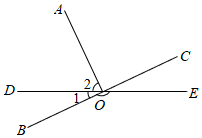 A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 在平面直角坐标系中,将直线 先向左平移2个单位长度,再向上平移5个单位长度,则平移后的新直线为( )A、 B、 C、 D、7. 如图,在 中,M,N是 上两点, ,连接 , , , ,添加一个条件,使四边形 是菱形,这个条件是( )
A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 在平面直角坐标系中,将直线 先向左平移2个单位长度,再向上平移5个单位长度,则平移后的新直线为( )A、 B、 C、 D、7. 如图,在 中,M,N是 上两点, ,连接 , , , ,添加一个条件,使四边形 是菱形,这个条件是( )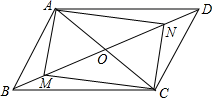 A、 B、 C、 D、8. 如图, 是 的内接三角形,作 与 相交于点C,且 ,则 的大小为( )
A、 B、 C、 D、8. 如图, 是 的内接三角形,作 与 相交于点C,且 ,则 的大小为( ) A、 B、 C、 D、9. 如图的网格中,每个小正方形的边长为1,A,B,C三点均在格点上,结论错误的是( )
A、 B、 C、 D、9. 如图的网格中,每个小正方形的边长为1,A,B,C三点均在格点上,结论错误的是( )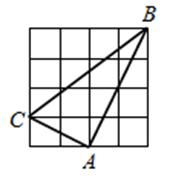 A、AB=2 B、∠BAC=90° C、 D、点A到直线BC的距离是210. 若抛物线 的对称轴为直线 ,且该抛物线与x轴交于A、B两点,若 的长是6,则该抛物线的顶点坐标为( )A、 B、 C、 D、
A、AB=2 B、∠BAC=90° C、 D、点A到直线BC的距离是210. 若抛物线 的对称轴为直线 ,且该抛物线与x轴交于A、B两点,若 的长是6,则该抛物线的顶点坐标为( )A、 B、 C、 D、二、填空题
-
11. 比较大小: .(填“>”、“<”或“=”)12. 圆内接正六边形的边长为6,则该正六边形的边心距为.13. 如图, 的顶点O在坐标原点上, ,若点B在反比例函数 的图象上,点A在反比例函数 的图象上,则k的值为.
 14. 如图,在正方形 中,以 为边,在正方形 内部作等边三角形△ ,点P在对角线 上,且 ,则 的最小值为.
14. 如图,在正方形 中,以 为边,在正方形 内部作等边三角形△ ,点P在对角线 上,且 ,则 的最小值为.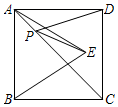
三、解答题
-
15. 计算: .16. 化简: .17. 如图,在 中.请用尺规作图法,求作一个以 为内角的菱形 ,使顶点E、F、G分别在 、 、 边上.
 18. 如图, , , .求证: .
18. 如图, , , .求证: . 19. 第十四届全运会圣火将在西安点燃,西安将再次惊艳全国.2019年8月2日,“朱朱”“熊熊”“羚羚”“金金”问世,成为2021年第十四届全国运动会的吉祥物.某校为了让学生进一步了解2021年“吉祥物”相关知识,计划开展“吉祥物知识进课堂”活动,开展活动之前,学校老师随机抽取若干名学生,对“你最感兴趣的吉祥物”进行了调查,经调查统计,结合学生自身的兴趣,每人从“A.朱朱、B.熊熊、C.羚羚、D.金金”中选择一项.现将调查结果绘制成如下两幅不完整的统计图.结合图中信息解答下列问题:
19. 第十四届全运会圣火将在西安点燃,西安将再次惊艳全国.2019年8月2日,“朱朱”“熊熊”“羚羚”“金金”问世,成为2021年第十四届全国运动会的吉祥物.某校为了让学生进一步了解2021年“吉祥物”相关知识,计划开展“吉祥物知识进课堂”活动,开展活动之前,学校老师随机抽取若干名学生,对“你最感兴趣的吉祥物”进行了调查,经调查统计,结合学生自身的兴趣,每人从“A.朱朱、B.熊熊、C.羚羚、D.金金”中选择一项.现将调查结果绘制成如下两幅不完整的统计图.结合图中信息解答下列问题: (1)、请将两幅统计图补充完整,所抽取学生最感兴趣的吉祥物是 ▲ ;(2)、在这次调查中,A、B、C、D哪项选择人数少于调查总人数的平均数?(3)、若本校一共有2000名学生,请估计“对B.熊熊最感兴趣”的人数.20. 在学习了相似三角形的应用知识点后,小丽为了测量某建筑 的高度,在地面上的点D与同学们一同竖直放了一根标杆 ,并在地面上放置一块平面镜E,已知建筑底端B、E、D点在同一条水平直线上,在标杆顶端点C恰好通过平面镜E观测到建筑顶点A,在点C观测建筑顶点A的仰角为 ,平面镜E的俯角为 ,其中标杆 的长度为1米,问建筑 的高度为多少米?(结果精确到0.1米,参考数据: )
(1)、请将两幅统计图补充完整,所抽取学生最感兴趣的吉祥物是 ▲ ;(2)、在这次调查中,A、B、C、D哪项选择人数少于调查总人数的平均数?(3)、若本校一共有2000名学生,请估计“对B.熊熊最感兴趣”的人数.20. 在学习了相似三角形的应用知识点后,小丽为了测量某建筑 的高度,在地面上的点D与同学们一同竖直放了一根标杆 ,并在地面上放置一块平面镜E,已知建筑底端B、E、D点在同一条水平直线上,在标杆顶端点C恰好通过平面镜E观测到建筑顶点A,在点C观测建筑顶点A的仰角为 ,平面镜E的俯角为 ,其中标杆 的长度为1米,问建筑 的高度为多少米?(结果精确到0.1米,参考数据: ) 21. 为进一步落实精准扶贫工作.某农科所李教授选择乘坐客车前往目的地.经了解,长途汽车客运站规定乘客可以免费携带一定质量的行李,若携带行李质量超出免费的范围.乘客需自行购买行李票,行李票y(元)与行李质量x(千克)之间的关系如图所示.
21. 为进一步落实精准扶贫工作.某农科所李教授选择乘坐客车前往目的地.经了解,长途汽车客运站规定乘客可以免费携带一定质量的行李,若携带行李质量超出免费的范围.乘客需自行购买行李票,行李票y(元)与行李质量x(千克)之间的关系如图所示. (1)、求y与x之间的函数表达式,并直接写出x的取值范围.(2)、当李教授携带72千克行李时,行李费需要多少钱?22. 小红和小兵进行摸球试验,在一个不透明的空布袋中放有4个小球.分别标号1,2,3,4,小球除数字不同外其他都相同.试验规则:摸球前先搅拌均匀,每次随机摸一个小球,记下数字后,称为摸球一次.(1)、若小兵随机摸球一次,摸到标号为奇数的概率为;(2)、若小红从袋中不放回地随机摸两次,请用列表法或画树状图法求出两球标号均为偶数的概率.23. 如图, 为 的直径, 、 是 的两条弦, 是 的切线,且 交 于点D.
(1)、求y与x之间的函数表达式,并直接写出x的取值范围.(2)、当李教授携带72千克行李时,行李费需要多少钱?22. 小红和小兵进行摸球试验,在一个不透明的空布袋中放有4个小球.分别标号1,2,3,4,小球除数字不同外其他都相同.试验规则:摸球前先搅拌均匀,每次随机摸一个小球,记下数字后,称为摸球一次.(1)、若小兵随机摸球一次,摸到标号为奇数的概率为;(2)、若小红从袋中不放回地随机摸两次,请用列表法或画树状图法求出两球标号均为偶数的概率.23. 如图, 为 的直径, 、 是 的两条弦, 是 的切线,且 交 于点D.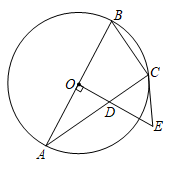 (1)、求证: .(2)、若 的半径为8, ,求弦 的长.24. 如图,抛物线 : 与抛物线 : 关于y轴对称, 与x轴交于A,B两点,其中点A在点B的左侧.
(1)、求证: .(2)、若 的半径为8, ,求弦 的长.24. 如图,抛物线 : 与抛物线 : 关于y轴对称, 与x轴交于A,B两点,其中点A在点B的左侧. (1)、求抛物线 , 的函数表达式.(2)、在抛物线 上是否存在一点N,在抛物线 上是否存在一点M,使得以 为边,且以A、B、M、N四点为顶点的四边形是平行四边形?若存在,求出M、N两点的坐标;若不存在,请说明理由.25. 如图
(1)、求抛物线 , 的函数表达式.(2)、在抛物线 上是否存在一点N,在抛物线 上是否存在一点M,使得以 为边,且以A、B、M、N四点为顶点的四边形是平行四边形?若存在,求出M、N两点的坐标;若不存在,请说明理由.25. 如图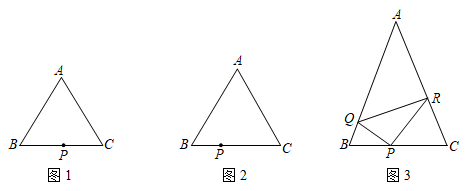 (1)、如图1,在等边 中, .点P、D、E分别为边 、 、 上(均不与端点重合)的动点.
(1)、如图1,在等边 中, .点P、D、E分别为边 、 、 上(均不与端点重合)的动点.①当点P为 的中点时,在图1中,作出 ,使 的周长最小,并直接写出 的周长的最小值;
②如图2,当 时,求 的周长的最小值.
(2)、如图3,在等腰 中. , , ,点P、Q、R分别为边 、 、 上(均不与端点重合)的动点,求 周长的最小值并简要说明理由.