2021年苏科版数学八年级上册1.3 探索三角形全等的条件——SAS 同步练习(提优版)
试卷更新日期:2021-08-31 类型:同步测试
一、单选题
-
1. 如图,已知AD=AE,BE=CD,∠1=∠2=100°,若∠BAE=60°,则∠CAE的度数为( )
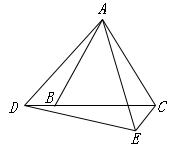
 A、40° B、60° C、80° D、100°2. 如图,△ABD与△ACE均为正三角形,且AB<AC,则BE与CD之间的大小关系是( )
A、40° B、60° C、80° D、100°2. 如图,△ABD与△ACE均为正三角形,且AB<AC,则BE与CD之间的大小关系是( ) A、BE=CD B、BE>CD C、BE<CD D、大小关系不确定3. 如图,△ABC中,∠ABC=∠ACB,D为BC上一点,BF=CD,CE=BD,则∠EDF等于( )
A、BE=CD B、BE>CD C、BE<CD D、大小关系不确定3. 如图,△ABC中,∠ABC=∠ACB,D为BC上一点,BF=CD,CE=BD,则∠EDF等于( ) A、 B、 C、 D、4. 如图,AD是△ABC的中线,E、F分别在AB、AC上,且DE⊥DF,则( )
A、 B、 C、 D、4. 如图,AD是△ABC的中线,E、F分别在AB、AC上,且DE⊥DF,则( ) A、BE+CF>EF B、BE+CF=EF C、BE+CF<EF D、BE+CF与EF的大小关 系不能确定.5. 在图3所示的3×3正方形网格中,∠1+∠2+∠3+∠4+∠5等于( ).
A、BE+CF>EF B、BE+CF=EF C、BE+CF<EF D、BE+CF与EF的大小关 系不能确定.5. 在图3所示的3×3正方形网格中,∠1+∠2+∠3+∠4+∠5等于( ). A、145° B、180° C、225° D、270°6. 如图,边长相等的两个正方形ABCD和OEFG,若将正方形OEFG绕点O按逆时针方向旋转150°,两个正方形的重叠部分四边形OMCN的面积( )
A、145° B、180° C、225° D、270°6. 如图,边长相等的两个正方形ABCD和OEFG,若将正方形OEFG绕点O按逆时针方向旋转150°,两个正方形的重叠部分四边形OMCN的面积( ) A、不变 B、先增大再减小 C、先减小再增大 D、不断增大7. 如图,以▱ABCD 的四条边为边,分别向外作正方形,连结 EF,GH,IJ,KL.如果▱ABCD 的 面积为 8,则图中阴影部分四个三角形的面积和为( )
A、不变 B、先增大再减小 C、先减小再增大 D、不断增大7. 如图,以▱ABCD 的四条边为边,分别向外作正方形,连结 EF,GH,IJ,KL.如果▱ABCD 的 面积为 8,则图中阴影部分四个三角形的面积和为( ) A、8 B、12 C、16 D、208. 如图1、2、3中,点 、 分别是正 、正方形 、正五边形 中以 点为顶点的相邻两边上的点,且 , 交 于 点, 的度数分别为 , , ,若其余条件不变,在正九边形 中, 的度数是( )
A、8 B、12 C、16 D、208. 如图1、2、3中,点 、 分别是正 、正方形 、正五边形 中以 点为顶点的相邻两边上的点,且 , 交 于 点, 的度数分别为 , , ,若其余条件不变,在正九边形 中, 的度数是( ) A、 B、 C、 D、9. 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=4,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( )
A、 B、 C、 D、9. 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=4,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( ) A、 B、 C、1 D、10. 如图,△ABC中,AB=AC,D、E分别在CA、BA的延长线上,连接BD、CE,且∠D+∠E=180°,若BD=6,则CE的长为( )
A、 B、 C、1 D、10. 如图,△ABC中,AB=AC,D、E分别在CA、BA的延长线上,连接BD、CE,且∠D+∠E=180°,若BD=6,则CE的长为( )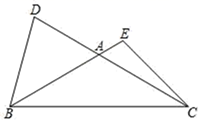 A、6 B、5 C、3 D、4.5
A、6 B、5 C、3 D、4.5二、填空题
-
11. 如图,已知 ,要用 判断 ≌ ,需增加一个条件: .
 12. 已知BD为四边ABCD的对角线,AB∥CD,要使△ABD≌△CDB,利用“SAS”可加条件 .
12. 已知BD为四边ABCD的对角线,AB∥CD,要使△ABD≌△CDB,利用“SAS”可加条件 .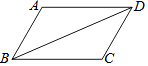 13. 如图,点B、F、C、E在一条直线上,已知FB=CE,AC∥DF,请你添加一个适当的条件能用SAS说明△ABC≌△DEF.
13. 如图,点B、F、C、E在一条直线上,已知FB=CE,AC∥DF,请你添加一个适当的条件能用SAS说明△ABC≌△DEF. 14. 如图,在等边三角形 ABC 中,点 D,E 分别在边 BC,AC 上,且 BD=CE,AD 与 BE相交于点 P,则∠APE 的度数为.
14. 如图,在等边三角形 ABC 中,点 D,E 分别在边 BC,AC 上,且 BD=CE,AD 与 BE相交于点 P,则∠APE 的度数为. 15. 如图,在△ABC和△DBC中,∠A=40°,AB=AC=2,∠BDC=140°,BD=CD,以点D为顶点作∠MDN=70°,两边分别交AB,AC于点M,N,连接MN,则△AMN的周长为 .
15. 如图,在△ABC和△DBC中,∠A=40°,AB=AC=2,∠BDC=140°,BD=CD,以点D为顶点作∠MDN=70°,两边分别交AB,AC于点M,N,连接MN,则△AMN的周长为 . 16. 在△ABC中,AB=4,AC=6,D为BC边的中点,则中线AD的取值范围是 .17. 等边△ACD和等边△BCE有一个公共顶点C,直线AE与BD交于点F ,直线AE与CD交于点G, 直线CE与BD交于点H,连接GH. 下列结论:①AE=DB;②△BHC≌△EGC;③∠DFA=60°;④△HGC为等边三角形. 其中正确的结论有.(填序号)
16. 在△ABC中,AB=4,AC=6,D为BC边的中点,则中线AD的取值范围是 .17. 等边△ACD和等边△BCE有一个公共顶点C,直线AE与BD交于点F ,直线AE与CD交于点G, 直线CE与BD交于点H,连接GH. 下列结论:①AE=DB;②△BHC≌△EGC;③∠DFA=60°;④△HGC为等边三角形. 其中正确的结论有.(填序号)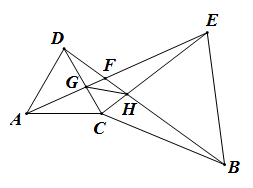 18. 如图,△ABC是等边三角形,且AB=1,点M为直线BC上的一个动点,连接AM,将线段AM绕A点顺时针旋转60°至AD,点N为直线AC上的一个动点,则D、N两点间距离的最小值为.
18. 如图,△ABC是等边三角形,且AB=1,点M为直线BC上的一个动点,连接AM,将线段AM绕A点顺时针旋转60°至AD,点N为直线AC上的一个动点,则D、N两点间距离的最小值为.
三、解答题
-
19. 如图,已知△ABC和△BDE都是等边三角形,且A,E,D三点在一直线上.请你说明DA﹣DB=DC.
 20. 如图,已知 中, , , 是 上一点, 在 的延长线上,且 , 的延长线与 交于点 .求证: .
20. 如图,已知 中, , , 是 上一点, 在 的延长线上,且 , 的延长线与 交于点 .求证: . 21. 已知如图等边三角形△ABC,D,E分别是BC,AC上的点.AD、BE交于点N,BM⊥AD于M.若AE=CD,求证:MN= BN.
21. 已知如图等边三角形△ABC,D,E分别是BC,AC上的点.AD、BE交于点N,BM⊥AD于M.若AE=CD,求证:MN= BN. 22. 如图, 均为等腰直角三角形,连接AE,CD,AE与CD相等吗?说明理由
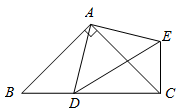
22. 如图, 均为等腰直角三角形,连接AE,CD,AE与CD相等吗?说明理由 23. △ABC是等腰直角三角形,其中CA=CB,四边形CDEF是正方形,连接AF,BD.观察图形,猜想AF与BD之间的数量和位置关系,并证明你的猜想
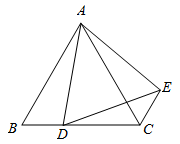
23. △ABC是等腰直角三角形,其中CA=CB,四边形CDEF是正方形,连接AF,BD.观察图形,猜想AF与BD之间的数量和位置关系,并证明你的猜想 24. 如图,在等边△ABC中,点D为BC边上的一点,在等边△ABC的外角平分线CE上取一点E,使CE=BD,连接AE、DE,请判断△ADE的形状,并说明理由.
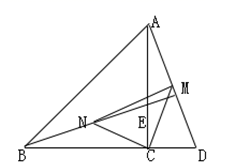
24. 如图,在等边△ABC中,点D为BC边上的一点,在等边△ABC的外角平分线CE上取一点E,使CE=BD,连接AE、DE,请判断△ADE的形状,并说明理由. 25. 如图:在ΔABC中,∠ACB= ,AC=BC,D在BC延长线上,E是AC上一点,且EC=DC,M、N分别是AD、BE的中点,判断ΔMCN形状并证明.
25. 如图:在ΔABC中,∠ACB= ,AC=BC,D在BC延长线上,E是AC上一点,且EC=DC,M、N分别是AD、BE的中点,判断ΔMCN形状并证明.