初中数学湘教版八年级上册2.1三角形 同步练习
试卷更新日期:2021-08-31 类型:同步测试
一、单选题
-
1. 若下列各组数值代表三根木棒的长度,则不能用它们摆成三角形的是( )A、3cm,4cm,5cm B、8cm,8cm,14cm C、6cm,7cm,11cm D、1cm,2cm,4cm2. 在三角形中,一定能将其面积分成相等两部分的是( )A、中线 B、高线 C、角平分线 D、某一边的垂直平分线3. 如图,∠A、∠1、∠2的大小关系是( )
 A、∠A>∠1>∠2 B、∠2>∠1>∠A C、∠A>∠2>∠1 D、∠2>∠A>∠14. 将长为12的线段截成长度为整数的三段,使它们成为一个三角形的三边,则构成的三角形不可能是( )A、等腰三角形 B、钝角三角形 C、等边三角形 D、直角三角形5. 如图所示,工人师傅在砌门时,通常用木条BD固定长方形门框ABCD , 使其不变形这样做的数学根据是( )
A、∠A>∠1>∠2 B、∠2>∠1>∠A C、∠A>∠2>∠1 D、∠2>∠A>∠14. 将长为12的线段截成长度为整数的三段,使它们成为一个三角形的三边,则构成的三角形不可能是( )A、等腰三角形 B、钝角三角形 C、等边三角形 D、直角三角形5. 如图所示,工人师傅在砌门时,通常用木条BD固定长方形门框ABCD , 使其不变形这样做的数学根据是( )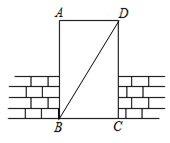 A、三角形具有稳定性 B、两点之间,线段最短 C、对顶角相等 D、垂线段最短6. 在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A、
A、三角形具有稳定性 B、两点之间,线段最短 C、对顶角相等 D、垂线段最短6. 在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A、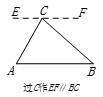 B、
B、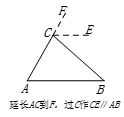 C、
C、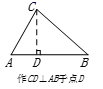 D、
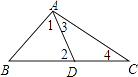
D、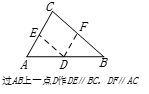 7. 如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=105°,则∠DAC的度数为( )
7. 如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=105°,则∠DAC的度数为( ) A、80° B、82° C、84° D、86°8. 如图,△ABC中,∠ACB=90°,D为AB上任一点,过D作AB的垂线,分别交边AC、BC的延长线于EF两点,∠BAC∠BFD的平分线交于点I,AI交DF于点M,FI交AC于点N,连接BI.下列结论:①∠BAC=∠BFD;②∠ENI=∠EMI;③AI⊥FI;④∠ABI=∠FBI;其中正确结论的个数是( )
A、80° B、82° C、84° D、86°8. 如图,△ABC中,∠ACB=90°,D为AB上任一点,过D作AB的垂线,分别交边AC、BC的延长线于EF两点,∠BAC∠BFD的平分线交于点I,AI交DF于点M,FI交AC于点N,连接BI.下列结论:①∠BAC=∠BFD;②∠ENI=∠EMI;③AI⊥FI;④∠ABI=∠FBI;其中正确结论的个数是( )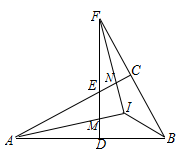 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 在Rt△ABC中,∠C=90°,AC=9,AB=15,则点C到AB的距离是 .10. 一张小凳子的结构如图所示, ,若 ,则 的度数为.
 11. 已知 的三边长为2,7, ,请写出一个符合条件的 的整数值,这个值可以是.12. 如果三角形的一个外角等于与它相邻的内角的5倍,等于与它不相邻的一个内角的3倍.则此三角形最大内角是度.13. 如图,要使五边形木架不变形,至少要再钉上根木条.
11. 已知 的三边长为2,7, ,请写出一个符合条件的 的整数值,这个值可以是.12. 如果三角形的一个外角等于与它相邻的内角的5倍,等于与它不相邻的一个内角的3倍.则此三角形最大内角是度.13. 如图,要使五边形木架不变形,至少要再钉上根木条. 14. 如图, 的 和 的平分线 , 相交于点 ,若 ,则 的度数为 .
14. 如图, 的 和 的平分线 , 相交于点 ,若 ,则 的度数为 .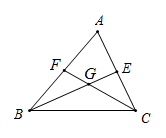
三、计算题
-
15. 若a,b,c是△ABC的三边的长,化简|a-b-c|+|b-c-a|+|c+a-b|.16. 如图,在△ABC中,D是BC上的一点,∠1=∠2,∠3=∠4,∠B=40°,求∠BAC的度数.
 17. 如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠B=60°,求∠A的度数.
17. 如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠B=60°,求∠A的度数.
四、解答题
-
18. 如图,每个小方格的边长都为1.求图中格点四边形ABCD的面积.
 19. 如图, 中, 平分 , 为 延长线上一点, 于点 ,若 , ,求 的度数.
19. 如图, 中, 平分 , 为 延长线上一点, 于点 ,若 , ,求 的度数. 20. 在 中,已知 ,若第三边 的长为偶数,求 的周长.21. 如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=50°,求∠EAD的度数.
20. 在 中,已知 ,若第三边 的长为偶数,求 的周长.21. 如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=50°,求∠EAD的度数.
五、作图题
-
22. 在如图所示的正方形网格中,每个小方格的边长为 1,点 A、B、C 是格点.(1)、只用直尺(不带刻度)作出AB边上的高CH(保留作图痕迹);
 (2)、只用直尺(不带刻度)作出AC边上的高BG(保留作图痕迹).
(2)、只用直尺(不带刻度)作出AC边上的高BG(保留作图痕迹). 23. 如图:在正方形网格中有一个△ABC,请按下列要求进行(借助于网格)
23. 如图:在正方形网格中有一个△ABC,请按下列要求进行(借助于网格) (1)、请作出△ABC中BC边上的中线AD;(2)、请作出△ABC中AB边上的高CE;
(1)、请作出△ABC中BC边上的中线AD;(2)、请作出△ABC中AB边上的高CE;六、综合题
-
24. 如图,AD,CE是△ABC的两条高;已知AD=10,CE=9,AB=12.
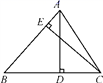 (1)、求△ABC的面积;(2)、求BC的长.25. “佳园工艺店”打算制作一批有两边长分别是7分米,3分米,第三边长为奇数(单位:分米)的不同规格的三角形木框.(1)、要制作满足上述条件的三角形木框共有种.(2)、若每种规格的三角形木框只制作一个,制作这种木框的木条的售价为8元╱分米,问至少需要多少钱购买材料?(忽略接头)26. 阅读下列材料并解答问题:在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“梦想三角形”例如:一个三角形三个内角的度数分别是 , , ,这个三角形就是一个“梦想三角形”.反之,若一个三角形是“梦想三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.
(1)、求△ABC的面积;(2)、求BC的长.25. “佳园工艺店”打算制作一批有两边长分别是7分米,3分米,第三边长为奇数(单位:分米)的不同规格的三角形木框.(1)、要制作满足上述条件的三角形木框共有种.(2)、若每种规格的三角形木框只制作一个,制作这种木框的木条的售价为8元╱分米,问至少需要多少钱购买材料?(忽略接头)26. 阅读下列材料并解答问题:在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“梦想三角形”例如:一个三角形三个内角的度数分别是 , , ,这个三角形就是一个“梦想三角形”.反之,若一个三角形是“梦想三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍. (1)、如果一个“梦想三角形”有一个角为 ,那么这个“梦想三角形”的最小内角的度数为.(2)、如图,已知 ,在射线 上取一点A,过点A作 交 于点B,以A为端点作射线 ,交线段 于点C(点C不与O、B重合),若 ,判定 、 是否是“梦想三角形”,为什么?27. 已知 的面积是 ,请完成下列问题:
(1)、如果一个“梦想三角形”有一个角为 ,那么这个“梦想三角形”的最小内角的度数为.(2)、如图,已知 ,在射线 上取一点A,过点A作 交 于点B,以A为端点作射线 ,交线段 于点C(点C不与O、B重合),若 ,判定 、 是否是“梦想三角形”,为什么?27. 已知 的面积是 ,请完成下列问题: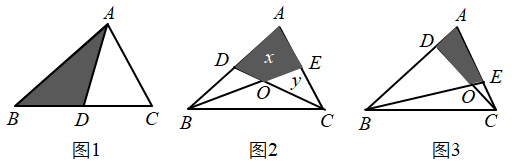 (1)、如图1所示,若 是 的 边上的中线,则 的面积 的面积.(填“ ”“ ”或“ ”)(2)、如图2所示,若 , 分别是 的 , 边上的中线,求四边形 的面积可以用如下方法:连接 ,由 得: ,同理: ,设 , 则 , .由题意得: , ,可列方程组为 ,解得 , 通过解这个方程组可得四边形 的面积为 .(3)、如图3所示, , ,请你计算四边形 的面积,并说明理由.
(1)、如图1所示,若 是 的 边上的中线,则 的面积 的面积.(填“ ”“ ”或“ ”)(2)、如图2所示,若 , 分别是 的 , 边上的中线,求四边形 的面积可以用如下方法:连接 ,由 得: ,同理: ,设 , 则 , .由题意得: , ,可列方程组为 ,解得 , 通过解这个方程组可得四边形 的面积为 .(3)、如图3所示, , ,请你计算四边形 的面积,并说明理由.