2021年苏科版数学八年级上册 1.3 探索三角形全等的条件——SAS 同步练习 （基础版）
试卷更新日期：2021-08-31 类型：同步测试
一、单选题
-
1. 如图，下列三角形中全等的是（ ）
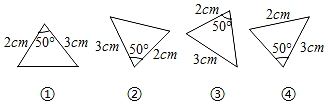A、①② B、②③ C、③④ D、①④2. 如图，将两根钢条AA'、BB’的中点O连在一起，使AA’、BB'能绕着点O自由转动，就做成了一个测量工具，由三角形全等可知A'B'的长等于内槽宽AB，那么判定△OAB≌△OA' B'的理由是（ ）
A、SAS B、ASA C、SSS D、AAS3. 如图，已知 ，能直接用 证明 的条件是（ ）.
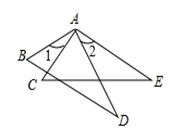
A、 B、 C、 D、4. 如图，已知∠1=∠2，若用“SAS”证明△ACB≌△BDA，还需加上条件（ ）
A、AD ＝BC B、BD＝AC C、∠D＝∠C D、OA＝OB5. 如图，在△ABC中，AB＝AC，BE， CF是中线，判定△AFC≌△AEB的方法是（ ）
A、SSS B、SAS C、AAS D、HL6. 如图，AC与BD交于O点，若 ，用“SAS”证明 ≌ ，还需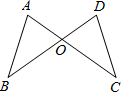
A、 B、 C、 D、7. 如图，AB＝AC，点D、E分别是AB、AC上一点，AD＝AE，BE、CD相交于点M．若∠BAC＝70°，∠C＝30°，则∠BMD的大小为（ ）
A、50° B、65° C、70° D、80°8. 如图所示，已知AB∥DE，AB＝DE，BE＝CF，∠B＝32°，∠A＝78°，则∠F等于（ ）
A、55° B、65° C、60° D、70°9. 下列条件中，能利用“ ”判定△ ≌△A′B′C′的是 （ ）A、AB=A′B′，AC=A′C′，∠C=∠C′ B、AB=A′B′，∠A=∠A′，BC=B′C′ C、AC=A′C′，∠C=∠C′，BC=B′C′ D、AC=A′C′，∠A=∠A′，BC=B′C′10. 已知：AD是 的中线， ， ，则AD的取值范围是（ ）．A、 B、 C、 D、二、填空题
-
11. 如图，AD平分∠BAC，要使△ABD≌△ACD，可添加条件.（添加一个即可）
12. 如图，AB与CD交于点O， ， ， ， ，则 的度数为
13. 如图所示，F、C在线段BE上，且∠1＝∠2，BC＝EF.若要根据“SAS”使△ABC≌△DEF，还需要补充的条件是.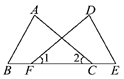
14. 如图所示，BD、AC相交于点O，若OA=OD，用“SAS”证明△AOB △DOC，还需.
15. 如图，小明与小红玩跷跷板游戏，如果跷跷板的支点O（即跷跷板的中点）至地面的距离是50cm，当小红从水平位置CD下降30cm时，这时小明离地面的高度是cm.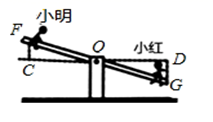
16. 如图，点B、E、C、F在一条直线上，AB∥DE，BE=CF，请添加一个条件 ， 使△ABC≌△DEF.
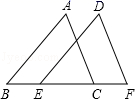17. 如图，点P、Q分别为等边△ABC的边AB、BC上的点，且AP＝BQ，若AQ与PC相交于点M，则∠AMC的度数为°.
18. 如图，四边形ABCD的对角线AC，BD相交于点O，△ABO≌△ADO．下列结论：①AC⊥BD；②CB＝CD；③DA＝DC；④△ABC≌△ADC，其中正确结论的序号是 ．
三、解答题
-
19. 如图所示，已知点B，E，C，F在一条直线上，AB=DF，AC=DE，∠A=∠D．求证：AC DE．
20. 如图，E、F是▱ABCD的对角线AC上的两点，AE＝CF.求证：EB＝DF（写出主要的证明依据）.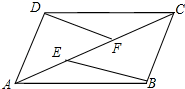
21. 如图， ， ， ，求证： .
22. 已知：如图，A、C、F、D在同一直线上， ＝ ， ， ＝ ，求证： △ABC ≌ △DEF
23. 如图，A、D、F、B在同一直线上，AD=BF，AE=BC，且AE∥BC．求证：△AEF≌△BCD．
24. 如图，C为BE上一点，点A，D分别在BE两侧，AB∥ED，AB＝CE，BC＝ED.求证：△ABC≌△CED.
25. 已知：如图，AB=AC ， AD=AE ， ∠1=∠2．求证：△ABD≌△ACE ．
