2021年苏科版数学八年级上册1.2 全等三角形 同步练习（提优版）
试卷更新日期：2021-08-31 类型：同步测试
一、单选题
-
1. 如图，△ABE≌△ACF，若AB=5，AE=2，则EC的长度是（ ）
A、2 B、3 C、4 D、52. 一个三角形的三边长分别为2，5，x，另一个三角形的三边长分别为y，2，6，若这两个三角形全等，则x+y=（ ）A、11 B、7 C、8 D、133. 如图，△ABN≌△ACM，AB=AC，BN=CM，∠B=50°，∠ANB=60°，则∠MAC的度数等于（ ）
A、120° B、70° C、60° D、50°．4. 如图， ， ， 于点E， 于点D， ， ，则 的长是（ ）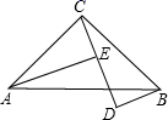
A、8 B、4 C、3 D、25. 如图，△ACF≌△BDE ， 点A、B、C、D在同一条直线上，下列结论中错误的是（ ）
A、AF∥BE B、∠ACF=∠DBE C、AB=CD D、CF∥DE6. 如图Δ ABC≌Δ A′B′C，则图中所有角中与∠BCB′相等的角(除∠BCB′ 外)共有（ ）.
A、1 个 B、2 个 C、3 个 D、4 个7. 如图，已知△ABC与△BDE全等，其中点D在边AB上，AB＞BC，BD=CA，DE∥AC，BC与DE交于点F，下列与AD+AC相等的是（ ）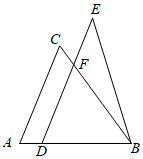
A、DE B、BE C、BF D、DF8. 如图，已知 ，下列结论：① ；② ；③ ；④ ；⑤ ；⑥ ；⑦ .其中正确的有（ ）
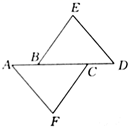A、 个 B、 个 C、 个 D、 个9. 如图，已知AB=CD且AB⊥CD，连接AD，分别过点C，B作CE⊥AD，BF⊥AD，垂足分别为E，F.若AD=10，CE=8，BF=6，则EF的长为（ ）
A、4 B、3.5 C、3 D、2.510. 已知：如图，在长方形ABCD中，AB=4，AD=6.延长BC到点E，使CE=2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC-CD-DA向终点A运动，设点P的运动时间为 秒，当 的值为_____秒时，△ABP和△DCE全等.
A、1 B、1或3 C、1或7 D、3或7二、填空题
-
11. 已知有两个三角形全等，若一个三角形三边的长分别为3、5、7，另一个三角形三边的长分别为3、3a﹣2b、a+2b ， 则a+b＝ ．12. 如图，△ADE≌△BCF，AD=8 cm，CD=6 cm，则BD的长为cm.
13. 如图，已知△ABC≌△A′BC′，AA′∥BC，∠ABC=70°，则∠CBC′= ．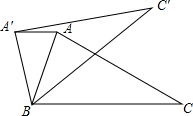
14. 如图为6个边长相等的正方形的组合图形，则 ．
15. 三个全等三角形按如图的形式摆放，则 度.
16. 如图，△ABC≌△ADE，BC的延长线交DE于点G.若∠B＝24°，∠CAB＝54°，∠DAC＝16°，则∠DGB＝.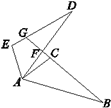
17. 如图，CA⊥AB，垂足为点A，AB=8厘米，AC=4厘米，射线BM⊥AB，垂足为点B，一动点E从A点出发以2厘米/秒的速度沿射线AN运动，点D为射线BM上一动点，随着E点运动而运动，且始终保持ED=CB，当点E离开点A后，运动 秒时，△DEB与△BCA全等.
18. 如图，锐角△ABC中，D、E分别是AB、AC边上的点，△ADC≌△ADC'，△AEB≌△AEB'，且C'D∥EB'∥BC，BE、CD交于点F，若∠BAC=a，∠BFC=b，则a与b之间的数量关系为.
三、解答题
-
19. 如图，△EFG≌△NMH，E，H，G，N在同一条直线上，EF和NM，FG和MH是对应边，若EH＝1.1cm，NH＝3.3cm．求线段HG的长．
20. 如图所示，△ABC≌△ADE，BC的延长线过点E，∠ACB=∠AED=105º，∠B=50º，∠CAD=10°，求出∠DEF的度数.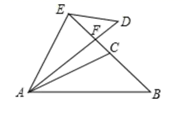
21. 如图，△ABC≌△ADE，且∠CAD=35°，∠B=∠D=20°，∠EAB=105°，求∠BFD和∠BED的度数.
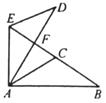22.如图，△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，求∠DFB和∠DGB的度数．
23.如图，△ABO≌△CDO，点B在CD上，AO∥CD，∠BOD=30°，求∠A的度数．
24. 如图，△ACE≌△DBF，AC＝6，BC＝4．
(1)、求证：AE∥DF；(2)、求AD的长度．25. 如图，点 、 、 、 在同一直线上， ．
(1)、求证： ．(2)、若 与 相交于点 ， ， ，求 的长．
