2021年苏科版数学八年级上册1.2 全等三角形 同步练习（基础版）
试卷更新日期：2021-08-31 类型：同步测试
一、单选题
-
1. 下列说法：（1）全等图形的形状相同，大小相等；（2）全等三角形的对应边相等；（3）全等图形的周长相等，面积相等；（4）面积相等的两个三角形全等.其中正确的是（ ）A、（1）（2）（4） B、（2）（3）（4） C、（1）（2）（3） D、（1）（2）（3）（4）2. 如图，△ABC≌△DEF，则下列结论正确的是（ ）
A、∠E＝60° B、∠F＝50° C、x＝18 D、x＝203. 如图，△ACB≌△A′C B′，∠ACB＝70°，∠ACB′＝100°，则∠BCA′度数是（ ）
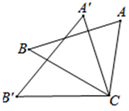A、40° B、35 C、30° D、45°4. 如图，若△ABC≌△DEF，BE＝22，BF＝5，则FC的长度是（ ）
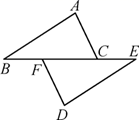A、10 B、12 C、8 D、165. 如图，△ABC≌△ADE，AB=AD，AC=AE，∠B=28°，∠E=95°，∠EAB=20°，则∠BAD等于（ ）
A、75° B、57° C、55° D、77°6. 如图，已知△ABC≌△ADE，若∠B＝40°，∠C＝75°，则∠EAD的度数为（ ）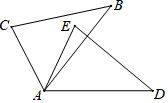
A、65° B、70° C、75° D、85°7. 如图，已知 ， ，则下列判断不正确的是（ ）
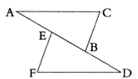A、 B、 C、 D、8. 已知△ABC≌△DEF，且△ABC中最大角的度数为100°，则△DEF中最大角的度数是（ ）A、90° B、100° C、120° D、150°9. 如图，平移△ABC得到△DEF ， 其中点A的对应点是点D ， 则下列结论中不成立的是（ ）
A、AD∥BE B、∠BAC＝∠DFE C、AC＝DF D、∠ABC＝∠DEF10. 如图，已知△ABC≌△CDA，则下列结论：①AB=CD，BC=DA.②∠BAC=∠DCA，∠ACB=∠CAD.③AB∥CD，BC∥DA.
其中正确的是（ ）
A、① B、② C、①② D、①②③二、填空题
-
11. 已知△ABC≌△A'B'C'，∠A＝60°，∠B＝40°，则∠C′＝.12. 若 ，且 的周长为12，若 .13. 一个三角形的三边为3、5、x，另一个三角形的三边为y、3、6，若这两个三角形全等，则x +y = ．14. 如图，已知△ABC≌△DEF ， 且BE=10cm，CF=4cm，则BC=
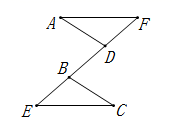
15. 如图，△ACE≌△DBF，如果∠E＝∠F，DA＝12，CB＝2，那么线段AB的长是 ．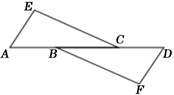
16. 如图， ，如果 ，那么 的长是.
17. 如图，若△ABC≌△ADE，且∠1＝35°，则∠2＝.
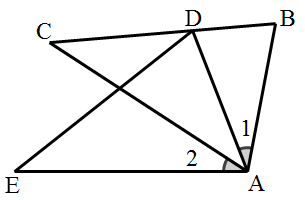18. 如图，△ACB≌△A′CB′，∠BCB′=30°，则∠ACA′的度数为°.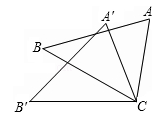
三、解答题
-
19. 如图，已知 ， ， ，求 的度数.
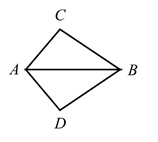20. 如图，已知△ABC≌△DEF，∠A＝85°，∠B＝60°，AB＝8，EH＝2.求∠F的度数与DH的长
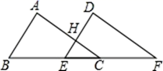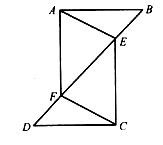
21. 如图，点B，F，C，E在同一条直线上，△ABC≌△DEF，点B与点E，点A与点D分别是对应点，AB＝6，BC＝11，BF＝3，∠ACB＝30°．求∠DFE的度数及DE，CE的长．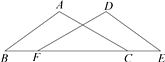
22. 如图，△ACF≌△DBE，∠E=∠F，若AD=11，BC=7，求线段AB的长.
23. 如图，已知△ABD≌△ACE．求证：BE=CD．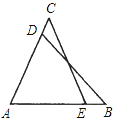
24. 如图，已知∆ABE≌∆ACD ， 求证：∠BAD=∠CAE ．
25. 如图，△ABO≌△CDO，点B在CD上，AO∥CD，∠BOD＝30°，求∠A的度数．
