高中数学人教A版(2019) 选修一 第二章 直线和圆的方程
试卷更新日期:2021-08-29 类型:单元试卷
一、单选题
-
1. 经过 , 两点的直线的方向向量为 ,则 的值是( )A、1 B、-1 C、2 D、-22. 已知直线 与直线 平行,则它们之间的距离是( )
A、 B、 C、8 D、23. 已知圆 与圆 没有公共点,则实数 的取值范围为( )A、 B、 C、 D、4. 已知 、 ,若点 在线段 上,则 的最小值为( )A、-1 B、3 C、7 D、85. 圆 内过点 的最短弦长为6,则实数 的值为( )A、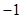 B、1
C、2
D、
B、1
C、2
D、 6. 过点 的直线 与 有两个不同的公共点,则直线 的倾斜角的范围是( )A、
6. 过点 的直线 与 有两个不同的公共点,则直线 的倾斜角的范围是( )A、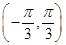 B、
B、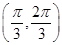 C、
C、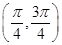 D、
D、 7. 两圆 与 的公切线有( )A、1条 B、2条 C、3条 D、4条8. 若直线 ( )过圆 的圆心,则 的最小值为( )A、16 B、20 C、12 D、8
7. 两圆 与 的公切线有( )A、1条 B、2条 C、3条 D、4条8. 若直线 ( )过圆 的圆心,则 的最小值为( )A、16 B、20 C、12 D、8二、多选题
-
9. 下列说法正确的是( )A、直线 必过定点(2,1) B、直线 在 轴上的截距为-2 C、直线 的倾斜角为120° D、若直线 沿 轴向左平移3个单位长度,再沿 轴向上平移2个单位长度后,回到原来的位置,则该直线 的斜率为10. 已知圆 和圆 的公共点为 , ,则( )A、 B、直线 的方程是 C、 D、11. 已知圆 : ,下列说法正确的是( )A、 的取值范围是 B、若 ,过 的直线与圆 相交所得弦长为 ,方程为 C、若 ,圆 与圆 相交 D、若 , , ,直线 恒过圆 的圆心,则 恒成立12. 在平面直角坐标系中, 为坐标原点,P为 轴上的动点,则下列说法正确的是( )A、 的最小值为2 B、若 ,则 的面积等于4 C、若 ,则 的最小值为5 D、若 ,且 与 的夹角 ,则
三、填空题
-
13. 过直线 和 的交点,且过点 的直线 的方程为 .14. 直线 与圆C: 相交于 、 两点,则弦长 的最小值为 .15. 经过两条直线 和 的交点,且垂直于直线 的直线的一般式方程为.16. 过点 作圆 的两条切线,切点为A,B,则直线 的一般式方程为.
四、解答题
-
17. 已知圆 ,直线 .(1)、若直线l平分圆C的周长,求实数k的值;(2)、若直线l与直线 的倾斜角互补,求圆C上的点到直线l的距离的最小值.18. 已知直线 过定点 .(1)、若直线 与直线 垂直,求直线 的方程;(2)、若直线 在两坐标轴上的截距相等,求直线 的方程.19. 圆 ,点 为直线 上一动点,过点 引圆 的两条切线,切点分别为 , .(1)、若点 的坐标为 ,求直线 、 的方程;(2)、求证:直线 恒过定点 ,并求出该定点 的坐标.20. 在下列所给的三个条件中任选一个,补充在下面的问题中,并加以解答.①与直线 垂直;②直线的一个方向向量为 ;③与直线 平行.已知直线 过点 ,______.(1)、求直线 的一般方程;(2)、若直线 与圆 相交于 、 ,求弦长 .