初中数学湘教版九年级上册第四章 锐角三角函数 单元测试
试卷更新日期:2021-08-29 类型:单元试卷
一、单选题
-
1. 如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )
 A、2sinα B、2tanα C、2cosα D、2. 的值等于( )A、 B、 C、 D、3. 在Rt△ABC中,∠C=90°,BC=8,AB=10,则sinA的值为( )A、 B、 C、 D、以上都不对4. 如图,小明利用一个锐角是 的三角板测量操场旗杆的高度,已知他与旗杆之间的水平距离 为 , 为 (即小明的眼睛与地面的距离),那么旗杆的高度是( )
A、2sinα B、2tanα C、2cosα D、2. 的值等于( )A、 B、 C、 D、3. 在Rt△ABC中,∠C=90°,BC=8,AB=10,则sinA的值为( )A、 B、 C、 D、以上都不对4. 如图,小明利用一个锐角是 的三角板测量操场旗杆的高度,已知他与旗杆之间的水平距离 为 , 为 (即小明的眼睛与地面的距离),那么旗杆的高度是( )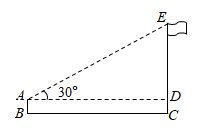 A、 B、 C、 D、5. 如图是某商场营业大厅自动扶梯的示意图.自动扶梯 的倾斜角为 ,大厅两层之间的距离 为6米,则自动扶梯 的长约为( )( ).
A、 B、 C、 D、5. 如图是某商场营业大厅自动扶梯的示意图.自动扶梯 的倾斜角为 ,大厅两层之间的距离 为6米,则自动扶梯 的长约为( )( ).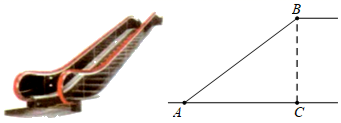 A、7.5米 B、8米 C、9米 D、10米6. 某限高曲臂道路闸口如图所示, 垂直地面 于点 , 与水平线 的夹角为 , ,若 米, 米,车辆的高度为 (单位:米),不考虑闸口与车辆的宽度.
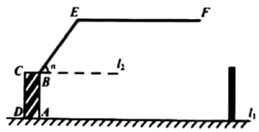
A、7.5米 B、8米 C、9米 D、10米6. 某限高曲臂道路闸口如图所示, 垂直地面 于点 , 与水平线 的夹角为 , ,若 米, 米,车辆的高度为 (单位:米),不考虑闸口与车辆的宽度.①当 时, 小于3.3米的车辆均可以通过该闸口;②当 时, 等于2.9米的车辆不可以通过该闸口;③当 时, 等于3.1米的车辆不可以通过该闸口.则上述说法正确的个数为( )
 A、0个 B、1个 C、2个 D、3个7. 如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为 ,坡顶D到BC的垂直距离 米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶A点的仰角为50°,则建筑物AB的高度约为(参考数据: ; ; )
A、0个 B、1个 C、2个 D、3个7. 如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为 ,坡顶D到BC的垂直距离 米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶A点的仰角为50°,则建筑物AB的高度约为(参考数据: ; ; )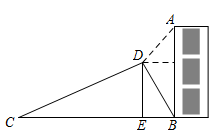 A、69.2米 B、73.1米 C、80.0米 D、85.7米8. 如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
A、69.2米 B、73.1米 C、80.0米 D、85.7米8. 如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )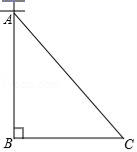 A、 B、 C、6cos50° D、9. 小明使用测角仪在甲楼底端A处测得熊猫C处的仰角为53°,在甲楼B处测得熊猫C处的仰角 已知AB=4.5米,则熊猫C处距离地面AD的高度为( )(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
A、 B、 C、6cos50° D、9. 小明使用测角仪在甲楼底端A处测得熊猫C处的仰角为53°,在甲楼B处测得熊猫C处的仰角 已知AB=4.5米,则熊猫C处距离地面AD的高度为( )(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33) A、13.6 B、18.1 C、17.3 D、16.810. 如图,在平面直角坐标系 中, , , , 是正方形 边上的线段,点 在其中某条线段上,若射线 与 轴正半轴的夹角为 ,且 ,则点 所在的线段可以是
A、13.6 B、18.1 C、17.3 D、16.810. 如图,在平面直角坐标系 中, , , , 是正方形 边上的线段,点 在其中某条线段上,若射线 与 轴正半轴的夹角为 ,且 ,则点 所在的线段可以是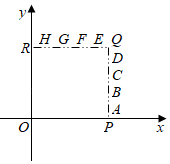 A、 和 B、 和 C、 和 D、 和
A、 和 B、 和 C、 和 D、 和二、填空题
-
11. sin30°=12. 若sin(x﹣30°)= ,则x=.13. 某市跨江大桥即将竣工,某学生做了一个平面示意图(如图),点A到桥的距离是40米,测得∠A=83°,则大桥BC的长度是 米.(结果精确到1米)(参考数据:sin83°≈0.99,cos83°≈0.12,tan83°≈8.14)
 14. 数学活动小组为测量山顶电视塔的高度,在塔的椭圆平台遥控无人机.当无人机飞到点P处时,与平台中心O点的水平距离为15米,测得塔顶A点的仰角为30°,塔底B点的俯角为60°,则电视塔的高度为米.
14. 数学活动小组为测量山顶电视塔的高度,在塔的椭圆平台遥控无人机.当无人机飞到点P处时,与平台中心O点的水平距离为15米,测得塔顶A点的仰角为30°,塔底B点的俯角为60°,则电视塔的高度为米.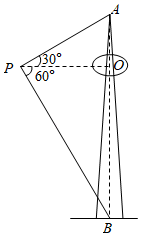 15. 数学兴趣小组利用无人机测量学校旗杆高度,已知无人机的飞行高度为40米,当无人机与旗杆的水平距离是45米时,观测旗杆顶部的俯角为30°,则旗杆的高度约为米.(结果精确到1米,参考数据: , )
15. 数学兴趣小组利用无人机测量学校旗杆高度,已知无人机的飞行高度为40米,当无人机与旗杆的水平距离是45米时,观测旗杆顶部的俯角为30°,则旗杆的高度约为米.(结果精确到1米,参考数据: , ) 16. BD为等腰△ABC的腰AC上的高,BD=1,tan∠ABD= ,则CD的长为.
16. BD为等腰△ABC的腰AC上的高,BD=1,tan∠ABD= ,则CD的长为.三、计算题
-
17. 计算: .18. 计算:19. 计算:(1)、3tan230°+ tan60°-2sin245°;(2)、(2019-π)0-4cos30°+ +|1- |.
四、解答题
-
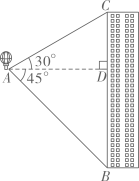
20. 热气球的探测器显示,从热气球A处看大楼BC顶部C的仰角为30°,看大楼底部B的俯角为45°,热气球与该楼的水平距离AD为60米,求大楼BC的高度.(结果精确到1米,参考数据: )
 21. 有诗云:东山雨霁画屏开,风卷松声入耳来.一座楼阁镇四方,团结一心建家乡.1987年为庆祝湘西自治州成立三十周年,湘西州政府在花果山公园内修建了一座三层楼高的“一心阁”民族团结楼阁.芙蓉学校数学实践活动小组为测量“一心阁” 的高度,在楼前的平地上A处,观测到楼顶 处的仰角为30°,在平地上 处观测到楼顶 处的仰角为 ,并测得A、 两处相距 ,求“一心阁” 的高度.(结果保留小数点后一位,参考数据: , )
21. 有诗云:东山雨霁画屏开,风卷松声入耳来.一座楼阁镇四方,团结一心建家乡.1987年为庆祝湘西自治州成立三十周年,湘西州政府在花果山公园内修建了一座三层楼高的“一心阁”民族团结楼阁.芙蓉学校数学实践活动小组为测量“一心阁” 的高度,在楼前的平地上A处,观测到楼顶 处的仰角为30°,在平地上 处观测到楼顶 处的仰角为 ,并测得A、 两处相距 ,求“一心阁” 的高度.(结果保留小数点后一位,参考数据: , ) 22. 某区域平面示意图如图所示,点D在河的右侧,红军路AB与某桥BC互相垂直.某校“数学兴趣小组”在“研学旅行”活动中,在C处测得点D位于西北方向,又在A处测得点D位于南偏东65°方向,另测得 , ,求出点D到AB的距离.(参考数据 , , )
22. 某区域平面示意图如图所示,点D在河的右侧,红军路AB与某桥BC互相垂直.某校“数学兴趣小组”在“研学旅行”活动中,在C处测得点D位于西北方向,又在A处测得点D位于南偏东65°方向,另测得 , ,求出点D到AB的距离.(参考数据 , , )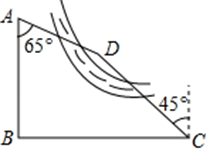
五、综合题
-
23. 如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα= = ,根据上述角的余切定义,解下列问题:
 (1)、ctan30°=;(2)、如图,已知tanA= ,其中∠A为锐角,试求ctanA的值.24. 如图,两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍船只停在C处海域,AB=60( +1)海里,在B处测得C在北偏东45°反向上,A处测得C在北偏西30°方向上,在海岸线AB上有一灯塔D,测得AD=100海里.
(1)、ctan30°=;(2)、如图,已知tanA= ,其中∠A为锐角,试求ctanA的值.24. 如图,两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍船只停在C处海域,AB=60( +1)海里,在B处测得C在北偏东45°反向上,A处测得C在北偏西30°方向上,在海岸线AB上有一灯塔D,测得AD=100海里. (1)、分别求出AC,BC(结果保留根号).
(1)、分别求出AC,BC(结果保留根号).
(2)、已知在灯塔D周围80海里范围内有暗礁群,在A处海监穿沿AC前往C处盘查,途中有无触礁的危险?请说明理由.25. 货车长方体货厢的净高BC为2.5 m,底部B离地面的高度BD为1.2 m.现欲将高为2 m的正方体货物装进货厢,工人师傅搭了坡度为i=1∶3的坡面AB. (1)、若货物从如图所示的位置升高0.5 m,则水平移动了多少?(2)、由于货物较重但分布均匀,工人师傅试图将货物沿坡面AB推到适当位置后,再轻松平放进货厢.请问能否达到目的?为什么?
(1)、若货物从如图所示的位置升高0.5 m,则水平移动了多少?(2)、由于货物较重但分布均匀,工人师傅试图将货物沿坡面AB推到适当位置后,再轻松平放进货厢.请问能否达到目的?为什么?