初中数学湘教版九年级上册4.2正切 同步练习
试卷更新日期:2021-08-29 类型:同步测试
一、单选题
-
1. 的值等于( )A、 B、 C、1 D、22. 在 中, , , , , ,则BC的长为( )A、6 B、 C、8 D、3. 在Rt△ABC中,∠C=90°,a=5,b=12,则tanB的值为( )A、 B、 C、 D、4. 如图,A,B,C是3×1的正方形网格中的三个格点,则 tan∠ABC的值为( )
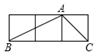 A、 B、 C、 D、5. 若锐角α满足cosα< 且tanα< ,则α的范围是( )A、30°<α<45° B、45°<α<60° C、60°<α<90° D、30°<α<60°6. 在Rt△ABC中,∠C = 90°,∠A、∠B、∠C所对的边分别为a、b、c , 下列等式中成立的是( )A、 B、 C、 D、
A、 B、 C、 D、5. 若锐角α满足cosα< 且tanα< ,则α的范围是( )A、30°<α<45° B、45°<α<60° C、60°<α<90° D、30°<α<60°6. 在Rt△ABC中,∠C = 90°,∠A、∠B、∠C所对的边分别为a、b、c , 下列等式中成立的是( )A、 B、 C、 D、二、填空题
-
7. tan60°的值等于 .8. 若 ,则锐角 的度数是.9. 如图, 的顶点都是正方形网格中的格点,则 .
 10. 已知 是锐角,且 ,那么 .11. 在△ABC中,∠C=90°,tanA= ,则cosB=。12. 在Rt△ABC中,∠C=90°,AC=3,BC=4,则tanA的值为.13. 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD⊥AB,垂足为D,则tan∠BCD的值是.
10. 已知 是锐角,且 ,那么 .11. 在△ABC中,∠C=90°,tanA= ,则cosB=。12. 在Rt△ABC中,∠C=90°,AC=3,BC=4,则tanA的值为.13. 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD⊥AB,垂足为D,则tan∠BCD的值是.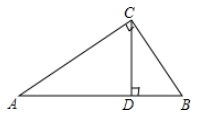 14. 规定sin(α﹣β)=sinα•cosβ﹣cosα•sinβ,则sin15°= .
14. 规定sin(α﹣β)=sinα•cosβ﹣cosα•sinβ,则sin15°= .三、计算题
-
15. 计算: .16. 求满足下列条件的锐角x:(1)、(2)、17. 计算: .
四、解答题
-
18. 计算: .19. 如图所示,我县某中学课外活动小组的同学利用所学知识去测量怀安河的宽度,小明同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处20米远的B处测得∠CBA=30°,请你根据这些数据算出河宽.(结果保留根号)
 20. 步行是全世界公认的有效、科学的健身方法.为了方便市民步行健身,某区园林部门决定将某公园里的一段斜坡 改造成 .已知原坡角 ,改造后的斜坡 的坡度为 , 米,求原斜坡 的长.(精确到0.1米,参考数据: )
20. 步行是全世界公认的有效、科学的健身方法.为了方便市民步行健身,某区园林部门决定将某公园里的一段斜坡 改造成 .已知原坡角 ,改造后的斜坡 的坡度为 , 米,求原斜坡 的长.(精确到0.1米,参考数据: )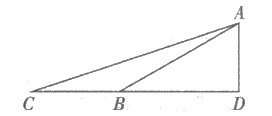
五、作图题
-
21. 图①、图②均是6×6的正方形网格,每个小正方形的顶点称为格点.线段AB的端点均在格点上,按下列要求画出图形.
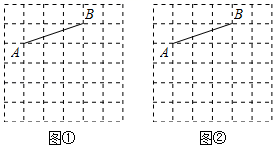
( 1 )在图①中找到两个格点C,使∠BAC是锐角,且tan∠BAC= ;
( 2 )在图②中找到两个格点D,使∠ADB是锐角,且tan∠ADB=1.
22. 图①、图②均是6×6的正方形网格,每个小正方形的顶点称为格点.线段AB的端点均在格点上,按下列要求画出图形. (1)、在图①中找到一个格点C , 使∠ABC是锐角,且tan∠ABC= ,并画出△ABC .(2)、在图②中找到一个格点D , 使∠ADB是锐角,且tan∠ADB=1,并画出△ABD .
(1)、在图①中找到一个格点C , 使∠ABC是锐角,且tan∠ABC= ,并画出△ABC .(2)、在图②中找到一个格点D , 使∠ADB是锐角,且tan∠ADB=1,并画出△ABD .六、综合题
-
23. 如图,在Rt△ABC中,∠C=90°,D是BC边上一点,AC=2,CD=1,设∠CAD=α.
 (1)、求sinα、cosα、tanα的值;(2)、若∠B=∠CAD,求BD的长.24. 在“停课不停学”期间,小明用电脑在线上课,图1是他的电脑液晶显示器的侧面图,显示屏AB可以绕点O旋转一定的角度.研究表明:当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个18°的俯角(即望向屏幕中心P的视线EP与水平线EA的夹角∠AEP)时,对保护眼睛比较好,而且显示屏顶端A与底座C的连线AC与水平线CD垂直时(如图2)时,观看屏幕最舒适。此时测得∠BCD=30°,∠APE=90°,液晶显示屏的宽AB为32cm。
(1)、求sinα、cosα、tanα的值;(2)、若∠B=∠CAD,求BD的长.24. 在“停课不停学”期间,小明用电脑在线上课,图1是他的电脑液晶显示器的侧面图,显示屏AB可以绕点O旋转一定的角度.研究表明:当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个18°的俯角(即望向屏幕中心P的视线EP与水平线EA的夹角∠AEP)时,对保护眼睛比较好,而且显示屏顶端A与底座C的连线AC与水平线CD垂直时(如图2)时,观看屏幕最舒适。此时测得∠BCD=30°,∠APE=90°,液晶显示屏的宽AB为32cm。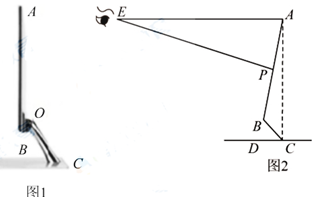 (1)、求眼睛E与显示屏顶端A的水平距离AE.(结果精确到1cm)(2)、求显示屏顶端A与底座C的距离AC。(结果精确到1cm)
(1)、求眼睛E与显示屏顶端A的水平距离AE.(结果精确到1cm)(2)、求显示屏顶端A与底座C的距离AC。(结果精确到1cm)(参考数据:sin18°≈0.3,cos18°≈0.9,tan18°≈0.3, ≈1.4, ≈1.7)
25.(1)、完成下列表格,并回答下列问题,锐角
(2)、当锐角 逐渐增大时, 的值逐渐 , 的值逐渐 , 的值逐渐 .(3)、 , ;(4)、 ;(5)、 ;(6)、若 ,则锐角 .