湘教版数学九年级上册同步训练《2.3 一元二次方程根的判别式》

试卷更新日期：2021-08-28 类型：同步测试

进入出卷网下载

一、单选题

1. 若方程 $x^{2} - 2 x + m = 0$ 没有实数根，则 $m$ 的值可以是（）

A、-1 B、 $0$ C、1 D、 $\sqrt{3}$

查看试题解析
2. 对于实数 $a ， b$ 定义运算“☆”如下： $a ☆ b = a b^{2} - a b$ ，例如 $3 ☆ 2 = 3 \times 2^{2} - 3 \times 2 = 6$ ，则方程 $1 ☆ x = 2$ 的根的情况为（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
3. 在平面直角坐标系中，若直线 $y = - x + m$ 不经过第一象限，则关于 $x$ 的方程 $m x^{2} + x + 1 = 0$ 的实数根的个数为（）

A、0个 B、1个 C、2个 D、1或2个

查看试题解析
4. 关于 $x$ 的一元二次方程 $(a + 2) x^{2} - 3 x + 1 = 0$ 有实数根，则 $a$ 的取值范围是（）

A、 $a \leq \frac{1}{4}$ 且 $a \neq - 2$ B、 $a \leq \frac{1}{4}$ C、 $a < \frac{1}{4}$ 且 $a \neq - 2$ D、 $a < \frac{1}{4}$

查看试题解析
5. 已知关于x的一元二次方程 $x^{2} - m n x + m + n = 0$ ，其中m ， n在数轴上的对应点如图所示，则这个方程的根的情况是（）

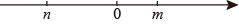A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
6. 如果关于x的一元二次方程 $k x^{2} - 3 x + 1 = 0$ 有两个实数根，那么 $k$ 的取值范围是（）

A、 $k ⩾ \frac{9}{4}$ B、 $k ⩾ - \frac{9}{4}$ 且 $k \neq 0$ C、 $k ⩽ \frac{9}{4}$ 且 $k \neq 0$ D、 $k ⩽ - \frac{9}{4}$

查看试题解析
7. 定义新运算“※”：对于实数m，n，p，q，有 $[m ， p] ※ [q ， n] = m n + p q$ ，其中等式右边是通常的加法和乘法运算，如： $[2 ， 3] ※ [4 ， 5] = 2 \times 5 + 3 \times 4 = 22$ .若关于x的方程 $[x^{2} + 1 ， x] ※ [5 - 2 k ， k] = 0$ 有两个实数根，则k的取值范围是（）

A、 $k < \frac{5}{4}$ 且 $k \neq 0$ B、 $k \leq \frac{5}{4}$ C、 $k \leq \frac{5}{4}$ 且 $k \neq 0$ D、 $k \geq \frac{5}{4}$

查看试题解析
8. 关于x的一元二次方程 $x^{2} - (k - 3) x - k + 1 = 0$ 的根的情况，下列说法正确的是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
9. 函数 $y = k x + b$ 的图象如图所示，则关于x的一元二次方程 $x^{2} + b x + k - 1 = 0$ 的根的情况是（）

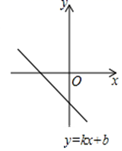A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法确定

查看试题解析
10. 抛物线 $y = a x^{2} + b x + c$ （a，b，c为常数）开口向下且过点 $A (1 ， 0)$ ， $B (m ， 0)$ （ $- 2 < m < - 1$ ），下列结论：① $2 b + c > 0$ ；② $2 a + c < 0$ ；③ $a (m + 1) - b + c > 0$ ；④若方程 $a (x - m) (x - 1) - 1 = 0$ 有两个不相等的实数根，则 $4 a c - b^{2} < 4 a$ .其中正确结论的个数是（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

11. 若关于 $x$ 的一元二次方程 $x^{2} + 3 x + c = 0$ 有两个相等的实数根，则 $c$ 的值为．

查看试题解析
12. 一元二次方程 $x^{2} - 4 x + m = 0$ 有两个相等的实数根，点 $A (x_{1} ， y_{1})$ 、 $B (x_{2} ， y_{2})$ 是反比例函数 $y = \frac{m}{x}$ 上的两个点，若 $x_{1} < x_{2} < 0$ ，则 $y_{1}$ $y_{2}$ （填“＜”或“＞”或“＝”）．

查看试题解析
13. 若关于x的一元二次方程 $x^{2} - 2 x + m = 0$ 有两个不相等的实数根，则m的值可以是.（写出一个即可）

查看试题解析
14. 若关于x的一元二次方程 ${(x + 2)}^{2} = n$ 有实数根，则n的取值范围是.

查看试题解析
15. 若关于x的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 各项系数满足 $a + b + c = 0$ ，则此方程的根的情况：①必有两个不相等的实数根；②当 $a = c$ 时，有两个相等的实数根；③当a ， c同号时，方程有两个正的实数根；④当a ， b同号时，方程有两个异号实数根．其中结论正确的个数是个．

查看试题解析
16. 关于x的方程 $x^{2} - 2 x + m = p^{2}$ ，无论实数p取何值，该方程总有两个不相等的实数根，则实数m的取值范围为.

查看试题解析

三、解答题

17. 已知关于x的一元二次方程（m﹣1）x²+2mx+m﹣3＝0，求：当方程有两个不相等的实数根时m的取值范围.

查看试题解析
18. 已知a，b，c是△ABC的三边长，且方程 $(a^{2} + b^{2}) x^{2} - 2 c x + 1 ＝ 0$ 有两个相等的实数根.请你判断△ABC的形状.

查看试题解析
19. 已知关于 $x$ 的方程 $x^{2} - (2 k - 1) x - 2 k = 0$ ，求证：不论 $k$ 取何值，这个方程都有两个实数根．

查看试题解析
20. 已知：A＝（m+1）（m﹣1）﹣（m+2）（m﹣3）

(1)、化简A；

(2)、若关于x的一元二次方程x²+（m+2）x+ $\frac{1}{4}$ m²＝0有两个相等的实数根，求A的值．

查看试题解析
21. 关于x的一元二次方程（m﹣1）x²﹣x﹣2＝0

(1)、若x＝﹣1是方程的一个根，求m的值及另一个根．

(2)、当m为何值时方程有两个不同的实数根．

查看试题解析
22. 关于x的一元二次方程 $m x^{2} － x + 1 ＝ 0$ 有两个不相等的实数根．

(1)、求m的取值范围；

(2)、当m为最大的整数时，解这个一元二次方程．

查看试题解析