初中数学湘教版九年级上册第三章 图形的相似 单元测试
试卷更新日期:2021-08-28 类型:单元试卷
一、单选题
-
1. 如图,平面直角坐标系中,已知 顶点 ,以原点 为位似中心,将 缩小后得到 ,若 的面积为 ,则 的面积为( )
 A、 B、 C、 D、2. 如图,在△ABC中,点D,E分别在边AB,AC上,且 ,则 的值为( )
A、 B、 C、 D、2. 如图,在△ABC中,点D,E分别在边AB,AC上,且 ,则 的值为( )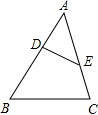 A、 B、1:2 C、1:3 D、1:43. 如图,已知△ABC,则下列4个三角形中,与△ABC相似的是( )
A、 B、1:2 C、1:3 D、1:43. 如图,已知△ABC,则下列4个三角形中,与△ABC相似的是( ) A、
A、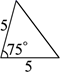 B、
B、 C、
C、 D、
D、 4. 如图, 平行 平行 ,下列比例式中正确的是( )
4. 如图, 平行 平行 ,下列比例式中正确的是( ) A、 B、 C、 D、5. 如图,在平面直角坐标系中,将 以原点O为位似中心放大后得到 ,若 , ,则 与 的相似比是( )
A、 B、 C、 D、5. 如图,在平面直角坐标系中,将 以原点O为位似中心放大后得到 ,若 , ,则 与 的相似比是( )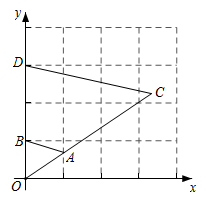 A、2:1 B、1:2 C、3:1 D、1:36. 如图,在平面直角坐标系中,已知点 , , ,以某点为位似中心,作出与 的位似比为 的位似 ,则位似中心的坐标和 的值分别为( )
A、2:1 B、1:2 C、3:1 D、1:36. 如图,在平面直角坐标系中,已知点 , , ,以某点为位似中心,作出与 的位似比为 的位似 ,则位似中心的坐标和 的值分别为( )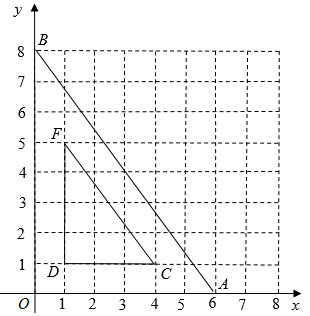 A、(0,0), B、(1,1),2 C、(2,2), D、(1,1),7. 如图, 、 交于 点, ,则下列结论一定正确的是( )
A、(0,0), B、(1,1),2 C、(2,2), D、(1,1),7. 如图, 、 交于 点, ,则下列结论一定正确的是( ) A、 B、 C、 D、8. 小刚身高 ,测得他站立在阳光下的影子长为 ,紧接着他把手臂竖直举起,测得影子长为 ,那么小刚举起的手臂超出头顶( )A、 B、 C、 D、9. 如图,在 ABC中,点D在AB边上,点E在BC边上,过点D作DG BC , 交AC于点G , 过点E作EH AB , 交AC于点H , DG的延长线与EH的延长线交于点F , 则下列式子一定正确的是( )
A、 B、 C、 D、8. 小刚身高 ,测得他站立在阳光下的影子长为 ,紧接着他把手臂竖直举起,测得影子长为 ,那么小刚举起的手臂超出头顶( )A、 B、 C、 D、9. 如图,在 ABC中,点D在AB边上,点E在BC边上,过点D作DG BC , 交AC于点G , 过点E作EH AB , 交AC于点H , DG的延长线与EH的延长线交于点F , 则下列式子一定正确的是( )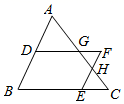 A、 B、 C、 D、10. 如图,在Rt△ABC中,∠ACB=90°,分别以其三边为边向外作正方形,延长EA交BG于点M,连接IM交AB于点N,若M是BG的中点,则 的值为( )
A、 B、 C、 D、10. 如图,在Rt△ABC中,∠ACB=90°,分别以其三边为边向外作正方形,延长EA交BG于点M,连接IM交AB于点N,若M是BG的中点,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 2021年3月20日起,我国陆续公布了三星堆遗址考古最新发掘成果.地球表面纬度范围是0~90°,对其进行黄金分割,黄金分割点间地区特别适合人类生活,产生了包括三星堆在内的世界古文明,也囊括了大多发达国家.那么黄金地带纬度的范围是.(黄金比为0.618)
 12. 已知△ABC的三边分别是5,6,7,则与它相似△ 的最短边为10,则△ 的周长是13. 如图,直线 ,分别交直线m,n于点A,B,C,D,E,F,若 , , ,则EF的长为.
12. 已知△ABC的三边分别是5,6,7,则与它相似△ 的最短边为10,则△ 的周长是13. 如图,直线 ,分别交直线m,n于点A,B,C,D,E,F,若 , , ,则EF的长为. 14. 如图,当∠AED=时,△ADE与△ABC相似.
14. 如图,当∠AED=时,△ADE与△ABC相似.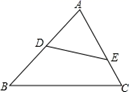 15. 《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆 ,从木杆的顶端B观察井水水岸D , 视线 与井口的直径 交于点E , 如果测得 米, 米, 米,那么 为米.
15. 《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆 ,从木杆的顶端B观察井水水岸D , 视线 与井口的直径 交于点E , 如果测得 米, 米, 米,那么 为米.
 16. 如图,在△ABC中,AB=4,BC=5,点D、E分别在BC、AC上,CD=2BD,CF=2AF,BE交AD于点F,则△AFE面积的最大值是.
16. 如图,在△ABC中,AB=4,BC=5,点D、E分别在BC、AC上,CD=2BD,CF=2AF,BE交AD于点F,则△AFE面积的最大值是.
三、计算题
-
17. 如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,AB=5,求 的值.
 18. 如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,求DF的长度.
18. 如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,求DF的长度.
四、解答题
-
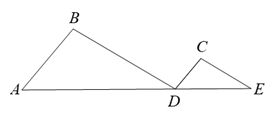
19. 如图,已知 ∥ , .求证: .
 20. 如图, ,直线 , 与这三条平行线分别交于点 , , 和点 , , ,已知 , , ,则 的长为?
20. 如图, ,直线 , 与这三条平行线分别交于点 , , 和点 , , ,已知 , , ,则 的长为?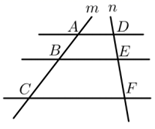
五、作图题
-
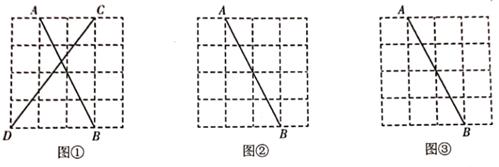
21. 图、图②、图③均是4×4的正方形网格,每个小正方形的顶点称为格点,线段AB的端点均在格点上.在图②、图③中仿照图①,只用无刻度的直尺,各画出一条线段CD,将线段AB分为23两部分。
要求:所画线段CD的位置不同,点C、D均在格点上。
 22. 如图,图中的小方格都是边长为1的正方形, △ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
22. 如图,图中的小方格都是边长为1的正方形, △ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上. (1)、画出位似中心点O;(2)、求出△ABC与△A′B′C′的位似比;(3)、以点O为位似中心,再画一个△A1B1C1 , 使它与△ABC的位似比等于1.5.
(1)、画出位似中心点O;(2)、求出△ABC与△A′B′C′的位似比;(3)、以点O为位似中心,再画一个△A1B1C1 , 使它与△ABC的位似比等于1.5.六、综合题
-
23. 如图,强强同学为了测量学校一棵笔直的大树OE的高度,先在操场上点A处放一面平面镜,从点A处后退1m到点B处,恰好在平面镜中看到树的顶部E点的像;再将平面镜向后移动4m(即AC=4m)放在C处,从点C处向后退1.5m到点D处,恰好再次在平面镜中看到大树的顶部E点的像,测得强强的眼睛距地面的高度FB、GD为1.5m,已知点O,A,B,C,D在同一水平线上,且GD⊥OD,FB⊥OD,EO⊥OD.求大树OE的高度.(平面镜的大小忽略不计)


