北师版数学九年级上册《第二章一元二次方程》检测卷B卷

试卷更新日期：2021-08-28 类型：单元试卷

进入出卷网下载

一、单选题

1. 已知关于x的一元二次方程x²+5x﹣m＝0的一个根是2，则另一个根是（）

A、﹣7 B、7 C、3 D、﹣3

查看试题解析
2. 已知关于x的一元二次方程 $a x^{2} - 4 x - 1 = 0$ 有两个不相等的实数根，则a的取值范围是（）

A、 $a \geq - 4$ B、 $a > - 4$ C、 $a \geq - 4$ 且 $a \neq 0$ D、 $a > - 4$ 且 $a \neq 0$

查看试题解析
3. 根据表格中的信息，估计一元二次方程 $a x^{2} + b x + c = 5$ （ $a$ 、 $b$ 、 $c$ 为常数， $a \neq 0$ ）的一个解 $x$ 的范围为（）

x

0

1

2

3

4

ax²+bx+c

-14.5

-11.5

-6.5

0.5

9.5

A、 $0 < x < 1$ B、 $1 < x < 2$ C、 $2 < x < 3$ D、 $3 < x < 4$

查看试题解析
4. 一元二次方程 $x^{2} - 8 x - 2 = 0$ ，配方后可形为（）

A、 ${(x - 4)}^{2} = 18$ B、 ${(x - 4)}^{2} = 14$ C、 ${(x - 8)}^{2} = 64$ D、 ${(x - 4)}^{2} = 1$

查看试题解析
5. 已知关于x的一元二次方程： $x^{2} - 2 x + m = 0$ 有两个不相等的实数根 $x_{1}$ ， $x_{2}$ ，则（）

A、 $x_{1} + x_{2} < 0$ B、 $x_{1} x_{2} < 0$ C、 $x_{1} x_{2} > - 1$ D、 $x_{1} x_{2} < 1$

查看试题解析
6. 已知方程 $x^{2} - 2021 x + 1 = 0$ 的两根分别为 $x_{1}$ ， $x_{2}$ ，则 $x_{1}^{2} - \frac{2021}{x_{2}}$ 的值为（）

A、1 B、-1 C、2021 D、-2021

查看试题解析
7. 关于x的方程 $x^{2} + 2 (m - 1) x + m^{2} - m = 0$ 有两个实数根 $α$ ， $β$ ，且 $α^{2} + β^{2} = 12$ ，那么m的值为（）

A、-1 B、-4 C、-4或1 D、-1或4

查看试题解析
8. 有一个人患了流行性感冒，经过两轮传染后共有144人患了流行性感冒，则每轮传染中平均一个人传染的人数是（）

A、14 B、11 C、10 D、9

查看试题解析
9. 已知二次函数 $y = (a - 2) x^{2} - (a + 2) a + 1$ ，当x取互为相反数的任意两个实数值时，对应的函数值y总相等，则关于x的一元二次方程 $(a - 2) x^{2} - (a + 2) x + 1 = 0$ 的两根之积为（）

A、0 B、 $- 1$ C、 $- \frac{1}{2}$ D、 $- \frac{1}{4}$

查看试题解析
10. 关于x的方程 $(x - 1) (x + 2) = ρ^{2}$ （ $ρ$ 为常数）根的情况下，下列结论中正确的是（）

A、两个正根 B、两个负根 C、一个正根，一个负根 D、无实数根

查看试题解析
11. 若 $x_{1} + x_{2} = 3$ ， $x_{1}^{2} + x_{2}^{2} = 5$ ，则以 $x_{1}$ ， $x_{2}$ 为根的一元二次方程是（）

A、 $x^{2} - 3 x + 2 = 0$ B、 $x^{2} + 3 x - 2 = 0$ C、 $x^{2} + 3 x + 2 = 0$ D、 $x^{2} - 3 x - 2 = 0$

查看试题解析
12. 如图，学校课外生物小组的试验园地的形状是长35米、宽20米的矩形．为便于管理，要在中间开辟一横两纵共三条等宽的小道，使种植面积为600平方米，则小道的宽为多少米？若设小道的宽为 $x$ 米，则根据题意，列方程为（）

A、 $35 \times 20 - 35 x - 20 x + 2 x^{2} = 600$ B、 $35 \times 20 - 35 x - 2 \times 20 x = 600$ C、 $(35 - 2 x) (20 - x) = 600$ D、 $(35 - x) (20 - 2 x) = 600$

查看试题解析

二、填空题

13. 关于x的方程x²﹣（3k+1）x+2k²+2k＝0，若等腰三角形△ABC一边长为a＝6，另两边长b，c为方程两个根，则△ABC的周长为.

查看试题解析
14. 已知实数a、b满足 $\sqrt{a - 2} + | b + 3 | = 0$ ，若关于x的一元二次方程 $x^{2} - a x + b = 0$ 的两个实数根分别为 $x_{1}$ 、 $x_{2}$ ，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}} =$ .

查看试题解析
15. 设 $x_{1} ， x_{2}$ 是关于x的方程 $x^{2} - 3 x + k = 0$ 的两个根，且 $x_{1} = 2 x_{2}$ ，则 $k =$ .

查看试题解析
16. 已知关于 $x$ 的方程 $x^{2} - (k + 4) x + 4 k = 0$ （ $k \neq 0$ ）的两实数根为 $x_{1}$ ， $x_{2}$ ，若 $\frac{2}{x_{1}} + \frac{2}{x_{2}} = 3$ ，则 $k =$ .

查看试题解析
17. 在设计人体雕像时，使雕像的上部（腰以上）与下部（腰以下）的高度比，等于下部与全部（全身）的高度比，可以增加视觉美感按此比例，如果雕像的高为3m，那么它的下部应设计为多高？设它的下部设计高度为xm，根据题意，可列方程为．

查看试题解析

18. 数学活动课上，小云和小王在讨论张老师出示的一道代数式求值问题：

已知实数a，b同时满足a²+2a＝b+2，b²+2b＝a+2，求代数式 $\frac{b}{a} + \frac{a}{b}$ 的值．

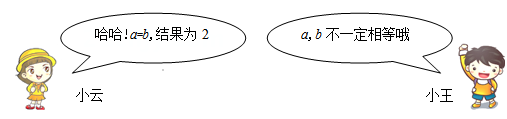
结合他们的对话，请解答下列问题：

(1)、当a＝b时，a的值是．

(2)、当a≠b时，代数式

\frac{b}{a} + \frac{a}{b}

的值是．

查看试题解析

三、解答题

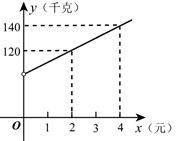
19. 解下列方程：

(1)、x²﹣6x﹣3＝0；

(2)、3x（x﹣1）＝2（1﹣x）.

查看试题解析
20. 按要求解下列方程：

(1)、用配方法解：x²﹣4x+1＝0.

(2)、用公式法解： $x^{2} - \sqrt{2} x - \frac{1}{4} = 0$ .

查看试题解析
21. 已知关于x的一元二次方程 $x^{2} - 4 x - 2 m + 5 = 0$ 有两个不相等的实数根.

(1)、求实数m的取值范围；

(2)、若该方程的两个根都是符号相同的整数，求整数m的值.

查看试题解析
22. 已知 $x_{1}$ ， $x_{2}$ 是一元二次方程 $x^{2} - 2 x + k + 2 = 0$ 的两个实数根．

(1)、求k的取值范围；

(2)、是否存在实数k，使得等式 $\frac{1}{x_{1}} + \frac{1}{x_{2}} = k - 2$ 成立？如果存在，请求出k的值，如果不存在，请说明理由．

查看试题解析
23. 一商店销售某种商品，平均每天可售出20件，每件盈利40元.为了扩大销售、增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件.

(1)、若降价3元，则平均每天销售数量为件；

(2)、当每件商品降价多少元时，该商店每天销售利润为1200元？

查看试题解析
24. 安顺市某商贸公司以每千克40元的价格购进一种干果，计划以每千克60元的价格销售，为了让顾客得到更大的实惠，现决定降价销售，已知这种干果销售量y（千元）与每千元降价x（元）（0<x<20）之间满足一次函数关系，其图象如图所示：

(1)、求y与x之间的函数关系式；

(2)、商贸公司要想获利2090元，则这种干果每千克应降价多少元？

查看试题解析
25. 阅读理解：
材料一：若三个非零实数x ， y ， z满足：只要其中一个数的倒数等于另外两个数的倒数的和，则称这三个实教x ， y ， z构成“和谐三数组”.

材料二：若关于x的一元二次方程ax²+bx +c= 0(a≠0)的两根分别为 $x_{1}$ ， $x_{2}$ ，则有 $x_{1} + x_{2} = - \frac{b}{a}$ ， $x_{1} \cdot x_{2} = \frac{c}{a}$ ．

问题解决：

(1)、请你写出三个能构成“和谐三数组”的实数；

(2)、若 $x_{1}$ ， $x_{2}$ 是关于x的方程ax²+bx +c= 0 (a ， b ， c均不为0)的两根， $x_{3}$ 是关于x的方程bx+c=0(b ， c均不为0)的解．求证：x₁ ，x₂ ， x₃可以构成“和谐三数组”；

(3)、若A(m ， y₁) ，B(m + 1，y₂) ，C(m+3，y₃)三个点均在反比例函数 $y = \frac{4}{x}$ 的图象上，且三点的纵坐标恰好构成“和谐三数组”，求实数m的值．

查看试题解析

x	0	1	2	3	4
ax²+bx+c	-14.5	-11.5	-6.5	0.5	9.5

北师版数学九年级上册《 第二章 一元二次方程》检测卷B卷

一、单选题

二、填空题

三、解答题

北师版数学九年级上册《第二章一元二次方程》检测卷B卷