北师版数学九年级上册同步训练《2.6 应用一元二次方程》

试卷更新日期：2021-08-28 类型：同步测试

进入出卷网下载

一、单选题

1. 广西北部湾某中学为了使学生能够更好地进行体育活动，决定修建一个长方体形状的游泳池，其底面周长为100 m，设游泳池的底面长方形的长为x m，要使游泳池的底面面积为400 m² ，则可列方程为（　　）

A、x（100-x）=400 B、2x（100-2x）=400 C、x（100-2x）=400 D、x（50-x）=400

查看试题解析
2. 用总长 $10 m$ 的铝合金材料做一个如图所示的窗框（不计损耗），窗框的上部是等腰直角三角形，下部是一个矩形，窗框的总面积为 $3 m^{2}$ （材料的厚度忽略不计）.若设等腰直角三角形的斜边长为 $x m$ ，则下列方程正确的是（）．

A、 $x \cdot (5 - x - \frac{\sqrt{2}}{2} x) + \frac{1}{2} x^{2} = 3$ B、 $x \cdot (5 - x + \frac{\sqrt{2}}{2} x) + \frac{1}{4} x^{2} = 3$ C、 $x \cdot (5 - x + \frac{\sqrt{2}}{2} x) + \frac{1}{2} x^{2} = 3$ D、 $x \cdot (5 - x - \frac{\sqrt{2}}{2} x) + \frac{1}{4} x^{2} = 3$

查看试题解析
3. 用一条长60cm的绳子怎样围成一个面积为200cm²的矩形？设矩形的一边为xcm ，根据题意，可列方程为（）

A、x（30+x）＝200 B、x（30﹣x）＝200 C、x（x+60）＝200 D、x（60﹣x）＝200

查看试题解析
4. 商场购进一批衬衣，进货单价为30元，按40元出售时，每天能售出500件．若每件涨价1元，则每天销售量就减少10件．为了尽快出手这批衬衣，而且还能每天获取8000元的利润，其售价应该定为（）

A、50元 B、60元 C、70元 D、50元或70元

查看试题解析
5. 如图，学校课外小组的试验园地的形状是长30米宽15米的矩形，为便于管理，要在中间开辟一横两纵共三条等宽的小道，使种植面积为392平方米，则小道的宽为多少米？若设小道的宽为x米，则根据题意，列方程为（）

A、 $(30 + 2 x) (15 + x) = 392$ B、 $(30 - 2 x) (15 - x) = 392$ C、 $(30 + x) (15 + 2 x) = 392$ D、 $(30 - x) (15 - 2 x) = 392$

查看试题解析
6. 某花圃用花盆培育某种花苗，经过试验发现，每盆花的盈利与每盆株数构成一定的关系.每盆植入3株时，平均单株盈利5元；以同样的栽培条件，若每盆每增加1株，平均单株盈利就减少0.5元.要使每盆的盈利为20元，需要每盆增加几株花苗？设每盆增加 $x$ 株花苗，下面列出的方程中符合题意的是（）

A、 $(x + 3) (5 - 0.5 x) = 20$ B、 $(x - 3) (5 + 0.5 x) = 20$ C、 $(x - 3) (5 - 0.5 x) = 20$ D、 $(x + 3) (5 + 0.5 x) = 20$

查看试题解析
7. 某工厂生产的某种产品按质量分为10个档次，第1档次（最低档次）的产品一天能生产95件，每件利润6元，每提高一个档次，每件利润增加2元，但一天产量减少5件.若生产的产品一天的总利润为1120元，且同一天所生产的产品为同一档次，则该产品的质量档次是（）

A、6 B、8 C、10 D、12

查看试题解析
8. 一人携带变异新冠状病毒，经过两轮传染后共有 $121$ 人感染，设每轮传染中平均一个人传染了 $x$ 个人，则可列方程（）

A、 $x + x (1 + x) = 121$ B、 $1 + x (x + 1) = 121$ C、 ${(1 + x)}^{2} = 121$ D、 $x (x + 1) = 121$

查看试题解析
9. 由于疫情得到缓和，餐饮行业逐渐回暖，某家餐厅重新开张，开业第一天收入约为3020元，之后两天的收入按相同的增长率增长，第三天收入约为4350元.设每天的增长率为x，根据题意可列方程为（）

A、 $3020 {(1 - x)}^{2} = 4350$ B、 $3020 (1 + 2 x) = 4350$ C、 $3020 {(1 + x)}^{2} = 4350$ D、 $3020 (1 - 2 x) = 4350$

查看试题解析
10. 参加足球联赛的每两支球队之间都要进行两场比赛，共要比赛110场，设参加比赛的球队有x支，根据题意，下面列出的方程正确的是（）

A、 $\frac{1}{2}$ x（x+1）＝110 B、 $\frac{1}{2}$ x（x﹣1）＝110 C、x（x+1）＝110 D、x（x﹣1）＝110

查看试题解析

二、填空题

11. 我国南宋数学家杨辉所著《田亩比类乘除算法》中记载了这样一道题：“直田积八百六十四步，只云阔不及长一十二步，问阔及长各几步。”其大意为：一个矩形的面积为864平方步，宽比长少12步，问宽和长各多少步？设矩形的宽为x步，根据题意，可列方程为。

查看试题解析
12. 我国古代数学名著《算法统宗）有一道“荡秋干”的问题，“平地秋千未起，踏板一尺离地.送行二步与人齐，5尺人高曾记，仕女家人争蹴.良工高士素好奇，算出索长有几？”此问题可理解为：如图，有一架秋千，当它静止时，踏板离地距离PA的长为1尺，将它向前水平推送10尺时，即 $P^{'} C = 10$ 尺，秋千踏板离地的距离 $P^{'} B$ 就和身高5尺的人一样高，秋千的绳索始终拉得很直，则秋千的绳索长为尺.

查看试题解析
13. 由10块相同的小长方形地砖拼成面积为1.6m²的长方形ABCD（如图），则长方形ABCD的周长为．

查看试题解析
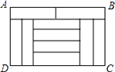14. 如图，在一个长为40 m，宽为26m的矩形花园中修建小道（图中阴影部分），其中 $A B = C D = E F = G H = x m$ ，每段小道的两边缘平行，剩余的地方种植花草，要使种植花草的面积为 $864 m^{2}$ ，那么 $x =$ m.

查看试题解析
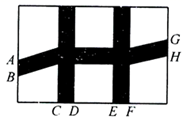15. 某商店销售一批头盔，售价为每顶60元，每月可售出200顶．在“创建文明城市”期间，计划将头盔降价销售，经调查发现：每降价1元，每月可多售出20顶．已知头盔的进价为每顶40元，则该商店每月获得最大利润时，每顶头盔的售价为元．

查看试题解析
16. 一个两位数，个位数字比十位数字大3，个位数的平方恰好等于这个两位数，这个两位数是.

查看试题解析

三、解答题

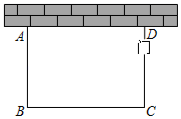
17. 某种肺炎病毒在A国爆发，经世卫组织研究发现：病毒有极强的传染性，一个病毒携带者与10个人有密切接触，其中的6人会感染病毒，成为新的病毒携带者.在调查某工厂的疫情时，发现最初只有1位出差回来的病毒携带者，在召开工厂车间组长会议时发生了第一轮传染，开完会后所有人都回到各自车间工作又发生了第二轮传染，这时全厂一共有169人检测出携带病毒.假如每个病毒携带者每次的密切接触者人数都相同，求每个病毒携带者每次的密切接触了多少人？

查看试题解析
18. 某地为引导旅客来旅游及消费，计划5月至9月开展全城推广活动.某旅行社为吸引市民组团去旅游，推出了如下收费标准：如果人数不超过25人，人均旅游费用为2000元；如果超过25人，每增加1人，人均旅游费用降低40元，但人均旅游费用不得低于1700元.某单位组织员工去旅游，共支付给该旅行社旅游费用54000元，请问该单位这次共有多少员工去旅游？

查看试题解析
19. 列方程（组）解应用题：某驻村工作队，为带动群众增收致富，巩固脱贫攻坚成效，决定在该村山脚下，围一块面积为600m²的矩形试验茶园，便于成功后大面积推广.如图所示，茶园一面靠墙，墙长35m，另外三面用69m长的篱笆围成，其中一边开有一扇1m宽的门（不包括篱笆）.求这个茶园的长和宽.

查看试题解析
20. 2021年7日1日建党100周年纪念日，在本月日历表上可以用一个方框圈出4个数（如图所示），若圈出的四个数中，最小数与最大数的乘积为65，求这个最小数（请用方程知识解答）．

查看试题解析
21. 读诗词解题：（通过列方程式，算出周瑜去世时的年龄）
大江东去浪淘尽，千古风流数人物；

而立之年督东吴，早逝英年两位数；

十位恰小个位三，个位平方与寿符；

哪位学子算得快，多少年华属周瑜？

查看试题解析
22. 某商场销售一批名牌衬衫，当销售价为299元时，平均每天可售出20件，每件盈利40元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经试销发现，如果每件衬衫每降价1元，商场平均每天可多售出2件，若商场平均每天要盈利1200元，每件衬衫定价应多少元？

查看试题解析