北师版数学九年级上册同步训练《2.4 用因式分解法求解一元二次方程》
试卷更新日期:2021-08-28 类型:同步测试
一、单选题
-
1. 方程 的根是( )A、 B、 C、 D、2. 一元二次方程x(x﹣2)=x﹣2的根是( )A、x=2 B、x1=0,x2=2 C、x1=2,x2=1 D、x=﹣13. 方程 的解是( )A、2或0 B、±2或0 C、2 D、-2或04. 已知直角三角形的两条边长分别是方程x2-14x+48=0的两个根,则此三角形的第三边是( )A、6或8 B、10或 C、10或8 D、5. 方程 的解为( )A、 B、 C、 , D、 ,6. 已知实数x满足(x2﹣2x+1)2+4 (x2﹣2x+1)﹣5=0,那么x2﹣2x+1的值为( )A、﹣5或1 B、﹣1或5 C、1 D、57. 方程2x(x﹣3)=5(x﹣3)的根是( )A、x= B、x=3 C、x1= ,x2=3 D、x1=﹣ ,x2=38. 下列说法中,正确的说法有( )
①对角线互相平分且相等的四边形是菱形;
②一元二次方程 的根是 , ;
③两个相似三角形的周长的比为 ,则它们的面积的比为 ;
④对角线互相垂直的平行四边形为正方形;
⑤对角线垂直的四边形各边中点得到的四边形是矩形.
A、1个 B、2个 C、3个 D、4个9. 已知关于x的一元二次方程3x2﹣2xy-y2=0的,则 ( )A、1 B、1或 C、1或﹣ D、﹣10. 如图,在平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x﹣3=0的根,则平行四边形ABCD的周长为( )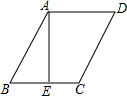 A、12-6 B、6 +12 C、4+2 D、4-2
A、12-6 B、6 +12 C、4+2 D、4-2二、填空题
-
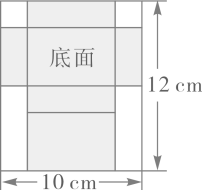
11. 对于任意实数a、b,定义一种运算: ,若 ,则x的值为.12. 如图是一张长 ,宽 的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积 是的有盖的长方体铁盒.则剪去的正方形的边长为 .
 13. 当x=时,代数式x2+4x的值与代数式2x+3的值相等.14. 阅读理解:对于x3﹣(n2+1)x+n这类特殊的代数式可以按下面的方法分解因式:
13. 当x=时,代数式x2+4x的值与代数式2x+3的值相等.14. 阅读理解:对于x3﹣(n2+1)x+n这类特殊的代数式可以按下面的方法分解因式:x3﹣(n2+1)x+n=x3﹣n2x﹣x+n=x(x2﹣n2)﹣(x﹣n)=x(x﹣n)(x+n)﹣(x﹣n)=(x﹣n)(x2+nx﹣1).
理解运用:如果x3﹣(n2+1)x+n=0,那么(x﹣n)(x2+nx﹣1)=0,即有x﹣n=0或x2+nx﹣1=0,
因此,方程x﹣n=0和x2+nx﹣1=0的所有解就是方程x3﹣(n2+1)x+n=0的解.
解决问题:求方程x3﹣5x+2=0的解为 .
15. 已知实数 , , , 满足 ,若 ,则 .16. 数学活动课上,小云和小王在讨论张老师出示的一道代数式求值问题:已知实数a,b同时满足a2+2a=b+2,b2+2b=a+2,求代数式 的值.
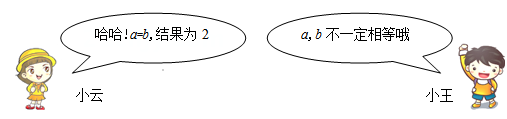
结合他们的对话,请解答下列问题:(1)、当a=b时,a的值是 .(2)、当a≠b时,代数式 的值是 .三、解答题
-
17. 解方程: .18. 解方程: .19. 解方程: .20. 解方程:2(x﹣3)=3x(x﹣3).21. 解方程:x2﹣1=3(x+1).22. 小敏与小霞两位同学解方程3(x﹣3)=(x﹣3)2的过程如下框:
小敏:
两边同除以(x﹣3),得
3=x﹣3,
则x=6.
小霞:
移项,得3(x﹣3)﹣(x﹣3)2=0,
提取公因式,得(x﹣3)(3﹣x﹣3)=0.
则x﹣3=0或3﹣x﹣3=0,
解得x1=3,x2=0.
你认为他们的解法是否正确?若正确请在框内打“√”;若错误请在框内打“×”,并写出你的解答过程.
23. 阅读例题,解答下题.范例:解方程:x2+∣x+1∣﹣1=0
解:⑴当x+1≥0,即x≥﹣1时,
x2+x+1﹣1=0
x2+x=0
解得x1=0 , x2=﹣1
⑵当x+1<0,即x<﹣1时,
x2﹣(x+1)﹣1=0
x2﹣x﹣2=0
解得x1=﹣1,x2=2
∵x<﹣1,∴x1=﹣1,x2=2都舍去.
综上所述,原方程的解是x1=0,x2=﹣1
依照上例解法,解方程:x2﹣2∣x-2∣-4=0
24. 如表:方程1、方程2、方程3、…是按一定规律排列的一列方程.序号
方程
方程的解
1
x2+x﹣2﹣=0
x1=﹣2
x2=1
2
x2+2x﹣8﹣=0
x1=﹣4
x2=2
3
x2+3x﹣18=0
x1=
x2=
…
…
…
…
(1)、解方程3,并将它的解填在表中的空白处;(2)、请写出这列方程中第10个方程,并用求根公式求其解.(3)、根据表中的规律写出第n个方程和这个方程的解.