北师版数学九年级上册同步训练《2.2 用配方法求解一元二次方程》

试卷更新日期：2021-08-28 类型：同步测试

进入出卷网下载

一、单选题

1. 用配方法解方程 $x^{2} - 8 x + 11 = 0$ 的过程中，配方正确的是（）

A、 $x^{2} - 8 x + {(- 4)}^{2} = 5$ B、 $x^{2} - 8 x + {(- 4)}^{2} = 31$ C、 ${(x + 4)}^{2} = 5$ D、 ${(x - 4)}^{2} = - 11$

查看试题解析
2. 用配方法解方程x²+4x+1＝0时，配方结果正确的是（）

A、（x﹣2）²＝5 B、（x﹣2）²＝3 C、（x+2）²＝5 D、（x+2）²＝3

查看试题解析
3. 一元二次方程 $4 x^{2} - 4 x - 3 = 0$ 配方后可化为（）

A、 ${(x + \frac{1}{2})}^{2} = 1$ B、 ${(x - \frac{1}{2})}^{2} = 1$ C、 ${(x + \frac{1}{2})}^{2} = \frac{3}{4}$ D、 ${(x - \frac{1}{2})}^{2} = \frac{3}{4}$

查看试题解析
4. 将一元二次方程 $x^{2} - 2 x = 1$ 配方，其正确的结果是（）

A、 ${(x + 1)}^{2} = 2$ B、 ${(x - 2)}^{2} = 5$ C、 ${(x - 1)}^{2} = 1$ D、 ${(x - 1)}^{2} = 2$

查看试题解析
5. 若用配方法解一元二次方程 $x^{2} - 4 x - 5 = 0$ ，则方程可变形为（　　）

A、 ${(x + 2)}^{2} = 9$ B、 ${(x - 2)}^{2} = 9$ C、 ${(x + 2)}^{2} = 1$ D、 ${(x - 2)}^{2} = 1$

查看试题解析
6. 一元二次方程2x²＋6x＋3＝ 0 经过配方后可变形为（）

A、 ${(x + \frac{3}{2})}^{2} = \frac{3}{4}$ B、 ${(x + 3)}^{2} = 6$ C、 ${(x - 3)}^{2} = 12$ D、 ${(x - \frac{3}{2})}^{2} = \frac{15}{4}$

查看试题解析
7. 下列用配方法解方程 $\frac{1}{2} x^{2} - x - 2 = 0$ 的四个步骤中，出现错误的是（）

A、① B、② C、③ D、④

查看试题解析
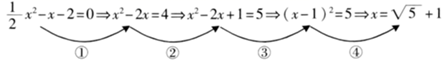8. 把方程 $x^{2} - 4 x - 6 = 0$ 配方成 ${(x + m)}^{2} = n$ 的形式，结果应是（）

A、 ${(x - 4)}^{2} = 2$ B、 ${(x - 2)}^{2} = 6$ C、 ${(x - 2)}^{2} = 8$ D、 ${(x - 2)}^{2} = 10$

查看试题解析
9. 用配方法解下列方程时，配方错误的是（）

A、 $x^{2} + 2 x - 99 = 0$ 化为 $（ x + 1 ）^{2} = 100$ B、 $2 x^{2} - 8 x - 4 = 0$ 化为 $（ x - 2 ）^{2} = 6$ C、 $x^{2} + 8 x + 9 = 0$ 化为 $（ x + 4 ）^{2} = 25$ D、 $3 x^{2} - 4 x - 2 = 0$ 化为 $（ x - \frac{2}{3} ）^{2} = \frac{10}{9}$

查看试题解析
10. 若用配方法解方程 $4 x^{2} + 12 x = 1$ ，通常要在此方程两边同时加上一个“适当”的数，则下面变形恰当的是（）

A、 $4 x^{2} + 12 x + {(\frac{12}{2})}^{2} = 1 + {(\frac{12}{2})}^{2}$ B、 $4 x^{2} + 12 x + 12^{2} = 1 + 12^{2}$ C、 $4 x^{2} + 12 x + 9 = 1 + 9$ D、 $4 x^{2} + 12 x + 12 = 1 + 12$

查看试题解析

二、填空题

11. 将一元二次方程 $x^{2} - 3 x + 1 = 0$ 变形为 ${(x + h)}^{2} = k$ 的形式为.

查看试题解析
12. 当 $x =$ 时，代数式 $3 x^{2} - 6 x$ 的值等于 $12$ ．

查看试题解析
13. 当 $x =$ 时，代数式 $x^{2} - x$ 与 $x - 1$ 的值相等.

查看试题解析
14. 用配方法解方程 $\frac{1}{2} x^{2} + x - \frac{5}{2} = 0$ 时，可配方为 $\frac{1}{2} [{(x + 1)}^{2} + k] = 0$ ，其中 $k =$ .

查看试题解析
15. 一元二次方程x²-ax+6=0, 配方后为(x-3)²=3, 则a=.

查看试题解析
16. 规定： $a \otimes b = (a + b) b$ ，如： $2 \otimes 3 = (2 + 3) \times 3 = 15$ ，若 $2 \otimes x = 3$ ，则 $x$ ＝.

查看试题解析

三、解答题

17. 解方程： $\frac{1}{2}$ x²﹣x﹣1＝0．

查看试题解析
18. 用配方法解方程： $x^{2} + 27 = 12 x$ .

查看试题解析
19. 用配方法解方程： $x^{2} + 4 x - 8 = 0$ .

查看试题解析
20. 用配方法解方程2x²-6x+1=0

查看试题解析
21. 解方程：2x²﹣5x+1=0

查看试题解析
22. 已知多项式 $A = {(x + 2)}^{2} + x (1 - x) - 9$ ．

(1)、化简多项式 $A$ 时，小明的结果与其他同学的不同，请你检查小明同学的解题过程．在标出①②③④的几项中出现错误的是；请写出正确的解答过程．

(2)、小亮说：“只要给出 $x^{2} - 2 x + 1$ 的合理的值，即可求出多项式 $A$ 的值．”小明给出 $x^{2} - 2 x + 1$ 值为4，请你求出此时 $A$ 的值．
小明的作业

解： $A = {(x + 2)}^{2} + x (1 - x) - 9$

$\begin{array}{l} = x^{2} \underline{+ 2 x} \underline{+ 4} \underline{+ x} \underline{- x^{2}} - 9 \\ ① ② ③ ④ \end{array}$

$= 3 x - 5$

查看试题解析
23. 根据要求，解答下列问题．

(1)、根据要求，解答下列问题．
①方程x²－2x＋1＝0的解为；

②方程x²－3x＋2＝0的解为；

③方程x²－4x＋3＝0的解为；

…… ……

(2)、根据以上方程特征及其解的特征，请猜想：
①方程x²－9x＋8＝0的解为；

②关于x的方程的解为x₁＝1，x₂＝n．

(3)、请用配方法解方程x²－9x＋8＝0，以验证猜想结论的符合题意性．

查看试题解析
24. 阅读资料：阅读材料，完成任务：材料阿尔·花拉子密(约 780～约 850)，著名数学家、天文学家、地理学家，是代数与算术的整理者，被誉为“代数之父”。

他用以下方法求得一元二次方程 x²＋2x－35＝0 的解：

将边长为 x 的正方形和边长为 1 的正方形，外加两个长方形，长为 x ，宽为 1，拼合在一起的面积是 x²＋2×x×1＋1×1，而由 x²＋2x－35＝0 变形得 x²＋2x＋1＝35＋1（如图所示），即右边边长为 x＋1 的正方形面积为 36。

所以(x＋1)²＝36，则 x＝5.

任务：请回答下列问题

(1)、上述求解过程中所用的方法是（）

A、直接开平方法 B、公式法 C、配方法 D、因式分解法

(2)、所用的数学思想方法是（）

A、分类讨论思想 B、数形结合思想 C、转化思想 D、公理化思想

(3)、运用上述方法构造出符合方程 x²＋8x－9＝0 的一个正根的正方形

查看试题解析