初中数学湘教版九年级上册3.5相似三角形的应用 同步练习
试卷更新日期：2021-08-27 类型：同步测试
一、单选题
-
1. 如图，一同学在湖边看到一棵树，他目测出自己与树的距离为20m，树的顶端在水中的倒影距自己5m远，该同学的身高为1.7m，则树高为（ ）m.
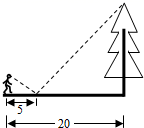A、3.4 B、5.1 C、6.8 D、8.52. 如图，放映幻灯片时，通过光源，把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为30cm，光源到屏幕的距离为90cm，且幻灯片中的图形的高度为7cm，则屏幕上图形的高度为（ ）
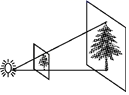A、21cm B、14cm C、6cm D、24cm3. 如图，树AB在路灯O的照射下形成投影AC，已知路灯高 ，树影 ，树AB与路灯O的水平距离 ，则树的高度AB长是（ ）
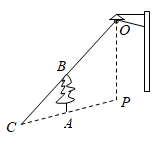A、 B、 C、 D、4. 图1是装了液体的高脚杯示意图（数据如图），用去一部分液体后如图2所示，此时液面 （ ）
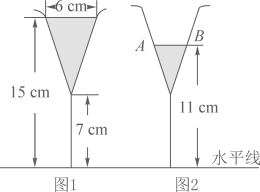A、 B、 C、 D、5. 某数学活动小组在利用太阳光线测量某棵树 的高度时，发现树 的影子不全落在地面上，有一部分影子落在教学楼的墙壁上.经测量，落在墙壁上影高 为2米，落在地面上的影长 为5米，同一时间测得8米高的国旗杆影长是4米，则树高为（ ）
A、8米 B、10米 C、12米 D、14米6. 如图，将 沿 边上的中线 平移到 的位置．已知 的面积为16，阴影部分三角形的面积9．若 ，则 等于（ ）
A、2 B、3 C、4 D、7. 一个三角形框架模型的三边长分别为20厘米、30厘米、40厘米，木工要以一根长为60厘米的木条为一边，做一个与模型三角形相似的三角形，那么另两条边的木条长度不符合条件的是（ ）
A、30厘米、45厘米； B、40厘米、80厘米； C、80厘米、120厘米； D、90厘米、120厘米8. 如图是小明设计用手电来测量某古城墙高度的示意图．点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD ， CD⊥BD ， 且测得AB=1.2米，BP=1.8米，PD=12米，那么该古城墙的高度是（ ）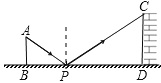
A、6米 B、8米 C、18米 D、24米9. 中国古代在利用“计里画方”（比例缩放和直角坐标网格体系）的方法制作地图时，会利用测杆、水准仪和照板来测量距离．在如图所示的测量距离AB的示意图中，记照板“内芯”的高度为EF，观测者的眼睛（图中用点C表示）与BF在同一水平线上，则下列结论中，正确是（ ）
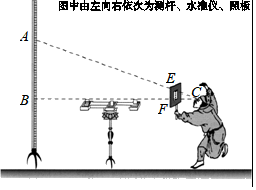A、 B、 C、 D、10. 如图所示，某超市在一楼至二楼之间安装有电梯，天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好安全通过，请你根据图中数据回答，两层楼之间的高约为（ ）
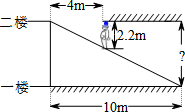A、 B、 C、11m D、二、填空题
-
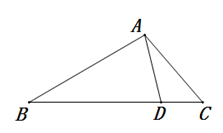
11. 如图，在 中， ， ， 为 边上的一点，且 .若 的面积为1，则 的面积为.
12. 如图是用卡钳测量容器内径的示意图，现量得卡钳上 ， 两个端点之间的距离为 ， ，则容器的内径是.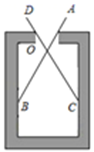
13. 学习投影后，小华利用灯光下自己的影子长度来测量一路灯的高度.如图，身高1.7m的小明从路灯灯泡A的正下方点B处，沿着平直的道路走8m到达点D处，测得影子DE长是2m，则路灯灯泡A离地面的高度AB为m.
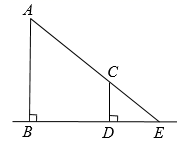14. 如图，为了测量山坡的护坡石坝高，把一根长为 的竹竿 斜靠在石坝旁，量出竿上 长为 时，它离地面的高度 为 ，则坝高 为 ．
15. 墙壁CD上D处有一盏灯（如图），小明站在A站测得他的影长与身长相等都为1.5m，他向墙壁走1m到B处时发现影子刚好落在A点，则灯泡与地面的距离CD=m.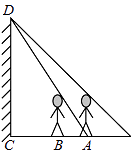
16.如图，李明打网球时，球恰好打过网，且落在离网4m的位置上，则网球的击球的高度h为 ．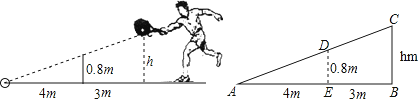
三、计算题
-
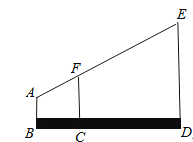
17.
如图，某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上，已知此人的眼睛到地面的距离AB=1.6m，标杆FC=2.2m，且BC=1m，CD=5m，标杆FC、ED垂直于地面．求电视塔的高ED．
四、解答题
-
18. 如图，某学习小组为了测量校园内一棵小树的高度 ，用长为 的竹竿 作测量工具，移动竹竿，使竹竿影子的顶端、树影子的顶端落在水平地面上的同一点E，且点E，A，C在同一直线上.已知 ， ，求这棵树的高度 .
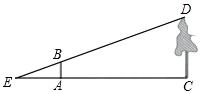19. 如图，利用标杆 测量楼高，点A，D，B在同一直线上， ， ，垂足分别为E，C.若测得 ， ， ，楼高 是多少？
20. “今有邑，东西七里，南北九里，各开中门，出东门一十五里有木，问：出南门几何步而见木？”这段话摘自《九章算术》，意思是说：如图，矩形城池ABCD ， 东边城墙AB长9里，南边城墙AD长7里，东门点E ， 南门点F分别是AB、AD的中点，EG⊥AB ， FH⊥AD ， EG＝15里，HG经过点A ， 问FH多少里？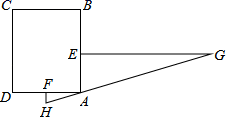
五、作图题
-
21. 已知：如图，AB和DE是直立在地面上的两根立柱，AB＝5m，某一时刻，AB在阳光下的投影BC＝4m.
(1)、请你在图中画出此时DE在阳光下的投影；(2)、在测量AB的投影长时，同时测出DE在阳光下的投影长为6m，请你计算DE的长.22. 如图，在路灯下，小明的身高如图中线段AB所示，他在地面上的影子如图中线段AC所示，小亮的身高如图中线段FG所示，路灯灯泡在线段DE上。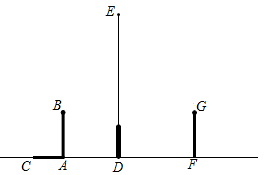
(1)、请你确定灯泡所在的位置，并画出小亮在灯光下形成的影子。(用线段表示)(2)、如果小明的身高AB=1.6m，他的影子长AC=1.4m，且他到路灯的距离AD=2.1m，求灯泡的高。六、综合题
-
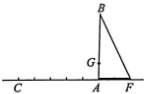
23. 如图，已知小屋的高 ，小屋窗户的最低点G距离地面 ，某一时刻， 在阳光下的影长 ，在点A的正西方向 处选择点C，在此处拟建高为 的楼房 .（设点C、A、F在同一水平线上）
(1)、按比例较准确地画出楼房 及同一时刻它的影长；(2)、若楼房 建成后，请判断是否影响小屋的采光，并说明理由.24. 如图所示，身高1.5米的小明从路灯下的A点经过，测量得身后的影子 的长5米，沿 所在的直线行走10米到B点时，身后的影子 长为2米.
(1)、请你确定路灯P的位置(2)、求路灯P距到地面的距离.25. 在△ABC中，∠ACB＝90°，BC＝3，AC＝4，点O是AB的中点，点D是边AC上一点，DE⊥BD，交BC的延长线于点E，OD⊥DF，交BC边于点F，过点E作EG⊥AB，垂足为点G，EG分别交BD、DF、DC于点M、N、H．
(1)、求证： ；(2)、设CD＝x，NE＝y，求y关于x的函数关系式及其定义域；(3)、当△DEF是以DE为腰的等腰三角形时，求线段CD的长．
-