浙江省宁波市九校2020-2021学年高一下学期数学期末联考试卷

试卷更新日期：2021-08-27 类型：期末考试

进入出卷网下载

一、单选题

1. 复数 $z = \frac{1 + i}{1 - 2 i}$ 在复平面内对应的点在第（）象限

A、一 B、二 C、三 D、四

查看试题解析
2. 已知 $\vec{a} = (2 m ， 2)$ ， $\vec{b} = (3 ， m)$ ，若 $\vec{a} / / \vec{b}$ ，则 $m =$ （）

A、 $\sqrt{3}$ B、 $- \sqrt{3}$ C、 $\pm \sqrt{3}$ D、3

查看试题解析
3. 某小区有500人自愿接种新冠疫苗，其中49~59岁的有140人，18~20岁的有40人，其余为符合接种条件的其他年龄段的居民．在一项接种疫苗的追踪调查中，要用分层抽样的方法从该小区500名接种疫苗的人群中抽取50人，则从符合接种条件的其他年龄段的居民中抽取的人数是（）

A、14 B、18 C、32 D、50

查看试题解析
4. 设 $α$ 、 $β$ 是两个不同的平面，m、n是两条不同的直线，下列说法正确的是（）

A、若 $α ⊥ β$ ， $α \cap β = m$ ， $m ⊥ n$ ，则 $n ⊥ β$ B、若 $α ⊥ β$ ， $n / / α$ ，则 $n ⊥ β$ C、若 $m / / α$ ， $m / / β$ ，则 $α / / β$ D、若 $m ⊥ α$ ， $m ⊥ β$ ， $n ⊥ α$ ，则 $n ⊥ β$

查看试题解析
5. 北碚区在创建“全国文明城市”活动中大力加强垃圾分类投放宣传．某居民小区设有“厨余垃圾”、“可回收垃圾”、“其它垃圾”、“有害垃圾”四种不同的垃圾桶．一天，居民小陈提着上述分好类的垃圾各一袋，随机每桶投一袋，则恰好有两袋垃圾投对的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{9}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
6. 如图，已知 $B D$ 为 $△ A B C$ 中 $∠ A B C$ 的角平分线，若 $B C = 2 A B = 2$ ， $∠ A B C = \frac{π}{3}$ ，则 $\vec{B D} \cdot \vec{A C} =$ （）

A、1 B、2 C、3 D、 $\frac{3}{2}$

查看试题解析
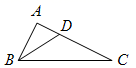7. 古代数学名著《九章算术・商功》中，将底面为矩形且有一条侧棱与底面垂直的四棱锥称为阳马，将四个面都为直角三角形的三棱锥称为鳖臑．若四棱锥 $P - A B C D$ 为阳马， $P A ⊥$ 平面 $A B C D$ ， $A B = B C = 4$ ， $P A = 3$ ，则此“阳马”外接球与内切球的表面积之比为（）

A、 $\frac{\sqrt{41}}{2}$ B、 $\frac{41}{4}$ C、 $\sqrt{41}$ D、 $41$

查看试题解析
8. 如图，等腰梯形 $A B C D$ 中， $A B / / C D$ ， $A B = 2$ ， $A D = B C = 1$ ， $A B > C D$ ，沿着 $A C$ 把 $△ A C D$ 折起至 $△ A C D_{1}$ ，使 $D_{1}$ 在平面 $A B C$ 上的射影恰好落在 $A B$ 上．当边长 $C D$ 变化时，点 $D_{1}$ 的轨迹长度为（）

A、 $\frac{π}{2}$ B、 $\frac{π}{3}$ C、 $\frac{π}{4}$ D、 $\frac{π}{6}$

查看试题解析

二、多选题

9. 从装有4个红球和3个白球的口袋中任取4个球，那么互斥而不对立的事件是（）

A、恰有1个红球与恰有2个红球 B、至少有1个白球与都是红球 C、恰有1个红球与恰有1个白球 D、至少有1个红球与至少有1白球

查看试题解析
10. 关于平面向量，下列说法正确的是（）

A、若 $\vec{a} / / \vec{b}$ ， $\vec{b} / / \vec{c}$ ，则 $\vec{a} / / \vec{c}$ B、已知 $\vec{a} = (2 ， 1)$ ， $\vec{b} = (3 ， 4)$ ，则 $\vec{a}$ 在 $\vec{b}$ 方向上的投影向量是 $(\frac{6}{5} ， \frac{8}{5})$ C、若 $\vec{a} = (λ ， 1)$ ， $\vec{b} = (1 - λ ， 2)$ ，且 $\vec{a}$ 与 $\vec{b}$ 的夹角为锐角，则 $λ \in (- 1 ， 2)$ D、若 $\vec{O A} + \vec{O C} = \vec{O B} + \vec{O D}$ ，且 $\frac{\vec{A B}}{| \vec{A B} |} + \frac{\vec{A D}}{| \vec{A D} |} = \frac{\vec{A C}}{| \vec{A C} |}$ ，则四边形 $A B C D$ 为菱形

查看试题解析
11. 已知 $△ A B C$ 的三个内角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，则下列条件能推导出 $△ A B C$ 一定是锐角三角形的是（）

A、 $a^{2} + b^{2} > c^{2}$ B、 $\frac{\sin A}{5} = \frac{\sin B}{6} = \frac{\sin C}{7}$ C、 $\cos^{2} A + \cos^{2} B - \cos^{2} C = 1$ D、 $\tan A + \tan B + \tan C > 0$

查看试题解析
12. 正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 棱长为 $1$ ，若 $P$ 是空间异于 $C_{1}$ 的一个动点，且 $P C_{1} ⊥ B D_{1}$ ，则下列正确的是（）

A、 $P C_{1} / /$ 平面 $A C B_{1}$ B、存在唯一一点 $P$ ，使 $P D_{1} / / B_{1} C$ C、存在无数个点 $P$ ，使 $P D_{1} ⊥ B_{1} C$ D、若 $P A ⊥ P C$ ，则点 $P$ 到直线 $A_{1} C_{1}$ 的最短距离为 $\frac{\sqrt{6}}{6}$

查看试题解析

三、填空题

13. 设 $z \in C$ ，若 $| z | = 2$ ，则 $| z + i |$ 的最大值为．

查看试题解析
14. 已知三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，棱长均为 $2$ ，顶点 $A_{1}$ 在底面 $A B C$ 上的射影恰为 $A B$ 的中点 $D$ ， $E$ 为 $A C$ 的中点，则直线 $B E$ 与直线 $A B_{1}$ 所成角的余弦值为．

查看试题解析
15. 平面向量 $\vec{a_{i}}$ 满足： $| \vec{a_{i}} | = 1 (i = 0 ， 1 ， 2 ， 3)$ ，且 $\sum_{i = 1}^{3} \vec{a_{i}} = \vec{0}$ ．则 $| \vec{a_{0}} + \vec{a_{1}} + \vec{a_{2}} | + | \vec{a_{0}} + \vec{a_{1}} + \vec{a_{3}} | + | \vec{a_{0}} + \vec{a_{2}} + \vec{a_{3}} |$ 的取值范围为．

查看试题解析
16. 随机事件 $A$ ， $B$ 的概率分别为 $P (A) = 0.5$ ， $P (B) = 0.3$ ．

(1)、若 $B \subseteq A$ ，则 $N (u ， σ^{2})$ ；

(2)、若 $A$ 与 $B$ 相互独立，则 $P (A \cup B) =$ ．

查看试题解析

四、解答题

17. 某企业有甲、乙两个研发小组，他们研发新产品成功的概率分别为 $\frac{2}{3}$ 和 $\frac{3}{4}$ ．现安排甲组研发新产品A，乙组研发新产品B，设甲、乙两组的研发相互独立．

(1)、求至少有一种新产品研发成功的概率；

(2)、若新产品A研发成功，预计企业可获利润120万元；若新产品B研发成功，预计企业可获利润100万元，该企业获得利润超过100万元的概率为多少．

查看试题解析
18. 某校对100名高一学生的某次数学测试成绩进行统计，分成[50，60)，[60，70)，[70，80)，[80，90)，[90，100]五组，得到如图所示频率分布直方图．

(1)、求图中a的值；

(2)、估计该校学生数学成绩的平均数；

(3)、估计该校学生数学成绩的第75百分位数．

查看试题解析
19. 在① $\sqrt{3} (b \cos C - a) = c \sin B$ ；② $2 a + c = 2 b \cos C$ ；③ $b \sin A = \sqrt{3} a \sin \frac{A + C}{2}$ 这三个条件中任选一个，补充在下面问题中的横线上，并解答相应的问题.
在 $Δ A B C$ 中，内角A，B，C的对边分别为a，b，c，且满足 ▲ ， $b = 2 \sqrt{3} ，$ $a + c = 4$ ，求 $Δ A B C$ 的面积.

查看试题解析
20. 如图，在等腰梯形 $A B C D$ 中， $A B / / C D$ ， $A D = D C = C B = \frac{1}{2} A B$ ．点 $P$ 是线段 $D C$ 上的动点．

(1)、若 $\vec{A C} = x \vec{A B} + y \vec{A D}$ ，求 $x$ ， $y$ 的值；

(2)、若 $\vec{A C} = λ \vec{A P} + μ \vec{B D}$ ，求 $λ μ$ 的取值范围．

查看试题解析
21. 如图，已知四边形 $A B C D$ 是菱形， $△ A B E$ 是边长为 $1$ 的正三角形， $F$ 为 $E C$ 的中点，又 $A E ⊥ B F ， E B ⊥ B C$

(1)、求证： $A C ⊥ D F$ ；

(2)、求直线 $A E$ 与平面 $A B C$ 所成角的正弦值．

查看试题解析
22. 在棱长均为 $2$ 的正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $E$ 为 $B_{1} C_{1}$ 的中点．过 $A E$ 的截面与棱 $B B_{1}$ ， $A_{1} C_{1}$ 分别交于点 $F$ ， $G$ ．

(1)、若 $F$ 为 $B B_{1}$ 的中点，求三棱柱被截面 $A G E F$ 分成上下两部分的体积比 $\frac{V_{1}}{V_{2}}$ ；

(2)、若四棱雉 $A_{1} - A G E F$ 的体积为 $\frac{7 \sqrt{3}}{12}$ ，求截面 $A G E F$ 与底面 $A B C$ 所成二面角的正弦值；

(3)、设截面 $A F E G$ 的面积为 $S_{0}$ ， $Δ A E G$ 面积为 $S_{1}$ ， $△ A E F$ 面积为 $S_{2}$ ，当点 $F$ 在棱 $B B_{1}$ 上变动时，求 $\frac{S_{0}^{2}}{S_{1} S_{2}}$ 的取值范围．

查看试题解析