浙江省丽水市2020-2021学年高一下学期数学期末考试试卷
试卷更新日期:2021-08-27 类型:期末考试
一、单选题
-
1. 复数 的虚部为( )A、-1 B、1 C、2 D、2. 先后抛掷一枚质地均匀的硬币两次,得到一次正面向上和一次反面向上的概率为( )A、 B、 C、 D、3. 已知平面向量 , , ,下列结论中正确的是( )A、若 ,则 B、若 ,则 C、若 , ,则 D、若 ,则4. 已知某19个数据的平均数为5,方差为2,现加入一个数5,此时这20个数据的平均数为 ,方差为 ,则( )A、 , B、 , C、 , D、 ,5. 从装有2个红球、4个白球的袋子中任意摸出2个球,事件A=“至少有1个红球”,事件B=“至多有1个白球”,则( )A、 B、 C、 D、6. 若向量 , ,则 在 上的投影向量为( )A、 B、 C、1 D、27. 新冠肺炎疫情的发生,我国的三大产业均受到不同程度的影响,其中第三产业中的各个行业都面临着很大的营收压力.2020年7月国家统计局发布了我国上半年国内经济数据,如图所示:图1为国内三大产业比重,图2为第三产业中各行业比重.

以下关于我国上半年经济数据的说法正确的是( )
A、第一产业的生产总值与第三产业中“租赁和商务服务业”的生产总值基本持平 B、第一产业的生产总值超过第三产业中“房地产业”的生产总值 C、若“住宿餐饮业”生产总值为7500亿元,则“金融业”生产总值为32500亿元 D、若“金融业”生产总值为41040亿元,则第二产业生产总值为166500亿元8. 已知 的外接圆圆心为 ,且 , ,则 ( )A、 B、 C、 D、二、多选题
-
9. 设 , 是两条不同的直线, , 是不同的平面,则下列结论正确的是( )A、若 , ,则 B、若 , , ,则 C、若 , , ,则 D、若 , , ,则10. 下列四个命题中,不正确的是( )A、若复数z满足 ,则 B、若复数 , 满足 ,则 C、若复数 ( ),则 为纯虚数的充要条件是 D、若 ,则11. 已知某地区有小学生120000人,初中生75000人,高中生55000人,当地教育部门为了了解本地区中小学生的近视率,按小学生、初中生、高中生进行分层抽样,抽取一个容量为2000的样本,得到小学生,初中生,高中生的近视率分别为30%,70%,80%.下列说法中正确的有( )A、从高中生中抽取了440人 B、每名学生被抽到的概率为 C、估计该地区中小学生总体的平均近视率为60% D、估计高中学生的近视人数约为4400012. 已知正方体 的棱长为4,点 是 的中点,点 是侧面 内的动点,且满足 ,下列选项正确的是( )
 A、动点 轨迹的长度是 B、三角形 在正方体内运动形成几何体的体积是 C、直线 与 所成的角为 ,则 的最小值是 D、存在某个位置 ,使得直线 与平面 所成的角为
A、动点 轨迹的长度是 B、三角形 在正方体内运动形成几何体的体积是 C、直线 与 所成的角为 ,则 的最小值是 D、存在某个位置 ,使得直线 与平面 所成的角为三、填空题
-
13. 空气质量指数(AQI)是定量描述空气质量状况的无量纲指数,AQI的数值越大、级别和类别越高,说明空气污染状况越严重.当空气质量指数在0\sim 50时,空气质量指数级别为一级(优);当空气质量指数在51-100时,空气质量指数级别为二级(良)……为了加强环境保护,治理空气污染,环境监测部门对我市2020年的空气质量进行调研,随机抽取了100天的空气质量指数(AQI),得下表:
空气质量指数
[0,30]
(30,40]
(40,50]
(50,60]
(60,70]
(70,80]
(80,100]
>100
天数
8
21
22
18
17
8
5
1
依据上表,估计我市某一天的空气质量指数级别为一级(优)的概率是 .
14. 设复数 ,则 .15. 在锐角 中,角 的对边分别为 ,若 , ,则边 的取值范围是 .16. 已知球 的球面面积为 ,四面体 的四个顶点均在球面上,且 平面 , , ,则该四面体的体积的最大值是 .17. 已知平面向量 , ,满足 , , ,则 的最大值是 .18. 已知复数 满足 ,则 的最大值是 .四、解答题
-
19. 某景区的平面图如图所示,其中 , 为两条公路, , 为公路上的两个景点,测得 km, km,为了拓展旅游业务,拟在景区内建一个观景台 ,为了获得最佳观景效果,要求 对 的视角 .现需要从观景台 到 建造两条观光路线 .
 (1)、求 两地间的直线距离;(2)、求观光线路 长的取值范围.20. 以简单随机抽样的方式从某小区抽取100户居民用户进行用电量调查,发现他们的用电量都在 kW•h之间,进行适当分组后(每组为左闭右开的区间),画出频率分布直方图如图所示.
(1)、求 两地间的直线距离;(2)、求观光线路 长的取值范围.20. 以简单随机抽样的方式从某小区抽取100户居民用户进行用电量调查,发现他们的用电量都在 kW•h之间,进行适当分组后(每组为左闭右开的区间),画出频率分布直方图如图所示. (1)、求直方图中x的值;(2)、估计该小区居民用电量的平均值和中位数;(3)、从用电量落在区间[300,400)内被抽到的用户中任取2户,求至少有1户落在区间[350,400)内的概率.21. 如图,已知在矩形 中, , ,点 是边 的中点, 与 相交于点 ,现将△ 沿 折起,点 的位置记为 ,此时 , 是 的中点.
(1)、求直方图中x的值;(2)、估计该小区居民用电量的平均值和中位数;(3)、从用电量落在区间[300,400)内被抽到的用户中任取2户,求至少有1户落在区间[350,400)内的概率.21. 如图,已知在矩形 中, , ,点 是边 的中点, 与 相交于点 ,现将△ 沿 折起,点 的位置记为 ,此时 , 是 的中点.
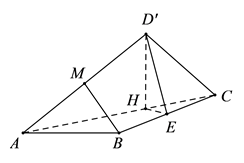 (1)、求证: 平面 ;(2)、求二面角 的余弦值.
(1)、求证: 平面 ;(2)、求二面角 的余弦值.

