浙江省金华十校2020-2021学年高一下学期数学期末考试试卷

试卷更新日期：2021-08-27 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {- 1 ， 1}$ ，下列选项正确的是（）

A、 $1 \in A$ B、 ${- 1} \in A$ C、 $\emptyset \in A$ D、 $0 \in A$

查看试题解析
2. 关于函数 $y = \sin x + \cos x$ ，以下说法正确的是（）

A、在区间 $(0 ， \frac{π}{2})$ 上是增函数 B、在区间 $(0 ， \frac{π}{2})$ 上存在最小值 C、在区间 $(- \frac{π}{2} ， 0)$ 上是增函数 D、在区间 $(- \frac{π}{2} ， 0)$ 上存在最大值

查看试题解析
3. 现有3双不同的鞋子，从中随机取出2只，则取出的鞋都是左脚的概率是（）

A、 $\frac{1}{10}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{5}$

查看试题解析
4. 四名同学各掷骰子5次，记录每次骰子出现的点数并分别对每位同学掷得的点数进行统计处理，在四名同学以下的统计结果中，可以判断出该同学所掷骰子一定没有出现点数1的是（）

A、平均数为4，中位数为5 B、平均数为5，方差为2.4 C、中位数为4，众数为5 D、中位数为4，方差为2.8

查看试题解析
5. 通过研究学生的学习行为，心理学家发现，学生的接受能力依赖于老师引入概念和描述所用的时间．若用 $f (x)$ 表示学生掌握和接受概念的能力（ $f (x)$ 越大，表示学生的接受能力越强）， $x$ 表示提出和讲授概念的时间（单位： $\min$ ），长期的实验和分析表明， $f (x)$ 与 $x$ 有以下关系： $f (x) = {\begin{array}{l} - 0.1 x^{2} + 2.6 x + 43 ， 0 < x \leq 10 ， \\ 59 ， 10 < x \leq 16 ， \\ - 3 x + 107 ， 16 < x \leq 30 ， \end{array}$ 则下列说法错误的是（）

A、讲授开始时，学生的兴趣递增；中间有段时间，学生的兴趣保持较理想的状态；随后学生的注意力开始分散 B、讲课开始后第5分钟比讲课开始第20分钟，学生的接受能力更强一点 C、讲课开始后第10分钟到第16分钟，学生的接受能力最强 D、需要13分钟讲解的复杂问题，老师可以在学生的注意力至少达到55以上的情况下完成

查看试题解析
6. 我国古代数学名著《九章算术》中记载“今有羡除，下广六尺，上广一丈，深三尺，末广八尺，无深，袤七尺．问积几何?”这里的“羡除”，是指由三个等腰梯形和两个全等的三角形围成的五面体．在图1所示羡除中， $A B // C D // E F$ ， $A B = 10$ ， $C D = 8$ ， $E F = 6$ ，等腰梯形 $A B C D$ 和等腰梯形 $A B F E$ 的高分别为7和3，且这两个等腰梯形所在的平面互相垂直．按如图2的分割方式进行体积计算，得该“羡除”的体积为（）

A、84 B、66 C、126 D、105

查看试题解析
7. 在 $△ A B C$ 中，过中线 $A D$ 的中点 $E$ 任作一直线分别交 $A B$ ， $A C$ 于 $M$ ， $N$ 两点，设 $\vec{A M} = m \vec{A B}$ ， $\vec{A N} = n \vec{A C} (m > 0 ， n > 0)$ ，则（）

A、 $m + n$ 为定值 B、 $m \cdot n$ 为定值 C、 $4 m + n$ 的最小值为 $\frac{9}{4}$ D、 $m + 4 n$ 的最小值为6

查看试题解析
8. 设函数 $f (x)$ 的定义域为 $I$ ，如果对任意 $x_{1} \in I$ ，都存在 $x_{2} \in I$ ，使得 $f (x_{1}) + f (x_{2}) = 0$ ，称函数 $f (x)$ 为“ $D$ 函数”，则下列函数为“ $D$ 函数”的是（）

A、 $f (x) = 3^{x}$ B、 $f (x) = e^{x} + \ln x$ C、 $f (x) = x^{2} - 2 x$ D、 $f (x) = \sin x - \cos x + \sin x \cdot \cos x$

查看试题解析

二、多选题

9. 在 $△ A B C$ 中，角A、B、C所对的边分别是a、b、c，点 $P$ 是其所在平面内一点，（）

A、若 $\vec{P A} + 2020 \vec{P B} + 2021 \vec{P C} = \vec{0}$ ，则点 $P$ 在 $△ A B C$ 的中位线上 B、若 $3 \vec{A P} = \vec{A B} + \vec{A C}$ ，则 $P$ 为 $△ A B C$ 的重心 C、若 $a^{2} + b^{2} > c^{2}$ ，则 $△ A B C$ 为锐角三角形 D、若 $c \cos B = b \cos C$ ，则 $△ A B C$ 是等腰三角形

查看试题解析
10. 甲乙两个质地均匀且完全一样的骰子，同时抛掷这两个骰子一次，记事件 $A$ 为“两个骰子朝上一面的数字之和为奇数”，事件 $B$ 为“甲骰子朝上一面的数字为奇数”，事件 $C$ 为“乙骰子朝上一面的数字为偶数”，则（）

A、事件 $A$ 、 $B$ 是相互独立事件 B、事件 $B$ 、 $C$ 是互斥事件 C、 $P (A) = P (B) = P (C)$ D、 $P (A B C) = \frac{1}{8}$

查看试题解析
11. 下列四个函数中，满足对任意正数 $a$ ， $b$ ， $c$ 都有 $f (a + b + c) \leq f (a) + f (b) + f (c)$ 的是（）

A、 $f (x) = 1 + 2 \sin^{2} x$ B、 $f (x) = 2^{x}$ C、 $f (x) = \sqrt{x}$ D、 $f (x) = \ln (x + 1)$

查看试题解析
12. 已知棱长为 $1$ 的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ ， $E$ 、 $F$ 分别是棱 $A D$ 、 $C D$ 上的动点，满足 $A E = D F$ ，则（）

A、四棱锥 $B_{1} - B E D F$ 的体积为定值 B、四面体 $D_{1} D E F$ 表面积为定值 C、异面直线 $B_{1} E$ 和 $A F$ 所成角为 $90^{\circ}$ D、二面角 $D_{1} - E F - B_{1}$ 始终小于 $60^{\circ}$

查看试题解析

三、填空题

13. $(\sqrt{3} - \sqrt{2} i) (\sqrt{3} + \sqrt{2} i) =$ ．

查看试题解析
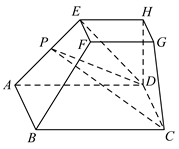
14. 已知某校高一、高二、高三的学生志愿者人数分别为240、160、160．现采用分层抽样的方法从中抽取 $n$ 名同学去某敬老院参加慈善活动，其中高一年级被抽取的人数为12，则 $n =$ ．

查看试题解析
15. 已知 $| \vec{a} | = 2 | \vec{b} | = 2$ ， $\vec{a} \cdot \vec{b} = 1$ ，则 $\vec{a}$ 与 $\vec{a} - \vec{b}$ 的夹角为．

查看试题解析
16. 在四棱台 $A B C D - E F G H$ 中，底面 $A B C D$ 是边长为1的正方形， $D E ⊥$ 平面 $A B F E$ ， $A E = D E$ ， $P$ 为侧棱 $A E$ 上的动点，若二面角 $H - B C - A$ 与二面角 $P - C D - B$ 的大小相等．则 $P A$ 的长为．

查看试题解析

四、解答题

17. 已知函数 $f (x) = 2 \sin^{2} (x + \frac{π}{6}) + \sqrt{3} \sin (2 x + \frac{π}{3}) - 1$ ．

(1)、求函数 $f (x)$ 的周期及图象的对称中心；

(2)、求函数 $f (x)$ 在区间 $[0 ， \frac{π}{2}]$ 上的值域

查看试题解析
18. 在直角坐标系中， $O$ 是坐标原点，向量 $\vec{O A} = (3 ， 1)$ ， $\vec{O B} = (2 ， - 1)$ ， $\vec{O C} = (a ， b)$ ，其中 $a > 0$ ， $b > 0$ ．

(1)、若 $\vec{A B} ⊥ \vec{A C}$ ，求 $\frac{1}{a + 1} + \frac{1}{b}$ 的最小值；

(2)、若 $\vec{O B}$ 与 $\vec{O C}$ 的夹角不超过45°，求 $\frac{b}{a}$ 的取值范围．

查看试题解析
19. 如图，在四棱锥 $P - A B C D$ 中， $A D ⊥$ 平面 $P D C$ ， $A D // B C$ ， $P D ⊥ P B$ ， $A D = 1$ ， $B C = 3$ ， $C D = 4$ ， $P D = 2$ ．

(1)、求证： $P C ⊥ P D$ ；

(2)、求直线 $A B$ 与平面 $P B C$ 所成角的余弦值．

查看试题解析
20. 一家保险公司决定对推销员实行目标管理，即给推销员确定一个具体的销售目标．确定的销售目标是否合适，直接影响到公司的经济效益．如果目标定的过高，多数推销员完不成任务，会使推销员失去信心；如果目标定的太低，将不利于挖掘推销员的工作潜力．该保险公司随机抽取50名保险推销员，统计了其2020年的月均推销额（单位：万元），将数据按照 $[12 ， 14)$ ， $[14 ， 16)$ ，…， $[22 ， 24]$ 分成6组，制成频率分布直方图如下，其中 $[14 ， 16)$ 组比 $[12 ， 14)$ 组的频数多4．

(1)、求频率分布直方图中 $a$ 和 $b$ 的值；

(2)、为调动推销员的积极性，公司设计了两种奖励方案．方案一：奖励月均推销额进入前60%的员工；方案二：奖励月均推销额达到或超过平均数（同一组中的数据用该组区间中点值为代表）的员工．你认为那种方案更好?

查看试题解析
21. 在一大型仓库里，存有大量的原料台球，其大小均匀，按红色与白色分为两堆，每种颜色中又有塑料和木头两种材质，对球进行简单随机抽样，获得抽样数据如下表：

红色

白色

塑料球

木质球

塑料球

木质球

68个

136个

153个

51个

(1)、分别估计等可能地从仓库所有红色球中随机抽取1个得到塑料球的概率，等可能地从仓库所有白色球中随机抽取1个得到塑料球的概率；

(2)、等可能地从仓库所有红色球中依次随机抽取2个，等可能地从仓库所有白色球中随机抽取1个，估计这3个球中恰有2个塑料球的概率．

查看试题解析
22. 函数 $f (x) = | 2^{x} + a - 9 |$ ， $g (x) = - x^{2} + (5 - a) x + 2 a$ ，其中 $a \in R$ ．

(1)、若函数 $g (x)$ 为偶函数，求函数 $f (g (x) - 7)$ 的值域；

(2)、若不存在 $x \in R$ ，使得 $f (x) > 6$ 和 $g (x) > 6$ 同时成立，求 $a$ 的取值范围．

查看试题解析

红色		白色
塑料球	木质球	塑料球	木质球
68个	136个	153个	51个