初中数学湘教版九年级上册3.1比例线段同步练习

试卷更新日期：2021-08-27 类型：同步测试

进入出卷网下载

一、单选题

1. 下面四组线段中，成比例的是（）

A、a=2，b=3，c=4，d=5 B、a=1，b=2，c=2，d=4 C、a=4，b=6，c=8，d=10 D、a= $\sqrt{2}$ ，b= $\sqrt{3}$ ，c=3，d= $\sqrt{3}$

查看试题解析
2. 一杠杆装置如图，杆的一端吊起一桶水，水桶对杆的拉力的作用点到支点的杆长固定不变．甲、乙、丙、丁四位同学分别在杆的另一端竖直向下施加压力F_甲、F_乙、F_丙、F_丁，将相同重量的水桶吊起同样的高度，若F_乙＜F_丙＜F_甲＜F_丁，则这四位同学对杆的压力的作用点到支点的距离最远的是（）

A、甲同学 B、乙同学 C、丙同学 D、丁同学

查看试题解析
3. 古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 $\frac{\sqrt{5} - 1}{2}$ （ $\frac{\sqrt{5} - 1}{2} \approx 0.618$ ，称为黄金分割比例），著名的“断臂维纳斯”便是如此.若小凡的身高满足此黄金分割比例，且肚脐至足底的长度为 $108 cm$ ，则小凡的身高约为（）

A、 $155 cm$ B、 $165 cm$ C、 $175 cm$ D、 $185 cm$

查看试题解析
4. 若 $\frac{a}{b} = \frac{3}{4}$ ，且 $a + b = 14$ ，则 $2 a - b$ 的值是（）

A、2 B、4 C、6 D、8

查看试题解析
5. 下列四组线段中，是成比例线段的是（）

A、2cm，3cm，4cm，5cm B、3cm，6cm，0.2dm，5cm C、2cm，4cm，6cm，8cm D、12cm，8cm，15cm，10cm

查看试题解析
6. 如果 $\frac{a}{b} = \frac{1}{2}$ ，那么 $\frac{a + b}{a - b}$ 的值是（）

A、3 B、-3 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
7. 已知点B是线段AC的黄金分割点（AB＞BC），AC＝10，那么AB的长是（）

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $5 \sqrt{5} - 5$ C、 $5 - \sqrt{5}$ D、 $5 \sqrt{5} - 1$

查看试题解析

二、填空题

8. 如果 $\frac{y}{x}$ ＝ $\frac{1}{3}$ ，那么 $\frac{2 x - y}{y}$ ＝；

查看试题解析
9. 已知 $x : y : z = 2 : 3 : 4$ ，则 $\frac{2 x + y - z}{3 x - 2 y + z} =$ ．

查看试题解析
10. 已知线段c是线段a、b的比例中项，若 $a = 3$ ， $c = 9$ ，则 $b =$ ．

查看试题解析
11. 已知线段AB=10，点C是AB的黄金分割点，且AC＞BC，则AC= .

查看试题解析
12. 已知a，b，c，d是成比例线段，a=3cm，b=2cm，d=6cm，则线段c的长为cm。

查看试题解析
13. 如图，点P是线段AB的黄金分割点，且AP＞BP，设以AP为边长的正方形面积为S₁ ，以PB为宽，以AB为长的矩形面积为S₂ ， S₁S₂（填“ $>$ ”或“ $=$ ”或“ $<$ ”）．

查看试题解析

三、计算题

14. 若a：b=1：2，求（a+b）：a的值．

查看试题解析
15. 已知线段x、y满足 $\frac{2 x + y}{x - y} = \frac{x}{y} ，$ 求 $\frac{x}{y}$ 的值．

查看试题解析

四、解答题

16. 已知线段c是线段a，b的比例中项，若 $a = \sqrt{2}$ ， $b = 8 \sqrt{2}$ ，求线段c的长.

查看试题解析
17. 已知a：b：c＝2：3：5，如果3a－b+c＝24，求a ， b ， c的值．

查看试题解析
18. 实践证明，节目主持人站在舞台的黄金分割点处音响效果及审美效果最好．如下图，假设线段AB为舞台前沿，你能为主持人找出一个最佳位置C吗？

查看试题解析

五、作图题

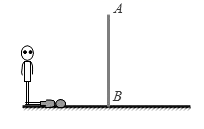
19. 如图，小丽在观察某建筑物 $A B$ ，请你根据小亮在阳光下的投影，画出建筑物 $A B$ 在阳光下的投影.

查看试题解析

六、综合题

20. 阅读理解：
已知：a，b，c，d都是不为0的数，且 $\frac{a}{b} = \frac{c}{d}$ ，求证： $\frac{a + b}{b} = \frac{c + d}{d}$ .

证明：∵ $\frac{a}{b} = \frac{c}{d}$ ，

∴ $\frac{a}{b} + 1 = \frac{c}{d} + 1$ .

∴ $\frac{a + b}{b} = \frac{c + d}{d}$ .

根据以上方法，解答下列问题：

(1)、若 $\frac{a}{b} = \frac{3}{5}$ ，求 $\frac{a + b}{b}$ 的值；

(2)、若 $\frac{a}{b} = \frac{c}{d}$ ，且a≠b，c≠d，证明 $\frac{a - b}{a + b} = \frac{c - d}{c + d}$ .

查看试题解析
21. 在△ABC中，AB＝12，点E在AC上，点D在AB上，若AE＝6，EC＝4， $\frac{A D}{D B} = \frac{A E}{E C}$ 。

(1)、求AD的长；

(2)、试问 $\frac{D B}{A B} = \frac{E C}{A C}$ 能成立吗？请说明理由。

查看试题解析
22. 为了测得图1和图2中旗杆的高度，在太阳光下同一时刻小明和小红分别做了如下操作，测得竹竿 $C D$ 长0.9米，其影长 $C E$ 为1米.

(1)、如图1，若小明测得旗杆影 $A E$ 长为3米，求图1中旗杆高 $A$ B为多少米（ $C D ⊥ A E$ ， $A B ⊥ A E$ ，点 $B$ 、 $D$ 、 $E$ 在一条直线上）；

(2)、如图2，若小红测得旗杆落在地面上的影长 $F G$ 为3米，落在墙上的影子 $G H$ 的高为1.1米，则直接写出图2中旗杆高 $F P$ 为米（ $P F ⊥ F G$ ， $H G ⊥ F G$ ）.

查看试题解析

初中数学湘教版九年级上册3.1比例线段 同步练习

一、单选题

二、填空题

三、计算题

四、解答题

五、作图题

六、综合题

初中数学湘教版九年级上册3.1比例线段同步练习