2022年苏科版初中数学《中考一轮复习》专题二 方程与不等式 2.5 解不等式(组)
试卷更新日期:2021-08-27 类型:一轮复习
一、单选题
-
1. 下列是一元一次不等式的有
, , , , , , .
A、1个 B、2个 C、3个 D、4个2. 下列说法错误的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则3. 一个不等式的解在数轴上表示如图,则这个不等式可以是( )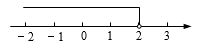 A、 B、 C、 D、4. 若关于x的不等式组 恰有3个整数解,则实数a的取值范围是( )A、 B、 C、 D、5. 不等式组 的解集在以下数轴表示中正确的是( )A、
A、 B、 C、 D、4. 若关于x的不等式组 恰有3个整数解,则实数a的取值范围是( )A、 B、 C、 D、5. 不等式组 的解集在以下数轴表示中正确的是( )A、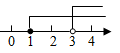 B、
B、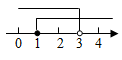 C、
C、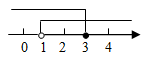 D、
D、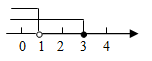 6. 若 是关于x的不等式 的一个解,则a的取值范围是( )A、 B、 C、 D、7. 已知 是方程 的解,那么关于 的不等式 解集是( )A、 B、 C、 D、8. 如果关于x的分式方程 =1+ 有正整数解,且关于y的一元一次不等式组 的解集为y≤a,则所有满足条件的整数a的和为( )A、8 B、7 C、3 D、29. 已知关于x的不等式组 无实数解,则a的取值范围是( )A、 B、 C、 D、10. 对非负实数n“四舍五入”到个位的值记为 ,即:当n为非负整数时,如果 ,则 .反之,当n为非负整数时,如果 时,则 ,如 , , , ,…若关于x的不等式组 的整数解恰有3个,则a的范围()A、1.5≤a<2.5 B、0.5<a≤1.5 C、1.5<a≤2.5 D、0.5≤a<1.5
6. 若 是关于x的不等式 的一个解,则a的取值范围是( )A、 B、 C、 D、7. 已知 是方程 的解,那么关于 的不等式 解集是( )A、 B、 C、 D、8. 如果关于x的分式方程 =1+ 有正整数解,且关于y的一元一次不等式组 的解集为y≤a,则所有满足条件的整数a的和为( )A、8 B、7 C、3 D、29. 已知关于x的不等式组 无实数解,则a的取值范围是( )A、 B、 C、 D、10. 对非负实数n“四舍五入”到个位的值记为 ,即:当n为非负整数时,如果 ,则 .反之,当n为非负整数时,如果 时,则 ,如 , , , ,…若关于x的不等式组 的整数解恰有3个,则a的范围()A、1.5≤a<2.5 B、0.5<a≤1.5 C、1.5<a≤2.5 D、0.5≤a<1.5二、填空题
-
11. 在平面直角坐标系中,若点 在第二象限,则整数m的值为.12. 如果x>y,且(a-1)x<(a-1)y,那么a的取值范围是 .13. 已知x=3是关于x的方程kx+b=0(k≠0,b>0)的解,则关于x的不等式k(x-4)+b>0的解集是.14. 不等式组 的解集是.15. 若不等式组 无解,化简 得 .16. 对于任意实数,m,n,定义一种运算: ,请根据上述定义解决问题:若关于x的不等式 的解集中只有一个整数解,则实数a的取值范围是.17. 某学校的编程课上,一位同学设计了一个运算程序,如图所示.按上述程序进行运算,程序运行到“判断结果是否大于23”为一次运行.若该程序只运行了2次就停止了,则x的取值范围是.
 18. 阅读下面的材料:对于实数 , ,我们定义符号 的意义为:当 时, ;当 时, ,如: , .根据上面的材料,当 时, 的取值范围 .
18. 阅读下面的材料:对于实数 , ,我们定义符号 的意义为:当 时, ;当 时, ,如: , .根据上面的材料,当 时, 的取值范围 .三、计算题
-
19. 解下列不等式或方程组(1)、(2)、20. 解下列不等式(组):(1)、 ;(2)、 .
四、解答题
-
21. 若关于x , y的方程组 的解,使不等式组 成立,求 的取值范围.22. 解不等式组: 并把解集在数轴上表示出来.
请结合题意填空,完成本题得解答①,
(1)、解不等式①,得(2)、解不等式②,得(3)、把不等式①和②的解集在数轴上表示: (4)、所以不等式得解集为 .23.(1)、解关于x的不等式 ,并求出其最大整数解;(2)、解关于x的不等式组24. 定义新运算“*”:对于任意有理数a,b,都有 ,(1)、已知 ,求 的值;(2)、若 的值大于10且小于16,求满足条件的 的整数值.25. 规定 的运算法则是 =ad-bc,例如 =2×5-3×1=7(1)、计算(2)、若 <-2,求x的取值范围。26.(1)、解不等式组 ,并把解集在数轴上表示出来.(2)、阅读某同学解分式方程的具体过程,回答后面问题:
(4)、所以不等式得解集为 .23.(1)、解关于x的不等式 ,并求出其最大整数解;(2)、解关于x的不等式组24. 定义新运算“*”:对于任意有理数a,b,都有 ,(1)、已知 ,求 的值;(2)、若 的值大于10且小于16,求满足条件的 的整数值.25. 规定 的运算法则是 =ad-bc,例如 =2×5-3×1=7(1)、计算(2)、若 <-2,求x的取值范围。26.(1)、解不等式组 ,并把解集在数轴上表示出来.(2)、阅读某同学解分式方程的具体过程,回答后面问题:解方程
解:原方程可化为: ①
②
③
④
检验:当 时,各分母均不为0,∴ 是原方程的解.
请回答:
①第②步变形的依据是 ▲ ;
②从第 ▲ 步开始出现了不符合题意,这一步错误的原因是 ▲ ;
③写出正确的求解过程.
27. 已知关于x,y的二元一次方程组(1)、若方程组的解 x,y的值互为相反数,求k的值;(2)、若方程组的解x,y的值满足x<1,且 ,求k的取值范围.28. 对非负数x“四舍五入”到个位的值记为〈x〉,即当n为非负整数时,若n﹣0.5≤x<n+0.5,则〈x〉=n.反之,当n为非负整数时,若〈x〉=n,则n﹣0.5≤x<n+0.5.如〈1.34〉=1,〈4.86〉=5.(1)、〈π〉=;(2)、若〈0.5x﹣1〉=7,则实数x的取值范围是 ;(3)、若关于x的不等式组 的整数解恰有4个,求a的取值范围;(4)、满足〈x〉= x的所有非负数x的值为 .