广东省东莞市2020-2021学年高一下学期数学期末考试试卷
试卷更新日期:2021-08-26 类型:期末考试
一、单选题
-
1. 设复数 满足 ,其中 为虚数单位,则复数 对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 已知向量 , 共线,则 的值为( )A、-1 B、0 C、1 D、23. 如图是水平放置的△ 的斜二测直观图△ , 是 的中点,则△ 中长度最长的线段为( )
 A、 B、 C、 D、4. 已知一组数据为85,87,88,90,92,则这组数据的第60百分位数为( )A、87 B、87.5 C、89 D、915. 已知圆柱的底面半径为1,母线长为2,则该圆柱的外接球的体积为( )A、 B、 C、 D、6. “大美中国古建筑名塔”榴花塔以红石为基,用青砖灰沙砌筑建成.如图,记榴花塔高为 ,测量小组选取与塔底 在同一水平面内的两个测量点 和 ,现测得 , , ,在点 处测得塔顶 的仰角为30°,则塔高 为( )
A、 B、 C、 D、4. 已知一组数据为85,87,88,90,92,则这组数据的第60百分位数为( )A、87 B、87.5 C、89 D、915. 已知圆柱的底面半径为1,母线长为2,则该圆柱的外接球的体积为( )A、 B、 C、 D、6. “大美中国古建筑名塔”榴花塔以红石为基,用青砖灰沙砌筑建成.如图,记榴花塔高为 ,测量小组选取与塔底 在同一水平面内的两个测量点 和 ,现测得 , , ,在点 处测得塔顶 的仰角为30°,则塔高 为( ) A、 B、 C、 D、7. 2021年3月,树人中学组织三个年级的学生进行“庆祝中国共产党成立100周年”党史知识竞赛.经统计,得到前200名学生分布的饼状图(如图)和前200名中高一学生排名分布的频率条形图(如图),则下列命题错误的是( )
A、 B、 C、 D、7. 2021年3月,树人中学组织三个年级的学生进行“庆祝中国共产党成立100周年”党史知识竞赛.经统计,得到前200名学生分布的饼状图(如图)和前200名中高一学生排名分布的频率条形图(如图),则下列命题错误的是( ) A、成绩前200名的200人中,高一人数比高二人数多30人 B、成绩第1-100名的100人中,高一人数不超过一半 C、成绩第1-50名的50人中,高三最多有32人 D、成绩第51-100名的50人中,高二人数比高一的多8. 在四边形 中, , , , ,则 的长为( )A、 B、 C、 D、
A、成绩前200名的200人中,高一人数比高二人数多30人 B、成绩第1-100名的100人中,高一人数不超过一半 C、成绩第1-50名的50人中,高三最多有32人 D、成绩第51-100名的50人中,高二人数比高一的多8. 在四边形 中, , , , ,则 的长为( )A、 B、 C、 D、二、多选题
-
9. 袋子中有1个红球,1个黄球,1个蓝球,从中取两个球,每次取一个球,取球后不放回,设事件 {第一个球是红球}, {第二个球是黄球},则下列结论正确的是( )A、 与 互为对立事件 B、 与 互斥 C、 D、10. 已知复数 , 是 的共轭复数,则下列结论正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则11. 已知 与 均为单位向量,其夹角为 ,则下列结论正确的是( )A、 B、 C、 D、12. 如图,在正方体 中, , , 分别为棱 , , 的中点,则下列结论正确的是( )
 A、 平面 B、点 与点 到平面 的距离相等 C、平面 截正方体 所得截面图形为等腰梯形 D、平面 将正方体 分割成的上、下两部分的体积之比为
A、 平面 B、点 与点 到平面 的距离相等 C、平面 截正方体 所得截面图形为等腰梯形 D、平面 将正方体 分割成的上、下两部分的体积之比为三、填空题
-
13. 如图,由A , 两个元件组成一个串联电路,元件A , 正常工作的概率分别为0.9和0.8,则电路正常工作的概率为.
 14. 广场上的玩具石凳是由正方体截去八个一样大的四面体得到的(如图).如果被截正方体的棱长为 ,那么玩具石凳的表面积为.
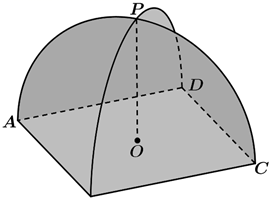
14. 广场上的玩具石凳是由正方体截去八个一样大的四面体得到的(如图).如果被截正方体的棱长为 ,那么玩具石凳的表面积为. 15. 已知点 , , 为坐标平面内一点,且 ,则满足条件的点 的一个坐标为.16. “牟和方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体,它是由两个相同的圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体(如图).如图所示的“四脚帐篷”类似于“牟和方盖”的一部分,其中 与 为相互垂直且全等的半圆面,它们的圆心为 ,半径为1.用平行于底面 的平面 去截“四脚帐篷”所得的截面图形为;当平面 经过 的中点时,截面图形的面积为.
15. 已知点 , , 为坐标平面内一点,且 ,则满足条件的点 的一个坐标为.16. “牟和方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体,它是由两个相同的圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体(如图).如图所示的“四脚帐篷”类似于“牟和方盖”的一部分,其中 与 为相互垂直且全等的半圆面,它们的圆心为 ,半径为1.用平行于底面 的平面 去截“四脚帐篷”所得的截面图形为;当平面 经过 的中点时,截面图形的面积为.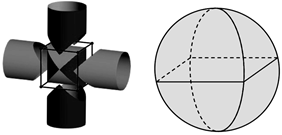
四、解答题
-
17. 设复数 i, i,记复数 与 分别对应复平面内的点 和 .(1)、根据复数及其运算的几何意义,求 和 两点间的距离;(2)、已知 ( 为正实数)表示动点 的集合是以点 为圆心, 为半径的圆.那么满足条件 的点 的集合是什么图形?并求出该图形的面积.18. 在△ 中,角 , , 所对的边分别为 , , .现有下列四个条件:① ,② ,③ ,④ .(1)、③④两个条件可以同时成立吗?请说明理由;(2)、请在上述四个条件中选择使△ 有解的三个条件,并求出△ 的面积.19. 如图,四棱锥 中, 为正方形, 为 中点,平面 平面 , , .
 (1)、证明: 平面 ;(2)、证明: ;(3)、求三棱锥 的体积.20. 如图,斜坐标系 中, , 分别是与 轴、 轴正方向同向的单位向量,且 , 的夹角为120°,定义向量 在斜坐标系 中的坐标为有序数对 ,在斜坐标系 中完成下列问题:
(1)、证明: 平面 ;(2)、证明: ;(3)、求三棱锥 的体积.20. 如图,斜坐标系 中, , 分别是与 轴、 轴正方向同向的单位向量,且 , 的夹角为120°,定义向量 在斜坐标系 中的坐标为有序数对 ,在斜坐标系 中完成下列问题: (1)、若向量 的坐标为(2,3),计算 的大小;(2)、若向量 的坐标为 ,向量 的坐标为 ,判断下列两个命题的真假,并说明理由.
(1)、若向量 的坐标为(2,3),计算 的大小;(2)、若向量 的坐标为 ,向量 的坐标为 ,判断下列两个命题的真假,并说明理由.命题①:若 ,则 ;命题②:若 ,则 .
21. 4月23日是世界读书日,树人中学为了解本校学生课外阅读情况,按性别进行分层,用分层随机抽样的方法从全校学生中抽出一个容量为100的样本,其中男生40名,女生60名.经调查统计,分别得到40名男生一周课外阅读时间(单位:小时)的频数分布表和60名女生一周课外阅读时间(单位:小时)的频率分布直方图:(以各组的区间中点值代表该组的各个值)男生一周阅读时间频数分布表
小时
频数
9
25
3
3
 (1)、从一周课外阅读时间为 的学生中按比例分配抽取6人,从这6人中任意抽取2人,求恰好一男一女的概率;(2)、分别估计男生和女生一周课外阅读时间的平均数 , ;(3)、估计总样本的平均数 和方差 .
(1)、从一周课外阅读时间为 的学生中按比例分配抽取6人,从这6人中任意抽取2人,求恰好一男一女的概率;(2)、分别估计男生和女生一周课外阅读时间的平均数 , ;(3)、估计总样本的平均数 和方差 .参考数据和公式:男生和女生一周课外阅读时间方差的估计值分别为 和 . , 和 分别表示男生和女生一周阅读时间的样本,其中 .
22. 如图,“雪糕筒”为校园中常见的交通标识,其可以近似的看成一个圆锥,如图,放置在水平地面上的某型号“雪糕筒”底面直径 ,母线 ,该“雪糕筒”绕点 被放倒后 、 、 在同一条直线上. (1)、求“雪糕筒”被放倒后最高点离水平地面的距离;(2)、求直线 与圆面 所成的角的余弦值;(3)、若放倒后的“雪糕筒”绕点 沿水平地面旋转一周,请说明旋转一周形成的曲面所围成的旋转体的特征(不用说明理由).
(1)、求“雪糕筒”被放倒后最高点离水平地面的距离;(2)、求直线 与圆面 所成的角的余弦值;(3)、若放倒后的“雪糕筒”绕点 沿水平地面旋转一周,请说明旋转一周形成的曲面所围成的旋转体的特征(不用说明理由).