湘教版数学九年级上册同步训练《第1章 反比例函数》单元检测B卷
试卷更新日期:2021-08-26 类型:单元试卷
一、单选题
-
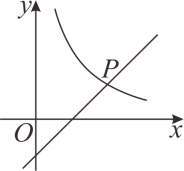
1. 已知反比例函数 ,则下列描述错误的是( )A、图象位于第一,第三象限 B、图象必经过点 C、图象不可能与坐标轴相交 D、 随 的增大而减小2. 已知反比例函数 ,当 时,y随x的增大而减小,那么一次的数 的图像经过第( )A、一,二,三象限 B、一,二,四象限 C、一,三,四象限 D、二,三,四象限3. 已知三个点(x1 , y1),(x2 , y2),(x3 , y3)在反比例函数y= 的图象上,其中x1<x2<0<x3 , 下列结论中正确的是( )A、y2<y1<0<y3 B、y1<y2<0<y3 C、y3<0<y2<y1 D、y3<0<y1<y24. 在平面直角坐标系 中,直线 垂直于 轴于点 (点 在原点的右侧),并分别与直线 和双曲线 相交于点 , ,且 ,则 的面积为( )A、 或 B、 或 C、 D、5. 如图,在平面直角坐标系中,函数 与 的图像交于点 ,则代数式 的值为( )
 A、 B、 C、 D、6. 已知正比例函数 和反比例函数 ,在同一直角坐标系下的图象如图所示,其中符合 的是( )
A、 B、 C、 D、6. 已知正比例函数 和反比例函数 ,在同一直角坐标系下的图象如图所示,其中符合 的是( ) A、①② B、①④ C、②③ D、③④7. 如图,点B在反比例函数 ( )的图象上,点C在反比例函数 ( )的图象上,且 轴, ,垂足为点C , 交y轴于点A , 则 的面积为 ( )
A、①② B、①④ C、②③ D、③④7. 如图,点B在反比例函数 ( )的图象上,点C在反比例函数 ( )的图象上,且 轴, ,垂足为点C , 交y轴于点A , 则 的面积为 ( )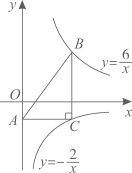 A、3 B、4 C、5 D、68. 如图,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO=AB,点C为斜边OB的中点,反比例函数y= (k>0,x>0)的图象过点C且交线段AB于点D,连接CD,OD,若S△OCD= ,则k的值为( )
A、3 B、4 C、5 D、68. 如图,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO=AB,点C为斜边OB的中点,反比例函数y= (k>0,x>0)的图象过点C且交线段AB于点D,连接CD,OD,若S△OCD= ,则k的值为( )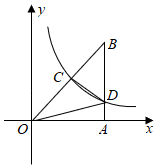 A、3 B、 C、2 D、19. 如图,点A是反比例函数 图象上的一点,过点A作 轴,垂足为点C , D为AC的中点,若 的面积为1,则k的值为( )
A、3 B、 C、2 D、19. 如图,点A是反比例函数 图象上的一点,过点A作 轴,垂足为点C , D为AC的中点,若 的面积为1,则k的值为( )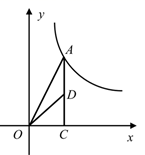 A、 B、 C、3 D、410. 已知反比例函数的图象经过点(2,﹣4),那么这个反比例函数的解析式是( )A、y= B、y=﹣ C、y= D、y=﹣11. 如图,平行于y轴的直线分别交 与 的图象(部分)于点A、B,点C是y轴上的动点,则 的面积为( )
A、 B、 C、3 D、410. 已知反比例函数的图象经过点(2,﹣4),那么这个反比例函数的解析式是( )A、y= B、y=﹣ C、y= D、y=﹣11. 如图,平行于y轴的直线分别交 与 的图象(部分)于点A、B,点C是y轴上的动点,则 的面积为( ) A、 B、 C、 D、12. 如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AE.若AD平分∠OAE,反比例函数y= (k>0,x>0)的图象经过AE上的两点A,F,且AF=EF,△ABE的面积为18,则k的值为( )
A、 B、 C、 D、12. 如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AE.若AD平分∠OAE,反比例函数y= (k>0,x>0)的图象经过AE上的两点A,F,且AF=EF,△ABE的面积为18,则k的值为( ) A、6 B、12 C、18 D、24
A、6 B、12 C、18 D、24二、填空题
-
13. 若反比例函数 的图象过点 ,则k的值等于.14. 在平面直角坐标系中,对于不在坐标轴上的任意一点 ,我们把点 称为点A的“倒数点”.如图,矩形 的顶点C为 ,顶点E在y轴上,函数 的图象与 交于点A.若点B是点A的“倒数点”,且点B在矩形 的一边上,则 的面积为.
 15. 如图,已知反比例函数过A , B两点,A点坐标 ,直线 经过原点,将线段 绕点B顺时针旋转90°得到线段 ,则C点坐标为 .
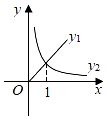
15. 如图,已知反比例函数过A , B两点,A点坐标 ,直线 经过原点,将线段 绕点B顺时针旋转90°得到线段 ,则C点坐标为 .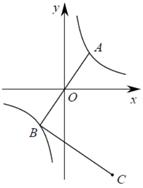 16. 已知:函数y1=|x|与函数y2= 的部分图象如图所示,有以下结论:
16. 已知:函数y1=|x|与函数y2= 的部分图象如图所示,有以下结论:①当x<0时,y1 , y2都随x的增大而增大;
②当x<﹣1时,y1>y2;
③y1与y2的图象的两个交点之间的距离是2;
④函数y=y1+y2的最小值是2.
则所有正确结论的序号是.
 17. 在平面直角坐标系 中,若反比例函数 的图象经过点 和点 ,则 的值为 .18. 如图,在平面直角坐标系中,正方形ABCD的顶点A在x轴正半轴上,顶点B,C在第一象限,顶点D的坐标 . 反比例函数 (常数 , )的图象恰好经过正方形ABCD的两个顶点,则k的值是.
17. 在平面直角坐标系 中,若反比例函数 的图象经过点 和点 ,则 的值为 .18. 如图,在平面直角坐标系中,正方形ABCD的顶点A在x轴正半轴上,顶点B,C在第一象限,顶点D的坐标 . 反比例函数 (常数 , )的图象恰好经过正方形ABCD的两个顶点,则k的值是.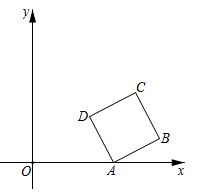
三、解答题
-
19. 如图所示,直线 与双曲线 交于A、B两点,已知点B的纵坐标为 ,直线AB与x轴交于点C , 与y轴交于点 , , .
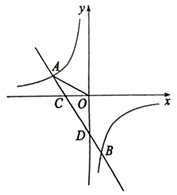 (1)、求直线AB的解析式;(2)、若点P是第二象限内反比例函数图象上的一点, 的面积是 的面积的2倍,求点P的坐标;(3)、直接写出不等式 的解集.20. 在直角坐标系中,设函数 ( 是常数, , )与函数 ( 是常数, )的图象交于点A,点A关于 轴的对称点为点B。
(1)、求直线AB的解析式;(2)、若点P是第二象限内反比例函数图象上的一点, 的面积是 的面积的2倍,求点P的坐标;(3)、直接写出不等式 的解集.20. 在直角坐标系中,设函数 ( 是常数, , )与函数 ( 是常数, )的图象交于点A,点A关于 轴的对称点为点B。 (1)、若点B的坐标为(-1,2),
(1)、若点B的坐标为(-1,2),①求 , 的值; ②当 时,直接写出 的取值范围;
(2)、若点B在函数 ( 是常数, )的图象上,求 的值。21. 如图, 中, ,边OB在x轴上,反比例函数 的图象经过斜边OA的中点M,与AB相交于点N, .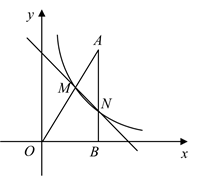 (1)、求k的值;(2)、求直线MN的解析式.22. 如图,在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象相交于点 ,与x轴相交于点B.
(1)、求k的值;(2)、求直线MN的解析式.22. 如图,在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象相交于点 ,与x轴相交于点B.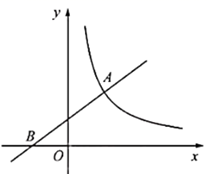 (1)、求反比例函数的表达式;(2)、过点A的直线交反比例函数的图象于另一点C,交x轴正半轴于点D,当 是以 为底的等腰三角形时,求直线 的函数表达式及点C的坐标.23. 如图,反比例函数的图象与过点 , 的直线交于点B和C.
(1)、求反比例函数的表达式;(2)、过点A的直线交反比例函数的图象于另一点C,交x轴正半轴于点D,当 是以 为底的等腰三角形时,求直线 的函数表达式及点C的坐标.23. 如图,反比例函数的图象与过点 , 的直线交于点B和C.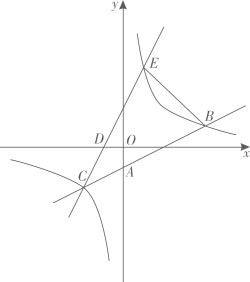 (1)、求直线AB和反比例函数的解析式.(2)、已知点 ,直线CD与反比例函数图象在第一象限的交点为E,直接写出点E的坐标,并求 的面积.24. 如图,已知反比例函数 与正比例函数 的图象交于 , 两点.
(1)、求直线AB和反比例函数的解析式.(2)、已知点 ,直线CD与反比例函数图象在第一象限的交点为E,直接写出点E的坐标,并求 的面积.24. 如图,已知反比例函数 与正比例函数 的图象交于 , 两点.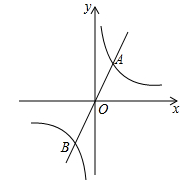 (1)、求该反比例函数的表达式;(2)、若点 在 轴上,且 的面积为3,求点 的坐标.25. 阅读下面的材料:
(1)、求该反比例函数的表达式;(2)、若点 在 轴上,且 的面积为3,求点 的坐标.25. 阅读下面的材料:如果函数 满足:对于自变量 取值范围内的任意 , ,
( 1 )若 ,都有 ,则称 是增函数;
( 2 )若 ,都有 ,则称 是减函数.
例题:证明函数 是增函数.
证明:任取 ,且 ,
则
∵ 且 ,
∴ ,
∴ ,即 ,
∴函数 是增函数.
根据以上材料解答下列问题:
(1)、函数 , , , , ;(2)、猜想 是函数 ▲ (填“增”或“减”),并证明你的猜想.