湘教版数学九年级上册同步训练《1.3 反比例函数的应用》
试卷更新日期:2021-08-26 类型:同步测试
一、单选题
-
1. 某气球内充满了一定质量 的气体,当温度不变时,气球内气体的气压 (单位: )是气体体积 (单位: )的反比例函数: ,能够反映两个变量 和 函数关系的图象是( )A、
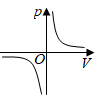 B、
B、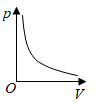 C、
C、 D、
D、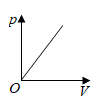 2. 已知蓄电池的电压为定值,使用蓄电池时,电流O(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
2. 已知蓄电池的电压为定值,使用蓄电池时,电流O(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( )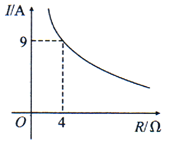 A、函数解析式为I= B、蓄电池的电压是18V C、当I≤10A时,R≥3.6Ω D、当R=6Ω时,I=4A3. 如图,平行四边形 的顶A在x轴的正半轴上,点 在对角线 上,反比例函数 的图像经过C、D两点.已知平行四边形 的面积是 ,则点B的坐标为( )
A、函数解析式为I= B、蓄电池的电压是18V C、当I≤10A时,R≥3.6Ω D、当R=6Ω时,I=4A3. 如图,平行四边形 的顶A在x轴的正半轴上,点 在对角线 上,反比例函数 的图像经过C、D两点.已知平行四边形 的面积是 ,则点B的坐标为( )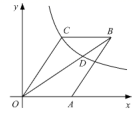 A、 B、 C、 D、4. 2019年10月,《长沙晚报》对外发布长沙高铁两站设计方案,该方案以三湘四水,杜鹃花开 ,塑造出杜鹃花开的美丽姿态,该高铁站建设初期需要运送大量的土石方,某运输公司承担了运送总量为 土石方的任务,该运输公司平均运送土石方的速度 (单位: 天)与完成运送任务所需的时间t(单位:天)之间的函数关系式是( )A、 B、 C、 D、5. 某公司计划新建一个容积V(m3)一定的长方体污水处理池,池的底面积S(m2)与其深度h(m)之间的函数关系式为 ,这个函数的图象大致是( )A、
A、 B、 C、 D、4. 2019年10月,《长沙晚报》对外发布长沙高铁两站设计方案,该方案以三湘四水,杜鹃花开 ,塑造出杜鹃花开的美丽姿态,该高铁站建设初期需要运送大量的土石方,某运输公司承担了运送总量为 土石方的任务,该运输公司平均运送土石方的速度 (单位: 天)与完成运送任务所需的时间t(单位:天)之间的函数关系式是( )A、 B、 C、 D、5. 某公司计划新建一个容积V(m3)一定的长方体污水处理池,池的底面积S(m2)与其深度h(m)之间的函数关系式为 ,这个函数的图象大致是( )A、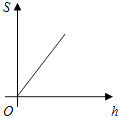 B、
B、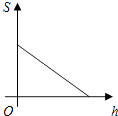 C、
C、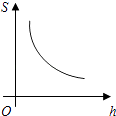 D、
D、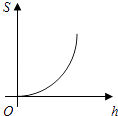 6. 如图,直线l1:x=1,l2:x=2,l3:x=3,l4:x=4,…,与函数y= (x>0)的图象分别交于点A1、A2、A3、A4、…;与函数y= 的图象分别交于点B1、B2、B3、B4、….如果四边形A1A2B2B1的面积记为S1 , 四边形A2A3B3B2的面积记为S2 , 四边形A3A4B4B3的面积记为S3 , …,以此类推.则S10的值是( )
6. 如图,直线l1:x=1,l2:x=2,l3:x=3,l4:x=4,…,与函数y= (x>0)的图象分别交于点A1、A2、A3、A4、…;与函数y= 的图象分别交于点B1、B2、B3、B4、….如果四边形A1A2B2B1的面积记为S1 , 四边形A2A3B3B2的面积记为S2 , 四边形A3A4B4B3的面积记为S3 , …,以此类推.则S10的值是( )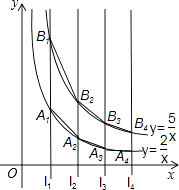 A、 B、 C、 D、7. 已知长方形的面积为20cm2 , 设该长方形一边长为ycm,另一边的长为xcm,则y与x之间的函数图象大致是( )A、
A、 B、 C、 D、7. 已知长方形的面积为20cm2 , 设该长方形一边长为ycm,另一边的长为xcm,则y与x之间的函数图象大致是( )A、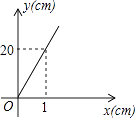 B、
B、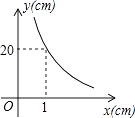 C、
C、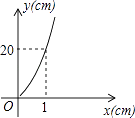 D、
D、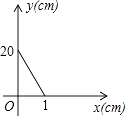 8. 函数 的图象是( )A、
8. 函数 的图象是( )A、 B、
B、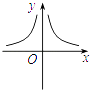 C、
C、 D、
D、 9. 在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也随之改变.密度ρ(单位:kg/m3)与体积V(单位:m3)满足函数关系式ρ= (k为常数,k≠0),其图象如图所示,则k的值为( )
9. 在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也随之改变.密度ρ(单位:kg/m3)与体积V(单位:m3)满足函数关系式ρ= (k为常数,k≠0),其图象如图所示,则k的值为( )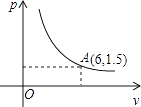 A、9 B、﹣9 C、4 D、﹣410. 如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数 (k<0)的图象在第二象限交于A(﹣3,m),B(n , 2)两点.若点E在x轴上,满足∠AEB=90°,且AE=2﹣m , 则k的值是( )
A、9 B、﹣9 C、4 D、﹣410. 如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数 (k<0)的图象在第二象限交于A(﹣3,m),B(n , 2)两点.若点E在x轴上,满足∠AEB=90°,且AE=2﹣m , 则k的值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图所示,双曲线 上有一动点A,连接 ,以O为顶点、 为直角边,构造等腰直角角形 ,则 面积的最小值为 . 此时A点坐标为 .
 12. 在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,当V=200时,p=50,则当p=25时,V= .13. 如图,在平面直角坐标系中,点A(a,4)为第一象限内一点,且a<4.连结OA,并以点A为旋转中心把OA逆时针转90°后得线段BA.若点A、B恰好都在同一反比例函数的图象上,则a的值等于.
12. 在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,当V=200时,p=50,则当p=25时,V= .13. 如图,在平面直角坐标系中,点A(a,4)为第一象限内一点,且a<4.连结OA,并以点A为旋转中心把OA逆时针转90°后得线段BA.若点A、B恰好都在同一反比例函数的图象上,则a的值等于. 14. 小宇每天骑自行车上学,从家到学校所需时间 (分)与骑车速度 (千米/分)关系如图所示.一天早上,由于起床晚了,为了不迟到,需不超过 分钟赶到学校,那么他骑车的速度至少是千米/分.
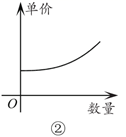
14. 小宇每天骑自行车上学,从家到学校所需时间 (分)与骑车速度 (千米/分)关系如图所示.一天早上,由于起床晚了,为了不迟到,需不超过 分钟赶到学校,那么他骑车的速度至少是千米/分. 15. 经济学家在硏究市场供求关系时,一般用纵轴表示产品单价(自变量),而用横轴表示产品数量(因变量),下列两条曲线分别表示某种产品数量与单价之间的供求关系,一条表示厂商希望的供应曲线,另一条表示客户希望的需求曲线,其中表示客户希望的需求曲线的是(填入序号即可).
15. 经济学家在硏究市场供求关系时,一般用纵轴表示产品单价(自变量),而用横轴表示产品数量(因变量),下列两条曲线分别表示某种产品数量与单价之间的供求关系,一条表示厂商希望的供应曲线,另一条表示客户希望的需求曲线,其中表示客户希望的需求曲线的是(填入序号即可).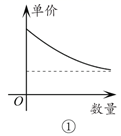
 16. 某中学要在校园内划出一块面积为100 m2的矩形土地做花圃,设这个矩形的相邻两边长分别为xm和ym,那么y关于x的函数解析式为.
16. 某中学要在校园内划出一块面积为100 m2的矩形土地做花圃,设这个矩形的相邻两边长分别为xm和ym,那么y关于x的函数解析式为.三、综合题
-
17. 电子体重科读数直观又便于携带,为人们带来了方便.某综合实践活动小组设计了简易电子体重秤:制作一个装有踏板(踏板质量忽略不计)的可变电阻R1 , R1与踏板上人的质量m之间的函数关系式为R1=km+b(其中k,b为常数,0≤m≤120),其图象如图1所示;图2的电路中,电源电压恒为8伏,定值电阻R0的阻值为30欧,接通开关,人站上踏板,电压表显示的读数为U0 , 该读数可以换算为人的质量m,
温馨提示:①导体两端的电压U,导体的电阻R,通过导体的电流I,满足关系式I= ;
②串联电路中电流处处相等,各电阻两端的电压之和等于总电压.
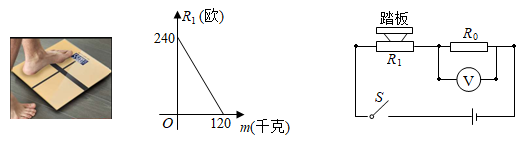 (1)、求k,b的值;(2)、求R1关于U0的函数解析式;(3)、用含U0的代数式表示m;(4)、若电压表量程为0~6伏,为保护电压表,请确定该电子体重秤可称的最大质量.18. 通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当 和 时,图象是线段;当 时,图象是反比例函数的一部分.
(1)、求k,b的值;(2)、求R1关于U0的函数解析式;(3)、用含U0的代数式表示m;(4)、若电压表量程为0~6伏,为保护电压表,请确定该电子体重秤可称的最大质量.18. 通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当 和 时,图象是线段;当 时,图象是反比例函数的一部分.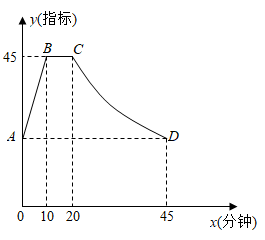 (1)、求点A对应的指标值;(2)、张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36?请说明理由.19. 为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要19min;完成2间办公室和1间教室的药物喷洒要11min.
(1)、求点A对应的指标值;(2)、张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36?请说明理由.19. 为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要19min;完成2间办公室和1间教室的药物喷洒要11min.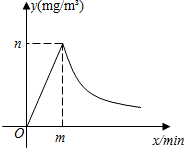 (1)、校医完成一间办公室和一间教室的药物喷洒各要多少时间?(2)、消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.20. 小明同学训练某种运算技能,每次训练完成相同数量的题目,各次训练题目难度相当. 当训练次数不超过15次时,完成一次训练所需要的时间y(单位:秒)与训练次数x(单位:次)之间满足如图所示的反比例函数关系. 完成第3次训练所需时间为400秒.
(1)、校医完成一间办公室和一间教室的药物喷洒各要多少时间?(2)、消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.20. 小明同学训练某种运算技能,每次训练完成相同数量的题目,各次训练题目难度相当. 当训练次数不超过15次时,完成一次训练所需要的时间y(单位:秒)与训练次数x(单位:次)之间满足如图所示的反比例函数关系. 完成第3次训练所需时间为400秒.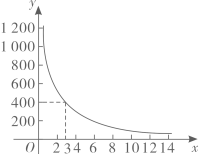 (1)、求y与x之间的函数关系式;(2)、当x的值为6,8,10时,对应的函数值分别为y1 , y2 , y3 , 比较(y1-y2)与(y2-y3)的大小: y1-y2y2-y3.21. 设函数y1= ,y2=- (k>0)。(1)、当2≤x≤3时,函数y1的最大值是a,函数y2的最小值是a-4,求a和k的值。(2)、设m≠0,且m≠-1,当x=m时,y1=p;当x=m+1时,y1=q。圆圆说:“p一定大于q”。你认为圆圆的说法正确吗?为什么?22. 如图,在平面直角坐标系中,A (6,0)、B(0, 4)是矩形OACB的两个顶点,双曲线 (k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线 的另一个交点,
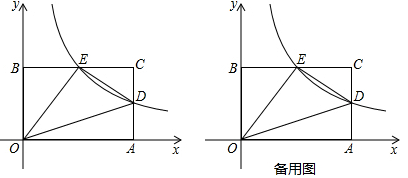
(1)、求y与x之间的函数关系式;(2)、当x的值为6,8,10时,对应的函数值分别为y1 , y2 , y3 , 比较(y1-y2)与(y2-y3)的大小: y1-y2y2-y3.21. 设函数y1= ,y2=- (k>0)。(1)、当2≤x≤3时,函数y1的最大值是a,函数y2的最小值是a-4,求a和k的值。(2)、设m≠0,且m≠-1,当x=m时,y1=p;当x=m+1时,y1=q。圆圆说:“p一定大于q”。你认为圆圆的说法正确吗?为什么?22. 如图,在平面直角坐标系中,A (6,0)、B(0, 4)是矩形OACB的两个顶点,双曲线 (k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线 的另一个交点,
 (1)、点D的坐标为 , 点E的坐标为.(2)、动点P在第一象限内,且满足 .
(1)、点D的坐标为 , 点E的坐标为.(2)、动点P在第一象限内,且满足 .①若点P在这个反比例函数的图象上,求点P的坐标;
②连接PO、PE,当PO-PE的值最大时,求点P的坐标;
③若点Q是平面内一点,使得以A、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.