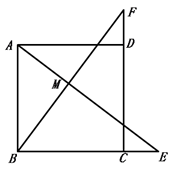北师版九年级数学《第一章 特殊平行四边形》单元检测A卷
试卷更新日期:2021-08-26 类型:单元试卷
一、单选题
-
1. 如图,在直角坐标系中,菱形 的顶点A , B , C在坐标轴上,若点B的坐标为 , ,则点D的坐标为( )
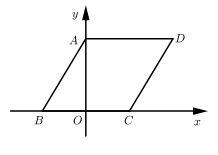 A、 B、 C、 D、2. 如图,四边形 是菱形,对角线 , 相交于点 , , ,点 是 上一动点,点 是 的中点,则 的最小值为( )
A、 B、 C、 D、2. 如图,四边形 是菱形,对角线 , 相交于点 , , ,点 是 上一动点,点 是 的中点,则 的最小值为( )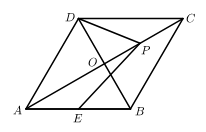 A、 B、 C、3 D、3. 如图,菱形 的对角线 、 相交于点 ,过点 作 于点 ,连接 ,若 , ,则菱形 的面积为( )
A、 B、 C、3 D、3. 如图,菱形 的对角线 、 相交于点 ,过点 作 于点 ,连接 ,若 , ,则菱形 的面积为( )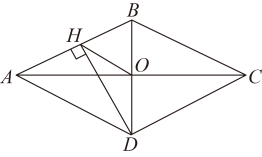 A、72 B、24 C、48 D、964. 如图,在矩形纸片ABCD中, , ,M是BC上的点,且 .将矩形纸片ABCD沿过点M的直线折叠,使点D落在AB上的点P处,点C落在点 处,折痕为MN,则线段PA的长是( )
A、72 B、24 C、48 D、964. 如图,在矩形纸片ABCD中, , ,M是BC上的点,且 .将矩形纸片ABCD沿过点M的直线折叠,使点D落在AB上的点P处,点C落在点 处,折痕为MN,则线段PA的长是( ) A、4 B、5 C、6 D、5. 如图,点 在矩形 的对角线 所在的直线上, ,则四边形 是( )
A、4 B、5 C、6 D、5. 如图,点 在矩形 的对角线 所在的直线上, ,则四边形 是( )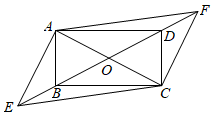 A、平行四边形 B、矩形 C、菱形 D、正方形6. 如图,将矩形纸片ABCD的两个直角进行折叠,使CB,AD恰好落在对角线AC上,B′,D′分别是B,D的对应点,折痕分别为CF,AE.若AB=4,BC=3,则线段 的长是( )
A、平行四边形 B、矩形 C、菱形 D、正方形6. 如图,将矩形纸片ABCD的两个直角进行折叠,使CB,AD恰好落在对角线AC上,B′,D′分别是B,D的对应点,折痕分别为CF,AE.若AB=4,BC=3,则线段 的长是( ) A、 B、2 C、 D、17. 如图,在平行四边形 中, , .连接AC , 过点B作 ,交DC的延长线于点E , 连接AE , 交BC于点F . 若 ,则四边形ABEC的面积为( )
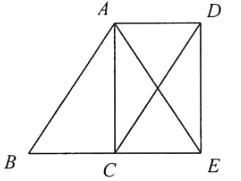
A、 B、2 C、 D、17. 如图,在平行四边形 中, , .连接AC , 过点B作 ,交DC的延长线于点E , 连接AE , 交BC于点F . 若 ,则四边形ABEC的面积为( )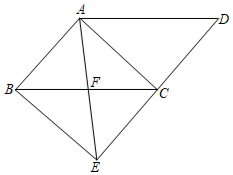 A、 B、 C、6 D、8. 如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设 ,则 为( )
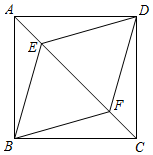
A、 B、 C、6 D、8. 如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设 ,则 为( )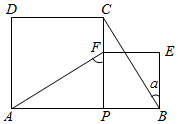 A、2α B、90°﹣α C、45°+α D、90°﹣ α9. 已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )A、选①② B、选选①③ C、选②③ D、选②④10. 如图,已知F、E分别是正方形 的边 与 的中点, 与 交于P.则下列结论成立的是( )
A、2α B、90°﹣α C、45°+α D、90°﹣ α9. 已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )A、选①② B、选选①③ C、选②③ D、选②④10. 如图,已知F、E分别是正方形 的边 与 的中点, 与 交于P.则下列结论成立的是( )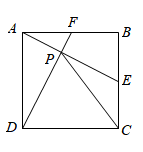 A、 B、 C、 D、11. 下列命题是真命题的是( )A、对角线相等的四边形是平行四边形 B、对角线互相平分且相等的四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直平分的四边形是正方形12. 如图,在正方形 中, ,E为对角线 上与A,C不重合的一个动点,过点E作 于点F, 于点G,连接 .下列结论:
A、 B、 C、 D、11. 下列命题是真命题的是( )A、对角线相等的四边形是平行四边形 B、对角线互相平分且相等的四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直平分的四边形是正方形12. 如图,在正方形 中, ,E为对角线 上与A,C不重合的一个动点,过点E作 于点F, 于点G,连接 .下列结论: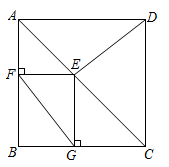
① ;② ;③ ;④ 的最小值为3.其中正确结论的个数有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 如图,BD是菱形ABCD的一条对角线,点E在BC的延长线上,若 ,则 的度数为度.
 14. 如图,在菱形ABCD中, , ,Q为AB的中点,P为对角线BD上的任意一点,则 的最小值为.
14. 如图,在菱形ABCD中, , ,Q为AB的中点,P为对角线BD上的任意一点,则 的最小值为. 15. 如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连结DF,EF。若MF=AB,则∠DAF=度。
15. 如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连结DF,EF。若MF=AB,则∠DAF=度。 16. 如图,在平行四边形 中,对角线 、 相交于点O,在不添加任何辅助线的情况下,请你添加一个条件 , 使平行四边形 是矩形.
16. 如图,在平行四边形 中,对角线 、 相交于点O,在不添加任何辅助线的情况下,请你添加一个条件 , 使平行四边形 是矩形.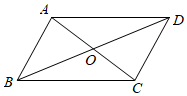 17. 如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°.
17. 如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°.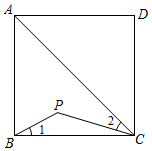 18. 如图,在矩形 中, , , 、 分别是边 、 上一点, ,将 沿 翻折得 ,连接 ,当 时, 是以 为腰的等腰三角形.
18. 如图,在矩形 中, , , 、 分别是边 、 上一点, ,将 沿 翻折得 ,连接 ,当 时, 是以 为腰的等腰三角形.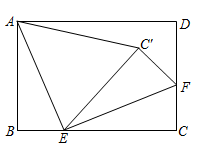
三、解答题
-
19. 如图,矩形 的对角线 , 交于点 ,且 , ,连接 .求证: .
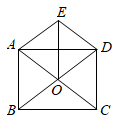 20. 如图,四边形 是菱形,点 、 分别在边 、 的延长线上,且 .连接 、 .
20. 如图,四边形 是菱形,点 、 分别在边 、 的延长线上,且 .连接 、 .求证: .
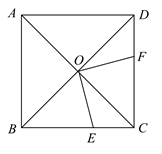
 21. 已知:如图,在正方形 中,对角线 相交于点O,点 分别是边 上的点,且 .
21. 已知:如图,在正方形 中,对角线 相交于点O,点 分别是边 上的点,且 .求证: .
 22. 如图,在正方形ABCD中,点E,F在AC上,且AF=CE.求证:四边形BEDF是菱形.
22. 如图,在正方形ABCD中,点E,F在AC上,且AF=CE.求证:四边形BEDF是菱形.