2022年苏科版初中数学《中考一轮复习》专题二方程与不等式 2.1 一元一次方程

试卷更新日期：2021-08-25 类型：一轮复习

进入出卷网下载

一、单选题

1. 已知下列方程：① $\frac{1}{3}$ x＝2；② $\frac{1}{x}$ ＝3；③ $\frac{x}{2}$ ＝2x－1；④2x²＝1；⑤2x＋y＝1.其中一元一次方程的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
2. 已知二元一次方程4x+5y＝5，用含x的代数式表示y ，则可表示为（）

A、y＝﹣ $\frac{4}{5}$ x+1 B、y＝﹣ $\frac{4}{5}$ x﹣1 C、y＝ $\frac{4}{5}$ x+1 D、y＝ $\frac{4}{5}$ x﹣1

查看试题解析
3. 若关于x的一元一次不等式组 ${\begin{matrix} 3 - 3 x < x - 5 \\ x - m > - 1 \end{matrix}$ 的解集为 $x > 2$ ，且关于x的方程 $\frac{2 x - m}{3} = 1$ 的解为非负整数，则符合条件的整数 $m$ 的个数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 已知某商店有两件进价不同的运动衫都卖了160元，其中一件盈利60%，另一件亏损20%，在这次买卖中这家商店（）

A、不盈不亏 B、盈利20元 C、盈利10元 D、亏损20元

查看试题解析
5. 用150张铁皮做罐头盒，每张铁皮可制盒身15个或盒底45个，1个盒身与2个盒底配成一套罐头盒，为使制成的盒身与盒底恰好配套，可设用x张铁皮制盒底，则（）

A、 $2 \times 15 x = 45 (150 - x)$ B、 $15 x = 2 \times 45 (150 - x)$ C、 $2 \times 15 (150 - x) = 45 x$ D、 $15 (150 - x) = 2 \times 45 x$

查看试题解析
6. 完成某项工程，甲单独做10天完成，乙单独做7天完成，现在由甲先做了3天，乙再参加合作，求完成这项工程总共用去的时间，若设完成此项工程总共用 $x$ 天，则下列方程中正确的是（）

A、 $\frac{x + 3}{10} + \frac{x}{7} = 1$ B、 $\frac{x + 3}{10} + \frac{x + 3}{7} = 1$ C、 $\frac{x}{10} + \frac{x}{7} = 1$ D、 $\frac{x}{10} + \frac{x - 3}{7} = 1$

查看试题解析
7. 一种长方形餐桌的四周可坐6人用餐，现把若干张这样的餐桌按如图所示的方式拼接.若用餐的人数有90人，则这样的餐桌需要（）

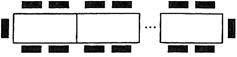A、15张 B、16张 C、21张 D、22张

查看试题解析
8. 有 $m$ 辆客车及 $n$ 个人，若每辆客车乘40人，则还有10人不能上车；若每辆客车乘43人，则只有1人不能上车，下列四个方程错误的是（）

A、 $40 m - 10 = 43 m - 1$ B、 $40 m + 10 = 43 m + 1$ C、 $43 (n - 10) = 40 (n - 1)$ D、 $\frac{n - 10}{40} = \frac{n - 1}{43}$

查看试题解析
9. 如图所示，正方形的边长为120 m，小明和小华都沿着正方形的边按逆时针方向跑步，二人同时起跑，小明从A点开始，速度是4 m/s，小华从C点开始，速度是5.5 m/s，小华第一次追上小明是在哪条边上（）

A、AB B、BC C、CD D、DA

查看试题解析
10. 某超市推出如下优惠方案：（1）一次性购物不超过100元不享受优惠；（2）一次性购物超过100元，但不超过300元一律九折；（3）一次性购物超过300元一律八折；兰兰两次购物分别付款80元，252元．如果兰兰一次性购买和上两次相同的物品应付款（）

A、288元 B、288元和332元 C、332元 D、288元和316元

查看试题解析

二、填空题

11. 若关于 $x$ 的方程 $(m - 2) x^{| m | - 1} = 5$ 是一元一次方程，则. $m =$ .

查看试题解析
12. 如果 $2 x + 3$ 的值与 $31 - x$ 的值互为相反数，那么 $x$ 等于.

查看试题解析
13. 规定“Φ“是一种新的运算符号：aΦb＝a²＋ab﹣1，已知3Φ（﹣2Φx）＝5，则x＝.

查看试题解析
14. 若关于 $x$ 的方程 $2 x + a = 4$ 的解在数轴上表示的点到原点的距离为 $3$ ，则 $a$ 的值为.

查看试题解析
15. 我国古代数学著作《算学启蒙》中有这样一个数学问题，其大意是：跑得快的马每天走240里，跑得慢的马每天走150里，慢马先走12天，快马几天可以追上慢马？设快马x天可以追上慢马，根据题意，可列方程为．

查看试题解析
16. 有一列数，按一定的规律排列成 $\frac{1}{3}$ ，-1，3，-9，27，-8181，….若其中某三个相邻数的和是-567，则这三个数中第一个数是.

查看试题解析
17. 如图， $A B = 20 cm$ ，点 $C$ 是线段 $A B$ 的中点，点 $P$ 从点 $A$ 出发，以 $2 cm/s$ 的速度向右移动，同时点 $Q$ 从点 $C$ 出发，以 $3cm/s$ 的速度向右移动到点 $B$ 后立即原速返回点 $A$ ，当点 $Q$ 到达点 $A$ 时， $P 、 Q$ 两点同时停止运动.当 $P Q = 12 cm$ 时，运动时间 $t$ 的值是.

查看试题解析
18. 小明和小慧两位同学在数学活动课中，把长为30cm、宽为10cm的长方形白纸条黏合起来，小明按如图1所示的方法黏合起来得到长方形ABCD，黏合部分的长度为6cm，小慧按如图2所示的方法黏合起来得到长方形A₁B₁C₁D₁ ，黏合部分的长度为4cm.若长为30cm、宽为10cm的长方形白纸条共有100张，则小明应分配到张长方形白纸条，才能使小明和小慧按各自要求黏合起来的长方形面积相等（要求100张长方形白纸条全部用完）.

查看试题解析

三、计算题

19. 解方程

(1)、5x+2=3（x+2）

(2)、 $\frac{2 x - 1}{4} = 1 - \frac{3 - x}{8}$ ．

查看试题解析
20. 解方程：

(1)、 $6 - 2 x = 3 x - 4$ ；

(2)、 $\frac{3}{2} [2 （ x - \frac{2}{3}) + \frac{4}{3}] = 1$

查看试题解析

四、解答题

21. 已知关于x的方程 $2 (x + 1) - m = - \frac{m - 2}{2}$ 的解比方程 $5 (x - 1) - 1 = 4 (x - 1) + 1$ 的解大2．求m值．

查看试题解析
22. 已知关于 $x$ 、 $y$ 的方程组 ${\begin{array}{l} x - 2 y = - 3 - a \\ x + y = 3 + 2 a \end{array}$ 的解也是二元一次方程 $2 x + 3 y = 18$ 的解，求 $a$ 的值.

查看试题解析
23. 大学生运动会将在成都召开，大批的大学生报名参与志愿者服务工作.某大学计划组织本校大学生志愿者乘车去了解比赛场馆情况，若单独调配36座（不含司机）新能源客车若干辆，则有2人没有座位；若只调配22座（不含司机）新能源客车，则用车数量将增加4辆，并空出2个座位.求计划调配36座新能源客车多少辆？该大学共有多少名大学生志愿者？

查看试题解析
24. 为了美化环境，建设生态桂林，某社区需要进行绿化改造，现有甲、乙两个绿化工程队可供选择，已知甲队每天能完成的绿化改造面积比乙队多200平方米，甲队与乙队合作一天能完成800平方米的绿化改造面积.

(1)、甲、乙两工程队每天各能完成多少平方米的绿化改造面积？

(2)、该社区需要进行绿化改造的区域共有12000平方米，甲队每天的施工费用为600元，乙队每天的施工费用为400元，比较以下三种方案：①甲队单独完成；②乙队单独完成；③甲、乙两队全程合作完成.哪一种方案的施工费用最少？

查看试题解析
25. 一辆卡车从甲地匀速开往乙地，出发2小时后，一辆轿车从甲地去追这辆卡车，轿车的速度比卡车的速度每小时快30千米，但轿车行驶一小时后突遇故障修理15分钟后，又上路追这辆卡车，但速度减小了 $\frac{1}{3}$ ，结果又用两小时才追上这辆卡车，求卡车的速度．

查看试题解析
26. 甲、乙两家超市以相同的价格出售同样的商品.为了吸引顾客，各自推出不同的优惠方案：在甲超市累计购买商品超出 $300$ 元之后，超出部分按原价八折优惠；在乙超市累计购买商品超出 $200$ 元之后，超出部分按原价九折优惠.设顾客预计累计购物x元 $(x > 300)$ ，试比较顾客到哪家超市购物更优惠？说明你的理由.

查看试题解析
27. 南宁市某体育器材经营店销售A型，B型两种品牌立定跳远考试测试仪，今年两种型号的测试仪的进价和售价如下表．已知A型测试仪去年和今年的1月份销售总额分别为4万元，6万元，今年A型测试仪每台销售价比去年增加400元．今年1月份A型测试仪的销售数量与去年1月份相同．

立定跳远测试仪

A型

B型

进价（元/台）

1000

1100

售价（元/台）

x

1500

(1)、求今年1月份的A型立定跳远测试仪的销售单价.（用列方程的方法解答）

(2)、进入3月份，各校进入体育中考备考冲刺阶段，立定跳远测试仪销量大增，该店计划3月份再进一批A型和B型立定跳远考试测试仪共200台，且B型测试仪不超过A型测试仪的2倍，设A型立定跳远测试仪售价为x元/台，应如何进货才能使这批测试仪获利最多？

(3)、该体育器材经营店为了吸引客源，增加销量，准备增购一种进价为500元/台的C型立定跳远测试仪，购进这三种立定跳远测试仪若干台共用8万元，其中B型的数量是A型数量的2倍，设A型测试仪购进a台，则该店至少可以购进三种测试仪共多少台？

查看试题解析
28. 已知在数轴上有A，B两点，点B表示的数为最大的负整数，点A在点B的右边，且AB=24.若有一动点Р从数轴上点A出发，以每秒2个单位长度的速度沿数轴向左匀速运动，动点Q从点B出发，以每秒3个单位长度的速度沿着数轴向右匀速运动，设Q运动时间为t秒.

(1)、若点Р和点Q同时出发，当 $t = 2$ 秒时，写出数轴上点P，Q所表示的数；

(2)、若点P，Q分别从A，B两点出发，Р先出发2秒，然后Q才出发，问当t为何值点P与点相距3个单位长度；

(3)、若点О到点M，N两点的距离之和为10，则称点О是 $[M ， N]$ 的“整十点”，设点C为线段AB上的点，且 $A C = 10$ ，点P，Q分别从A，B两点同时出发，点P向左运动到C点时返回到A点时停止，动点Q一直向右运动到A点后停止运动，求当t为何值时，点C为 $[P ， Q]$ 的“整十点”.

查看试题解析

立定跳远测试仪	A型	B型
进价（元/台）	1000	1100
售价（元/台）	x	1500

2022年苏科版初中数学《中考一轮复习》专题二 方程与不等式 2.1 一元一次方程

一、单选题

二、填空题

三、计算题

四、解答题

2022年苏科版初中数学《中考一轮复习》专题二方程与不等式 2.1 一元一次方程