广东省中考数学真题汇编(近三年) 专题8 图形的变换
试卷更新日期:2021-08-25 类型:二轮复习
一、单选题
-
1. 下列四个银行标志中,既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形中是轴对称图形的是( )A、
2. 下列图形中是轴对称图形的是( )A、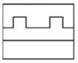 B、
B、 C、
C、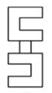 D、
D、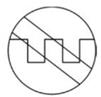 3. 如图,由4个相同正方体组合而成的几何体,它的左视图是( )
3. 如图,由4个相同正方体组合而成的几何体,它的左视图是( )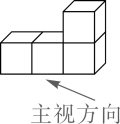 A、
A、 B、
B、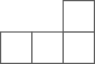 C、
C、 D、
D、 4. 如图,在 中, , , ,将 绕点A逆时针旋转得到 ,使点 落在AB边上,连结 ,则 的值为( )
4. 如图,在 中, , , ,将 绕点A逆时针旋转得到 ,使点 落在AB边上,连结 ,则 的值为( ) A、 B、 C、 D、5. 如图,在点F处,看建筑物顶端D的仰角为32°,向前走了15米到达点E即 米,在点E处看点D的仰角为64°,则 的长用三角函数表示为( )
A、 B、 C、 D、5. 如图,在点F处,看建筑物顶端D的仰角为32°,向前走了15米到达点E即 米,在点E处看点D的仰角为64°,则 的长用三角函数表示为( )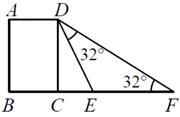 A、 B、 C、 D、6. 下列图形中既是轴对称图形,也是中心对称图形的是( )A、
A、 B、 C、 D、6. 下列图形中既是轴对称图形,也是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )
7. 如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )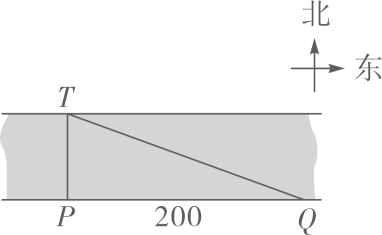 A、200tan70°米 B、 米 C、200sin70°米 D、 米8. 下列哪个图形,主视图、左视图和俯视图相同的是( )
A、200tan70°米 B、 米 C、200sin70°米 D、 米8. 下列哪个图形,主视图、左视图和俯视图相同的是( )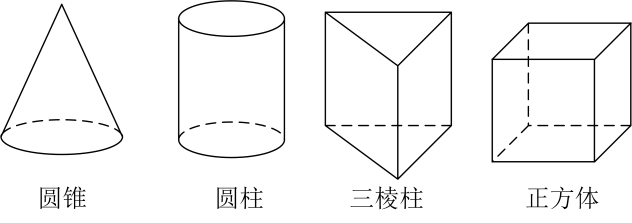 A、圆锥 B、圆柱 C、三棱柱 D、正方体9. 如图所示的圆锥,下列说法正确的是( )
A、圆锥 B、圆柱 C、三棱柱 D、正方体9. 如图所示的圆锥,下列说法正确的是( )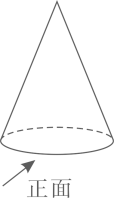 A、该圆锥的主视图是轴对称图形 B、该圆锥的主视图是中心对称图形 C、该圆锥的主视图既是轴对称图形,又是中心对称图形 D、该圆锥的主视图既不是轴对称图形,又不是中心对称图形10. 如图, 中, , , ,以点 为圆心, 为半径作 ,当 时, 与 的位置关系是( )
A、该圆锥的主视图是轴对称图形 B、该圆锥的主视图是中心对称图形 C、该圆锥的主视图既是轴对称图形,又是中心对称图形 D、该圆锥的主视图既不是轴对称图形,又不是中心对称图形10. 如图, 中, , , ,以点 为圆心, 为半径作 ,当 时, 与 的位置关系是( ) A、相离 B、相切 C、相交 D、无法确定11. 在平面直角坐标系中,点 关于 轴对称的点的坐标为( )A、 B、 C、 D、12. 如图,在正方形 中, ,点 , 分别在边 , 上, .若将四边形 沿 折叠,点 恰好落在 边上,则 的长度为( )
A、相离 B、相切 C、相交 D、无法确定11. 在平面直角坐标系中,点 关于 轴对称的点的坐标为( )A、 B、 C、 D、12. 如图,在正方形 中, ,点 , 分别在边 , 上, .若将四边形 沿 折叠,点 恰好落在 边上,则 的长度为( ) A、1 B、 C、 D、213. 如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若 ,则次斜坡的水平距离AC为( )
A、1 B、 C、 D、213. 如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若 ,则次斜坡的水平距离AC为( )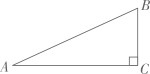 A、75m B、50m C、30m D、12m14. 如图,平行四边形ABCD中,AB=2,AD=4,对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点,则下列说法正确的是( )
A、75m B、50m C、30m D、12m14. 如图,平行四边形ABCD中,AB=2,AD=4,对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点,则下列说法正确的是( )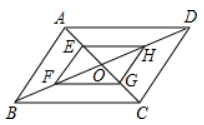 A、EH=HG B、四边形EFGH是平行四边形 C、AC⊥BD D、 的面积是 的面积的2倍15. 已知菱形ABCD,E、F是动点,边长为4,BE=AF,∠BAD=120°,则下列结论:
A、EH=HG B、四边形EFGH是平行四边形 C、AC⊥BD D、 的面积是 的面积的2倍15. 已知菱形ABCD,E、F是动点,边长为4,BE=AF,∠BAD=120°,则下列结论: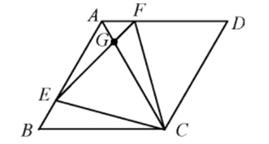
①△BCE≌△ACF②△CEF为正三角形③∠AGE=∠BEC④若AF=1,则EG=3FG正确的有( )个.
A、1 B、2 C、3 D、416. 在平面直角坐标系xOy中,矩形OABC的点A在函数 的图象上,点C在函数 的图象上,若点B的横坐标为 ,则点A的坐标为( )A、 B、 C、 D、17. 如图,矩形 的对角线 , 交于点 , , ,过点 作 ,交 于点 ,过点 作 ,垂足为 ,则 的值为( ) A、 B、 C、 D、18. 如图,正方形 的边长为4,延长 至 使 ,以 为边在上方作正方形 ,延长 交 于 ,连接 、 , 为 的中点,连接 分别与 、 交于点 、 .则下列结论:① ;② ;③ ;④ .其中符合题意的结论有( )
A、 B、 C、 D、18. 如图,正方形 的边长为4,延长 至 使 ,以 为边在上方作正方形 ,延长 交 于 ,连接 、 , 为 的中点,连接 分别与 、 交于点 、 .则下列结论:① ;② ;③ ;④ .其中符合题意的结论有( )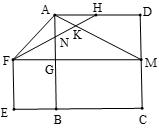 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
19. 如图,在 中, .过点D作 ,垂足为E , 则 .
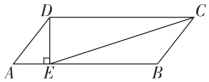 20. 如图,已知四边形ABCD,AC与BD相交于点O,∠ABC=∠DAC=90°, ,则 = .
20. 如图,已知四边形ABCD,AC与BD相交于点O,∠ABC=∠DAC=90°, ,则 = .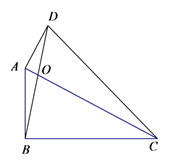 21. 如图,点 的坐标为 ,点 在 轴上,把 沿 轴向右平移到 ,若四边形 的面积为9,则点 的坐标为 .
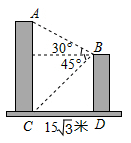
21. 如图,点 的坐标为 ,点 在 轴上,把 沿 轴向右平移到 ,若四边形 的面积为9,则点 的坐标为 .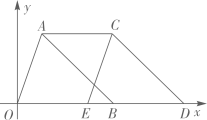 22. 如图,某校教学楼 与实验楼 的水平间距 米,在实验楼顶部 点测得教学楼顶部 点的仰角是 ,底部 点的俯角是 ,则教学楼 的高度是米(结果保留根号).
22. 如图,某校教学楼 与实验楼 的水平间距 米,在实验楼顶部 点测得教学楼顶部 点的仰角是 ,底部 点的俯角是 ,则教学楼 的高度是米(结果保留根号).
 23. 一副三角板如图放置,将三角板ADE绕点A逆时针旋转 ,使得三角板ADE的一边所在的直线与BC垂直,则 的度数为.
23. 一副三角板如图放置,将三角板ADE绕点A逆时针旋转 ,使得三角板ADE的一边所在的直线与BC垂直,则 的度数为.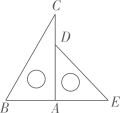 24. 如图,正方形 中, 绕点 逆时针旋转到 , , 分别交对角线 于点 ,若 ,则 的值为 .
24. 如图,正方形 中, 绕点 逆时针旋转到 , , 分别交对角线 于点 ,若 ,则 的值为 .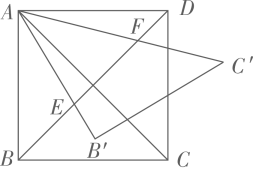
三、计算题
-
25. 计算: -2cos60°+( )-1+(π-3.14)0 .26. 计算: .
四、解答题
-
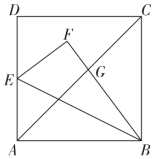
27. 如图,边长为1的正方形 中,点E为 的中点.连接 ,将 沿 折叠得到 交 于点G , 求 的长.
 28. 如图所示,某施工队要测量隧道BC长度,已知:AD=600米,AD⊥BC,施工队站在点D处看向B,测得仰角为45°,再由D走到E处测量,DE∥AC,ED=500米,测得仰角为53°,求隧道BC长.(sin53°≈ ,cos53°≈ ,tan53°≈ ).
28. 如图所示,某施工队要测量隧道BC长度,已知:AD=600米,AD⊥BC,施工队站在点D处看向B,测得仰角为45°,再由D走到E处测量,DE∥AC,ED=500米,测得仰角为53°,求隧道BC长.(sin53°≈ ,cos53°≈ ,tan53°≈ ).
五、综合题
-
29. 如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(-1,2),AB⊥x轴于点E,正比例函数y=mx的图像与反比例函数 的图像相交于A,P两点。
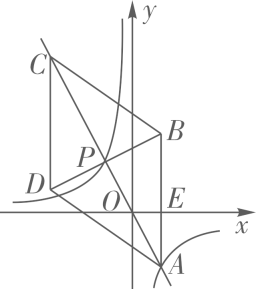 (1)、求m,n的值与点A的坐标;(2)、求证: ∽(3)、求 的值30. 如图,抛物线 与 轴交于 , 两点,点 , 分别位于原点的左、右两侧, ,过点 的直线与 轴正半轴和抛物线的交点分别为 , , .
(1)、求m,n的值与点A的坐标;(2)、求证: ∽(3)、求 的值30. 如图,抛物线 与 轴交于 , 两点,点 , 分别位于原点的左、右两侧, ,过点 的直线与 轴正半轴和抛物线的交点分别为 , , . (1)、求 , 的值;(2)、求直线 的函数解析式;(3)、点 在抛物线的对称轴上且在 轴下方,点 在射线 上,当 与 相似时,请直接写出所有满足条件的点 的坐标.31. 如图,在 中, ,作 的垂直平分线交 于点D , 延长 至点E , 使 .
(1)、求 , 的值;(2)、求直线 的函数解析式;(3)、点 在抛物线的对称轴上且在 轴下方,点 在射线 上,当 与 相似时,请直接写出所有满足条件的点 的坐标.31. 如图,在 中, ,作 的垂直平分线交 于点D , 延长 至点E , 使 . (1)、若 ,求 的周长;(2)、若 ,求 的值.32. 在平面直角坐标系 中,一次函数 的图象与x轴、y轴分别交于A、B两点,且与反比例函数 图象的一个交点为 .(1)、求m的值;(2)、若 ,求k的值.33. 探究:是否存在一个新矩形,使其周长和面积为原矩形的2倍、 倍、k倍.(1)、若该矩形为正方形,是否存在一个正方形,使其周长和面积都为边长为2的正方形的2倍?(填“存在”或“不存在”).(2)、继续探究,是否存在一个矩形,使其周长和面积都为长为3,宽为2的矩形的2倍?
(1)、若 ,求 的周长;(2)、若 ,求 的值.32. 在平面直角坐标系 中,一次函数 的图象与x轴、y轴分别交于A、B两点,且与反比例函数 图象的一个交点为 .(1)、求m的值;(2)、若 ,求k的值.33. 探究:是否存在一个新矩形,使其周长和面积为原矩形的2倍、 倍、k倍.(1)、若该矩形为正方形,是否存在一个正方形,使其周长和面积都为边长为2的正方形的2倍?(填“存在”或“不存在”).(2)、继续探究,是否存在一个矩形,使其周长和面积都为长为3,宽为2的矩形的2倍?同学们有以下思路:
①设新矩形长和宽为x、y , 则依题意 , ,
联立 得 ,再探究根的情况:
根据此方法,请你探究是否存在一个矩形,使其周长和面积都为原矩形的 倍;
②如图也可用反比例函数与一次函数证明 : , : ,那么,
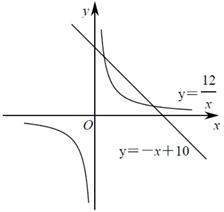
a . 是否存在一个新矩形为原矩形周长和面积的2倍?
b . 请探究是否有一新矩形周长和面积为原矩形的 ,若存在,用图像表达;
c . 请直接写出当结论成立时k的取值范围:.
34. 背景:一次小组合作探究课上,小明将两个正方形按背景图位置摆放(点E,A,D在同一条直线上),发现BE=DG且BE⊥DG.小组讨论后,提出了三个问题,请你帮助解答: (1)、将正方形AEFG绕点A按逆时针方向旋转,(如图1)还能得到BE=DG吗?如果能,请给出证明.如若不能,请说明理由:(2)、把背景中的正方形分别改为菱形AEFG和菱形ABCD,将菱形AEFG绕点A按顺时针方向旋转,(如图2)试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG仍成立?请说明理由;(3)、把背景中的正方形改成矩形AEFG和矩形ABCD,且 ,AE=4,AB=8,将矩形AEFG绕点A按顺时针方向旋转(如图3),连接DE,BG.小组发现:在旋转过程中, BG2+DE2是定值,请求出这个定值.35. 如图,点 是反比例函数 ( )图象上一点,过点 分别向坐标轴作垂线,垂足为 , ,反比例函数 ( )的图象经过 的中点 ,与 , 分别相交于点 , .连接 并延长交 轴于点 ,点 与点 关于点 对称,连接 , .
(1)、将正方形AEFG绕点A按逆时针方向旋转,(如图1)还能得到BE=DG吗?如果能,请给出证明.如若不能,请说明理由:(2)、把背景中的正方形分别改为菱形AEFG和菱形ABCD,将菱形AEFG绕点A按顺时针方向旋转,(如图2)试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG仍成立?请说明理由;(3)、把背景中的正方形改成矩形AEFG和矩形ABCD,且 ,AE=4,AB=8,将矩形AEFG绕点A按顺时针方向旋转(如图3),连接DE,BG.小组发现:在旋转过程中, BG2+DE2是定值,请求出这个定值.35. 如图,点 是反比例函数 ( )图象上一点,过点 分别向坐标轴作垂线,垂足为 , ,反比例函数 ( )的图象经过 的中点 ,与 , 分别相交于点 , .连接 并延长交 轴于点 ,点 与点 关于点 对称,连接 , .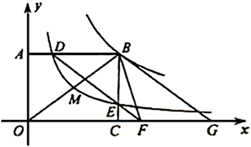 (1)、填空: ;(2)、求 的面积;(3)、求证:四边形 为平行四边形.36. 如图,在菱形ABCD中, , ,点E为边AB上一个动点,延长BA到点F , 使 ,且CF、DE相交于点G
(1)、填空: ;(2)、求 的面积;(3)、求证:四边形 为平行四边形.36. 如图,在菱形ABCD中, , ,点E为边AB上一个动点,延长BA到点F , 使 ,且CF、DE相交于点G (1)、当点E运动到AB中点时,证明:四边形DFEC是平行四边形;(2)、当 时,求AE的长;(3)、当点E从点A开始向右运动到点B时,求点G运动路径的长度.
(1)、当点E运动到AB中点时,证明:四边形DFEC是平行四边形;(2)、当 时,求AE的长;(3)、当点E从点A开始向右运动到点B时,求点G运动路径的长度.