广东省中考数学真题汇编(近三年) 专题7 图形的性质----三角形和多边形
试卷更新日期:2021-08-25 类型:二轮复习
一、单选题
-
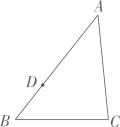
1. 如图,已知AB=AC,BC=6,尺规作图痕迹可求出BD=( )
 A、2 B、3 C、4 D、52. 如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )
A、2 B、3 C、4 D、52. 如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )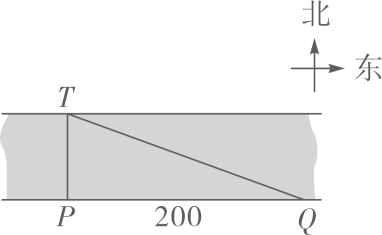 A、200tan70°米 B、 米 C、200sin70°米 D、 米3. 一把直尺与30°的直角三角板如图所示,∠1=40°,则∠2=( )
A、200tan70°米 B、 米 C、200sin70°米 D、 米3. 一把直尺与30°的直角三角板如图所示,∠1=40°,则∠2=( ) A、50° B、60° C、70° D、80°4. 以下说法正确的是( )A、平行四边形的对边相等 B、圆周角等于圆心角的一半 C、分式方程 的解为x=2 D、三角形的一个外角等于两个内角的和5. 如图, 中, , , ,以点 为圆心, 为半径作 ,当 时, 与 的位置关系是( )
A、50° B、60° C、70° D、80°4. 以下说法正确的是( )A、平行四边形的对边相等 B、圆周角等于圆心角的一半 C、分式方程 的解为x=2 D、三角形的一个外角等于两个内角的和5. 如图, 中, , , ,以点 为圆心, 为半径作 ,当 时, 与 的位置关系是( ) A、相离 B、相切 C、相交 D、无法确定6. 若一个多边形的内角和是540°,则该多边形的边数为( )A、4 B、5 C、6 D、77. 中,点 分别是 的边 , 的中点,连接 ,若 ,则 ( )A、 B、 C、 D、8. 已知 的周长为16,点 , , 分别为 三条边的中点,则 的周长为( )A、8 B、 C、16 D、49. 下面命题正确的是( )A、矩形对角线互相垂直 B、方程x2=14x的解为x=14 C、六边形内角和为540° D、一条斜边和一条直角边分别相等的两个直角三角形全等10. 如图,已知l1∥AB,AC为角平分线,下列说法错误的是( )
A、相离 B、相切 C、相交 D、无法确定6. 若一个多边形的内角和是540°,则该多边形的边数为( )A、4 B、5 C、6 D、77. 中,点 分别是 的边 , 的中点,连接 ,若 ,则 ( )A、 B、 C、 D、8. 已知 的周长为16,点 , , 分别为 三条边的中点,则 的周长为( )A、8 B、 C、16 D、49. 下面命题正确的是( )A、矩形对角线互相垂直 B、方程x2=14x的解为x=14 C、六边形内角和为540° D、一条斜边和一条直角边分别相等的两个直角三角形全等10. 如图,已知l1∥AB,AC为角平分线,下列说法错误的是( )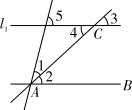 A、∠1=∠4 B、∠1=∠5 C、∠2=∠3 D、∠1=∠311. 如图,已知AB=AC,AB=5,BC=3,以AB两点为圆心,大于 AB的长为半径画圆弧,两弧相交于点M、N,连接MN与AC相交于点D,则△BDC的周长为( )
A、∠1=∠4 B、∠1=∠5 C、∠2=∠3 D、∠1=∠311. 如图,已知AB=AC,AB=5,BC=3,以AB两点为圆心,大于 AB的长为半径画圆弧,两弧相交于点M、N,连接MN与AC相交于点D,则△BDC的周长为( )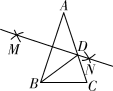 A、8 B、10 C、11 D、1312. 设O为坐标原点,点A、B为抛物线 上的两个动点,且 .连接点A、B , 过O作 于点C , 则点C到y轴距离的最大值( )A、 B、 C、 D、1
A、8 B、10 C、11 D、1312. 设O为坐标原点,点A、B为抛物线 上的两个动点,且 .连接点A、B , 过O作 于点C , 则点C到y轴距离的最大值( )A、 B、 C、 D、1二、填空题
-
13. 如图,在 中, , ,线段AB的垂直平分线分别交AC、AB于点D、E , 连结BD . 若 ,则AD的长为 .
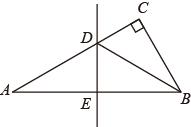 14. 如图,在 中, , ,点D是边AB上一点,点B关于直线CD的对称点为 ,当 时,则 的度数为 .
14. 如图,在 中, , ,点D是边AB上一点,点B关于直线CD的对称点为 ,当 时,则 的度数为 . 15. 如图,在 中,D , E分别为 , 上的点,将 沿 折叠,得到 ,连接 , , ,若 , , ,则 的长为.
15. 如图,在 中,D , E分别为 , 上的点,将 沿 折叠,得到 ,连接 , , ,若 , , ,则 的长为.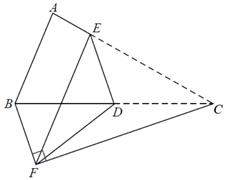 16. 如图,已知 , 是角平分线且 ,作 的垂直平分线交 于点F , 作 ,则 周长为 .
16. 如图,已知 , 是角平分线且 ,作 的垂直平分线交 于点F , 作 ,则 周长为 .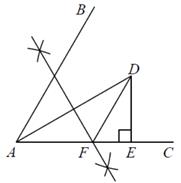 17. 如图,点A,B,C在直线l上,PB⊥l , PA=6cm,PB=5cm,PC=7cm,则点P到直线l的距离是cm.
17. 如图,点A,B,C在直线l上,PB⊥l , PA=6cm,PB=5cm,PC=7cm,则点P到直线l的距离是cm.
 18. 有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图, ,点 , 分别在射线 , 上, 长度始终保持不变, , 为 的中点,点 到 , 的距离分别为4和2.在此滑动过程中,猫与老鼠的距离 的最小值为 .
18. 有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图, ,点 , 分别在射线 , 上, 长度始终保持不变, , 为 的中点,点 到 , 的距离分别为4和2.在此滑动过程中,猫与老鼠的距离 的最小值为 .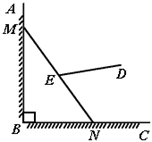
三、解答题
-
19. 如图,点E、F在线段BC上, , , ,证明: .
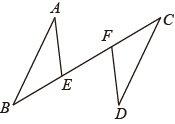 20. 如图, , , .求 的度数.
20. 如图, , , .求 的度数.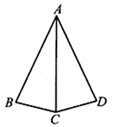 21. 如图,在 中,点 , 分别是 、 边上的点, , , 与 相交于点 ,求证: 是等腰三角形.
21. 如图,在 中,点 , 分别是 、 边上的点, , , 与 相交于点 ,求证: 是等腰三角形.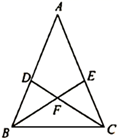 22. 如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,求证:
22. 如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,求证: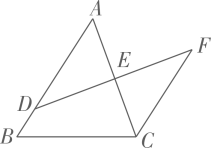
四、作图题
-
23. 如图, 中, .(1)、作点 关于 的对称点 ;(要求:尺规作图,不写作法,保留作图痕迹)
 (2)、在(1)所作的图中,连接 , ,连接 ,交 于点 .
(2)、在(1)所作的图中,连接 , ,连接 ,交 于点 .①求证:四边形 是菱形;
②取 的中点 ,连接 ,若 , ,求点 到 的距离.
五、综合题
-
24. 如图,在四边形ABCD中, ,点E是AC的中点,且
 (1)、尺规作图:作 的平分线AF , 交CD于点F , 连结EF、BF(保留作图痕迹,不写作法);(2)、在(1)所作的图中,若 ,且 ,证明: 为等边三角形.25. 如图,在 中, ,作 的垂直平分线交 于点D , 延长 至点E , 使 .
(1)、尺规作图:作 的平分线AF , 交CD于点F , 连结EF、BF(保留作图痕迹,不写作法);(2)、在(1)所作的图中,若 ,且 ,证明: 为等边三角形.25. 如图,在 中, ,作 的垂直平分线交 于点D , 延长 至点E , 使 . (1)、若 ,求 的周长;(2)、若 ,求 的值.
(1)、若 ,求 的周长;(2)、若 ,求 的值.
-