广东省中考数学真题汇编(近三年) 专题5 图形的性质----圆
试卷更新日期:2021-08-25 类型:二轮复习
一、单选题
-
1. 一根钢管放在V形架内,其横截面如图所示,钢管的半径是24cm,若 ,则劣弧AB的长是( )
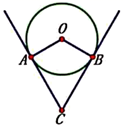 A、 B、 C、 D、2. 如图, 是⊙O的直径,点C为圆上一点, 的平分线交 于点D , ,则⊙O的直径为( )
A、 B、 C、 D、2. 如图, 是⊙O的直径,点C为圆上一点, 的平分线交 于点D , ,则⊙O的直径为( ) A、 B、 C、1 D、23. 往直径为 的圆柱形容器内装入一些水以后,截面如图所示,若水面宽 ,则水的最大深度为( )
A、 B、 C、1 D、23. 往直径为 的圆柱形容器内装入一些水以后,截面如图所示,若水面宽 ,则水的最大深度为( )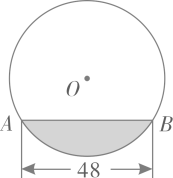 A、 B、 C、 D、4. 如图, 中, , , ,以点 为圆心, 为半径作 ,当 时, 与 的位置关系是( )
A、 B、 C、 D、4. 如图, 中, , , ,以点 为圆心, 为半径作 ,当 时, 与 的位置关系是( ) A、相离 B、相切 C、相交 D、无法确定5. 平面内,⊙O的半径为1,点P到O的距离为2,过点P可作⊙O的切线条数为( )A、0条 B、1条 C、2条 D、无数条6. 设O为坐标原点,点A、B为抛物线 上的两个动点,且 .连接点A、B , 过O作 于点C , 则点C到y轴距离的最大值( )A、 B、 C、 D、1
A、相离 B、相切 C、相交 D、无法确定5. 平面内,⊙O的半径为1,点P到O的距离为2,过点P可作⊙O的切线条数为( )A、0条 B、1条 C、2条 D、无数条6. 设O为坐标原点,点A、B为抛物线 上的两个动点,且 .连接点A、B , 过O作 于点C , 则点C到y轴距离的最大值( )A、 B、 C、 D、1二、填空题
-
7. 如图,等腰直角三角形 中, .分别以点B、点C为圆心,线段 长的一半为半径作圆弧,交 、 、 于点D、E、F , 则图中阴影部分的面积为 .
 8. 在 中, .点D为平面上一个动点, ,则线段 长度的最小值为 .9. 如图,正方形ABCD的边长为4,点E是边BC上一点,且 ,以点A为圆心,3为半径的圆分别交AB、AD于点F、G , DF与AE交于点H . 并与 交于点K , 连结HG、CH . 给出下列四个结论.(1)H是FK的中点;(2) ;(3) ;(4) ,其中正确的结论有(填写所有符合题意结论的序号).
8. 在 中, .点D为平面上一个动点, ,则线段 长度的最小值为 .9. 如图,正方形ABCD的边长为4,点E是边BC上一点,且 ,以点A为圆心,3为半径的圆分别交AB、AD于点F、G , DF与AE交于点H . 并与 交于点K , 连结HG、CH . 给出下列四个结论.(1)H是FK的中点;(2) ;(3) ;(4) ,其中正确的结论有(填写所有符合题意结论的序号).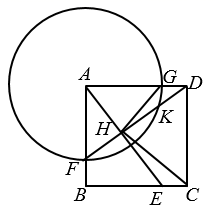
三、综合题
-
10. 如图,在四边形 中, ,点E、F分别在线段 、 上,且 .
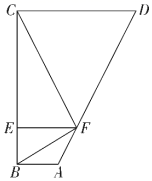 (1)、求证: ;(2)、求证:以 为直径的圆与 相切;(3)、若 ,求 的面积.11. 如图, 为 的弦,D , C为 的三等分点, .
(1)、求证: ;(2)、求证:以 为直径的圆与 相切;(3)、若 ,求 的面积.11. 如图, 为 的弦,D , C为 的三等分点, .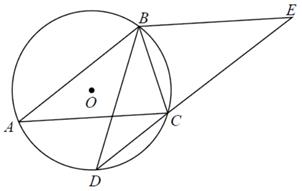 (1)、求证: ;(2)、若 , ,求 的长.12. 如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E.
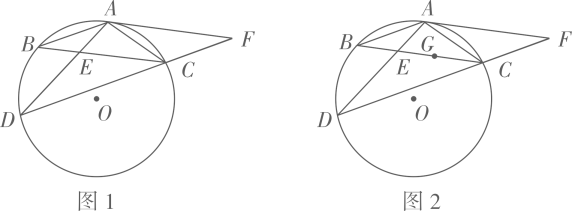
(1)、求证: ;(2)、若 , ,求 的长.12. 如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E. (1)、求证:AE=AB;(2)、若AB=10,BC=6,求CD的长.13. 如图1,在四边形 中, , , 是 的直径, 平分 .
(1)、求证:AE=AB;(2)、若AB=10,BC=6,求CD的长.13. 如图1,在四边形 中, , , 是 的直径, 平分 .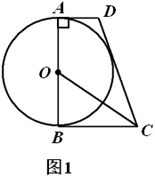 (1)、求证:直线 与 相切;(2)、如图2,记(1)中的切点为 , 为优弧 上一点, , .求 的值.
(1)、求证:直线 与 相切;(2)、如图2,记(1)中的切点为 , 为优弧 上一点, , .求 的值.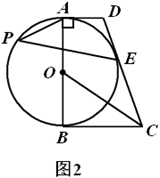 14. 已知在平面直角坐标系中,点A(3,0),B(-3,0),C(-3,8),以线段BC为直径作圆,圆心为E,直线AC交□E于点D,连接OD.
14. 已知在平面直角坐标系中,点A(3,0),B(-3,0),C(-3,8),以线段BC为直径作圆,圆心为E,直线AC交□E于点D,连接OD.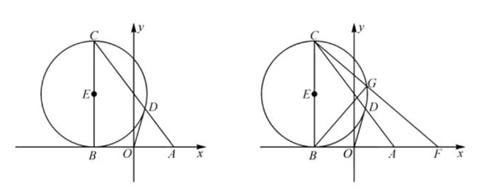 (1)、求证:直线OD是□E的切线;(2)、点F为x轴上任意一点,连接CF交□E于点G,连接BG:
(1)、求证:直线OD是□E的切线;(2)、点F为x轴上任意一点,连接CF交□E于点G,连接BG:当tan∠FCA= ,求所有F点的坐标(直接写出);
15. 在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫格点, 的三个顶点均在格点上,以点 为圆心的 与 相切于点 ,分别交 、 于点 、 .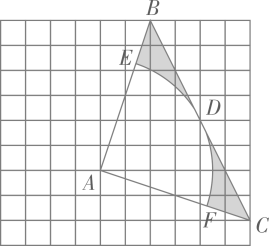 (1)、求 三边的长;(2)、求图中由线段 、 、 及 所围成的阴影部分的面积.16. 如图,⊙O的直径AB=10,弦AC=8,连接BC。
(1)、求 三边的长;(2)、求图中由线段 、 、 及 所围成的阴影部分的面积.16. 如图,⊙O的直径AB=10,弦AC=8,连接BC。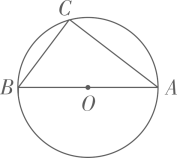 (1)、尺规作图:作弦CD,使CD=BC(点D不与B重合),连接AD;(保留作图痕迹,不写作法)(2)、在(1)所作的图中,求四边形ABCD的周长。17. 如图, 为等边 的外接圆,半径为2,点 在劣弧 上运动(不与点 重合),连接 , , .
(1)、尺规作图:作弦CD,使CD=BC(点D不与B重合),连接AD;(保留作图痕迹,不写作法)(2)、在(1)所作的图中,求四边形ABCD的周长。17. 如图, 为等边 的外接圆,半径为2,点 在劣弧 上运动(不与点 重合),连接 , , .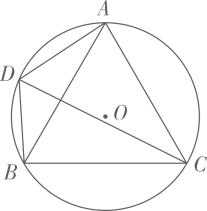 (1)、求证: 是 的平分线;(2)、四边形 的面积 是线段 的长 的函数吗?如果是,求出函数解析式;如果不是,请说明理由;(3)、若点 分别在线段 , 上运动(不含端点),经过探究发现,点 运动到每一个确定的位置, 的周长有最小值 ,随着点 的运动, 的值会发生变化,求所有 值中的最大值.
(1)、求证: 是 的平分线;(2)、四边形 的面积 是线段 的长 的函数吗?如果是,求出函数解析式;如果不是,请说明理由;(3)、若点 分别在线段 , 上运动(不含端点),经过探究发现,点 运动到每一个确定的位置, 的周长有最小值 ,随着点 的运动, 的值会发生变化,求所有 值中的最大值.