2022年苏科版初中数学《中考一轮复习》专题一 数与式 1.5 二次根式
试卷更新日期:2021-08-25 类型:一轮复习
一、单选题
-
1. 在式子 , , , , , 中,是二次根式的有( )A、3个 B、4个 C、5个 D、6个2. 下列各式中,为最简二次根式的是( )A、 B、 C、 D、3. 使 成立的x的取值范围是( )A、 B、 C、 且 D、4. 下列计算正确的是( )A、 3 B、 C、 D、( )2=25. 下列式子与 可以进行合并的是( )A、 B、 C、 D、6. 是某三角形三边的长,则 等于( )A、 B、 C、10 D、47. 已知 , ,则 的值为( )A、14 B、12 C、16 D、8. 二次根式 , , 的大小关系是( )A、 < < B、 < < C、 < < D、 < <9. 若 ,则 的值为: ( )
A、0 B、1 C、-1 D、210. 已知 , , 表示取三个数中最大的那个数﹒例如:当 , , , = , , =81﹒当 , , = 时,则 的值为( )A、 B、 C、 D、二、填空题
-
11. 若二次根式 在实数范围内有意义,则 的取值范围是.12. 已知 与最简二次根式 是同类二次根式,则a的值是.13. 比较大小: .14. 若 ,则 的取值范围是 .15. 计算( +1)2015( ﹣1)2014=
16. 已知, ,当x分别取1,2,3,…,2021时,所对应的y值的总和是.17. 若实数a,b,c满足关系式 ,则c= .18. 如果(x﹣ )(y﹣ )=2008,求3x2﹣2y2+3x﹣3y﹣2007= .三、计算题
-
19. 计算:(1)、(2)、20.(1)、计算:(2)、
四、解答题
-
21. 已知a+b=-6,ab=5,求b +a 的值.22. 如图,a,b,c是数轴上三个点A、B、C所对应的实数.试化简: .
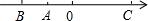 23. 已知 .(1)、求 , 的值;(2)、求 的算术平方根.24. 阅读理解:
23. 已知 .(1)、求 , 的值;(2)、求 的算术平方根.24. 阅读理解:∵ ,即2< <3,∴1< -1<2,
∴ -1的整数部分为1,
∴ -1的小数部分为 -2
解决问题:
已知a是 -3的整数部分,b是 -3的小数部分,求(-a)3+(b+4)2的平方根
25. 阅读下面的问题:;
……
(1)、求 与 的值.(2)、已知n是正整数,求 与 的值;(3)、计算 .26. 阅读下列解题过程例:若代数式 的值是2,求a的取值范围.
解:原式=|a﹣1|+|a﹣3|,
当a<1时,原式=(1﹣a)+(3﹣a)=4﹣2a=2,解得a=1(舍去);
当1≤a≤3时,原式=(a﹣1)+(3﹣a)=2=2,符合条件;
当a>3时,原式=(a﹣1)+(a﹣3)=2a﹣4=2,解得a=3(舍去)
所以,a的取值范围是1≤a≤3
上述解题过程主要运用了分类讨论的方法,请你根据上述理解,解答下列问题
(1)、当2≤a≤5时,化简: = 3 ;(2)、若等式 =4成立,则a的取值范围是 3≤a≤7 ;(3)、若 =8,求a的取值.27. 阅读下述材料:我们在学习二次根式时,熟悉的分母有理化以及应用.其实,有一个类似的方法叫做“分子有理化”:
与分母有理化类似,分母和分子都乘以分子的有理化因式,从而消掉分子中的根式.比如:
分子有理化可以用来比较某些二次根式的大小,也可以用来处理一些二次根式的最值问题.例如:比较 和 的大小.可以先将它们分子有理化.如下:
因为 ,所以
再例如:求 的最大值.做法如下:
解:由 , 可知 ,而
当 时,分母 有最小值 ,所以y的最大值是 .
解决下述问题:
(1)、比较 和 的大小;(2)、求 的最大值.28. 由 得, ;如果两个正数a,b,即 ,则有下面的不等式: ,当且仅当 时取到等号.例如:已知 ,求式子 的最小值.
解:令 ,则由 ,得 ,当且仅当 时,即 时,式子有最小值,最小值为4.

请根据上面材料回答下列问题:
(1)、当 ,式子 的最小值为;当 ,则当 时,式子 取到最大值;(2)、用篱笆围一个面积为32平方米的长方形花园,使这个长方形花园的一边靠墙(墙长20米),问这个长方形的长、宽各为多少时,所用的篱笆最短,最短的篱笆是多少?(3)、如图,四边形 的对角线 、 相交于点O, 、 的面积分别是8和14,求四边形 面积的最小值.