2022年苏科版初中数学《中考一轮复习》专题一数与式 1.4 分式

试卷更新日期：2021-08-25 类型：一轮复习

进入出卷网下载

一、单选题

1. 在 $\frac{1}{x}$ 、 $\frac{1}{2}$ 、 $\frac{3 x y}{π}$ 、 $\frac{x^{2} - 2 y^{3}}{x + 3 y}$ 、 $\frac{x^{2} + 1}{5}$ 、 $\frac{m - n}{7 a b}$ 中，分式的个数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 函数 $y = \frac{\sqrt{x + 2}}{x - 3}$ 的自变量 $x$ 的取值范围是（）

A、 $x \geq - 2$ 且 $x \neq 3$ B、 $x > - 2$ 且 $x \neq 3$ C、 $x \neq - 2$ 且 $x \neq 3$ D、 $x \neq - 2$ 且 $x > 3$

查看试题解析
3. 若分式 $\frac{| x | - 5}{x + 5}$ 的值为0，则 $x$ 的值为（）

A、-5 B、5 C、-5和5 D、无法确定

查看试题解析
4. 下列各式正确的是（）

A、 $\frac{c}{- a - b} = - \frac{c}{a - b}$ B、 $\frac{c}{- a - b} = - \frac{c}{a + b}$
C、 $\frac{c}{- a + b} = - \frac{c}{a + b}$ D、 $\frac{c}{- a - b} = - \frac{- c}{a - b}$

查看试题解析
5. 对分式 $\frac{1}{a - b}, \frac{1}{a + b}, \frac{1}{a^{2} - b^{2}}$ 通分后， $\frac{1}{a + b}$ 的结果是（）

A、 $\frac{a + b}{a^{2} - b^{2}}$ B、 $\frac{a - b}{a^{2} - b^{2}}$ C、 $\frac{a^{2} - b^{2}}{(a + b) (a^{2} - b^{2})}$ D、 $\frac{(a + b) (a - b)}{{(a^{2} - b^{2})}^{2}}$

查看试题解析
6. 如果把分式 $\frac{3 x + y}{x - y}$ 中的 $x$ 和 $y$ 都扩大为原来的2倍，那么分式的值（）

A、缩小到原来的 $\frac{1}{2}$ B、不变 C、扩大到原来的2倍 D、扩大到原来的4倍

查看试题解析
7. 已知 $\frac{1}{m} - \frac{1}{n} = 6$ ，则 $\frac{m n}{m - n}$ 的值为（）

A、6 B、-6 C、 $\frac{1}{6}$ D、 $- \frac{1}{6}$

查看试题解析
8. 计算 $\frac{a^{2} - 4}{a} \div (a + 1 - \frac{5 a - 4}{a})$ 的结果是（）

A、 $\frac{a + 2}{a - 2}$ B、 $\frac{a - 2}{a + 2}$ C、 $\frac{{(a - 2)}^{2} (a + 2)}{a}$ D、 $\frac{a + 2}{a}$

查看试题解析
9. 已知代数式 $\frac{6}{2 x - 1}$ 的值是一个整数，则整数x有（　　　）

A、2个 B、3个 C、4个 D、无数个

查看试题解析
10. 已知实数x、y、z满足 $\frac{x}{y + z} + \frac{y}{z + x} + \frac{z}{x + y} = 1$ ，则 $\frac{x^{2}}{y + z} + \frac{y^{2}}{z + x} + \frac{z^{2}}{x + y}$ 的值（）

A、-1 B、0 C、1 D、2

查看试题解析

二、填空题

11. 数据0.000000407用科学记数法表示为.

查看试题解析
12. 若（t-3）^t-2=1，则t=.

查看试题解析
13. 一组按规律排列的式子： $- \frac{b^{2}}{a}$ ， $\frac{b^{5}}{a^{2}}$ ， $- \frac{b^{8}}{a^{3}}$ ， $\frac{b^{11}}{a^{4}}$ ，…（ab≠0），其中第7个式子是，第n个式子是（n为正整数）．

查看试题解析
14. 当整数x＝时，分式 $\frac{2 x + 2}{x^{2} - 1}$ 的值为正整数．

查看试题解析
15. 当 $x = \sqrt{2021} + 3$ 时，代数式 $(\frac{x + 3}{x^{2} - 3 x} - \frac{x - 1}{x^{2} - 6 x + 9}) \div \frac{x - 9}{x}$ 的值是．

查看试题解析
16. 已知 $a^{2} - a b + b^{2} = 0 (a \neq 0 ， b \neq 0)$ ，则式子 $\frac{b}{a} + \frac{a}{b}$ 的值等于

查看试题解析
17. x ， y为实数，且满足 $y = \frac{2 x + 2}{x^{2} + 3 x + 3}$ ，则y的最大值是．

查看试题解析
18. 若|a﹣1|+（ab﹣2）²＝0，则 $\frac{1}{a b} + \frac{1}{(a + 1) (b + 1)}$ $+$ … $+$ $\frac{1}{(a + 10) (b + 10)}$ ＝.

查看试题解析

三、解答题

19. 化简：

(1)、 $\frac{2 a x^{2} y}{3 a x y^{2}}$ ；

(2)、 $\frac{x^{2}}{x - 5} + \frac{25}{5 - x}$ ；

(3)、 $(1 - \frac{1}{1 - x}) + \frac{x}{x - 1}$ ；

(4)、 $(\frac{a^{2}}{a + 1} - a + 1) + \frac{a^{2} - 1}{a^{2} + 2 a + 1}$ .

查看试题解析
20. 若 $\frac{x}{3} = \frac{y}{4} = \frac{z}{5}$ ，且 $3 x - 2 y + z = 18$ ，求 $x + 5 y - 3 z$ 的值.

查看试题解析
21. 先化简，再求值： $(a - \frac{a^{2}}{a + 1}) \div \frac{a^{2}}{a^{2} - 1}$ ，其中 $a = 2 \tan 45 ° + 1$ ．

查看试题解析
22. 先化简，再求值 $\frac{x^{2} + 6 x + 9}{x + 2} \div (\frac{5}{x + 2} + 2 - x)$ ，其中x是方程 $x^{2} + x - 2 = 0$ 的解.

查看试题解析
23. 先化简 $(\frac{a^{2} - 2 a + 1}{a^{2} - a} + \frac{a^{2} - 4}{a^{2} + 2 a}) \div \frac{2 a - 3}{a + 1}$ ；然后再从 $- 3$ ， $- 2$ ， $- 1$ ，0，1选择一个合适的数作为a的值，代入后再求值．

查看试题解析
24. 先化简，再求值： $\frac{x^{2} - 4 x + 4}{x + 1} \div (\frac{3}{x + 1} - x + 1)$ ，请从不等式组 ${\begin{matrix} 7 - 3 x \geq 1 \\ 2 x + 7 \geq 3 \end{matrix}$ 的整数解中选择一个合适的值代入求值．

查看试题解析
25. 已知 $\frac{A}{x - 1} - \frac{B}{2 - x} = \frac{2 x - 6}{(x - 1) (x - 2)}$ ，求A、B的值.

查看试题解析
26. 上课时老师在黑板上书写了一个分式的正确化简结果，随后用手掌盖住了一部分，形式如下：

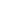(1)、聪明的你请求出盖住部分化简后的结果

(2)、当 $x = 2$ 时， $y$ 等于何值时，原分式的值为5

查看试题解析
27. 观察下列各式：
① $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ；

② $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ；

③ $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ；

④ $\frac{1}{4 \times 5} = \frac{1}{4} - \frac{1}{5}$ …

(1)、请用以上规律计算： $\frac{1}{2} + \frac{1}{6} + \frac{1}{12} + \frac{1}{20} + \dots + \frac{1}{90} =$ ；

(2)、若 $\frac{1}{(m + 1) (m + 2)} + \frac{1}{(m + 2) (m + 3)} + \frac{1}{(m + 3) (m + 4)} + \dots$
$+ \frac{1}{(m + 2020) (m + 2021)}$ $= \frac{1}{m + 2021}$ ，求 $m$ 的值．

查看试题解析
28. （阅读材料）
小慧同学数学写作片段

乘法公式“大家族”

学习《整式的乘法及因式分解》之后，我发现乘法公式不只是教材上“黑体字”明确的“平方差公式 $(a + b) (a - b) = a^{2} - b^{2}$ ”“完全平方公式 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ 和 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ ”，其实在教材或平时的练习中还“隐含”一些“乘法公式”值得积累，比如，

$(a + b) (a^{2} - a b + b^{2}) = a^{3} + b^{3}$ ；

$(a - b) (a^{2} + a b + b^{2}) = a^{3} - b^{3}$ ；

$(x + m) (x + n) = x^{2} + (m + n) x + m n$ ；

${(a + b + c)}^{2} = a^{2} + b^{2} + c^{2} + 2 a b + 2 a c + 2 b c$ .

……

（解题运用）

(1)、在实数范围内因式分解： $x^{2} - (\sqrt{2} + \sqrt{3}) x + \sqrt{6} =$ ；

(2)、设 $x ， y$ 满足等式 $x^{2} + 2 x y + y^{2} - 12 x - 12 y + 36 = 0$ ，求 $2 x + 2 y$ 的值；

(3)、若正数 $a ， b$ 满足等式 $\frac{1}{a} - \frac{1}{b} = \frac{1}{a + b}$ ，求代数式 ${(\frac{b}{a})}^{3} + {(\frac{a}{b})}^{3}$ 的值.

查看试题解析

2022年苏科版初中数学《中考一轮复习》专题一 数与式 1.4 分式

一、单选题

二、填空题

三、解答题

2022年苏科版初中数学《中考一轮复习》专题一数与式 1.4 分式