河南省中考数学真题模拟题分类卷6 统计与概率(近几年)
试卷更新日期:2021-08-25 类型:二轮复习
一、单选题
-
1. 要调查下列问题,适合采用全面调查(普查)的是( )A、中央电视台《开学第--课》 的收视率 B、某城市居民6月份人均网上购物的次数 C、即将发射的气象卫星的零部件质量 D、某品牌新能源汽车的最大续航里程2. 下列说法正确的是( )A、了解河南省初中生身高情况适宜全面调查 B、甲,乙两名射击运动员5次射击成绩的方差分别为s甲2=1.2,s乙2=2,说明甲的射击成绩比乙的射击成绩稳定 C、同旁内角互补是必然事件 D、已知某篮球运动员投篮投中的概率为0.6,则他投10次一定可投中6次3. 某学校对学生的期末操行评语成绩按班委评分、任课教师评分、家长评分三方面确定成绩(评分满分均为100分),若三方面依次按2:5:3确定成绩,且某同学所评的得分依次为90分、92分、91分,则该同学评分的最后得分是( )A、91分 B、91.3分 C、91.2分 D、91.1分4. 现有4张卡片,正面图案如图所示,它们除此之外完全相同.把这4张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面图案恰好是“天问”和“九章”的概率是( )
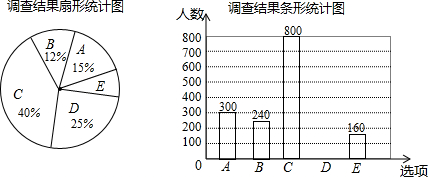
 A、 B、 C、 D、5. 某超市销售A,B,C,D四种矿泉水,它们的单价依次是5元、3元、2元、1元.某天的销售情况如图所示,则这天销售的矿泉水的平均单价是( )
A、 B、 C、 D、5. 某超市销售A,B,C,D四种矿泉水,它们的单价依次是5元、3元、2元、1元.某天的销售情况如图所示,则这天销售的矿泉水的平均单价是( )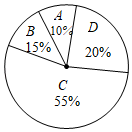 A、1.95元 B、2.15元 C、2.25元 D、2.75元6. 河南省旅游资源丰富,2013~2017年旅游收入不断增长,同比增速分别为:15.3%,12.7%,15.3%,14.5%,17.1%.关于这组数据,下列说法正确的是( )
A、1.95元 B、2.15元 C、2.25元 D、2.75元6. 河南省旅游资源丰富,2013~2017年旅游收入不断增长,同比增速分别为:15.3%,12.7%,15.3%,14.5%,17.1%.关于这组数据,下列说法正确的是( )
A、中位数是12.7% B、众数是15.3% C、平均数是15.98% D、方差是07. 现有4张卡片,其中3张卡片正面上的图案是“ ”,1张卡片正面上的图案是“
”,1张卡片正面上的图案是“  ”,它们除此之外完全相同.把这4张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面图案相同的概率是( )
”,它们除此之外完全相同.把这4张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面图案相同的概率是( )
A、 B、 C、 D、8. 我们从电视上看到一些大型比赛,通常有若干个评委现场打分,在公布得分时,主持人会说:“去掉一个最高分,去掉一个最低分, 的最后得分是…’根据你的经验,去掉一个最高分和一个最低分之后,统计量一定不会发生变化的是( )A、平均数 B、众数 C、方差 D、中位数9. 某校开展“疫情防控小卫士”活动,从学生会“督查部”的4名学生(2男2女)中随机选两名进行督导每日一次体温测量,恰好选中男女学生各一名的概率是( )A、 B、 C、 D、二、填空题
-
10. 在一个不透明的袋子里,放着标有数字2、5、7、8的四个小球(除数字不同外,其余都相同),在看不见的情况下随机摸出2个球,则摸出的两个球上的数字的和不小于10的概率是.11. 一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是.
 12. 某外贸公司要出口一批规格为 克/盒的红枣,现有甲、乙两个厂家提供货源,它们的价格相同,品质也相近.质检员从两厂的产品中各随机抽取 盒进行检测,测得它们的平均质量均为 克,每盒红枣的质量如图所示,则产品更符合规格要求的厂家是.(填“甲”或“乙”)
12. 某外贸公司要出口一批规格为 克/盒的红枣,现有甲、乙两个厂家提供货源,它们的价格相同,品质也相近.质检员从两厂的产品中各随机抽取 盒进行检测,测得它们的平均质量均为 克,每盒红枣的质量如图所示,则产品更符合规格要求的厂家是.(填“甲”或“乙”)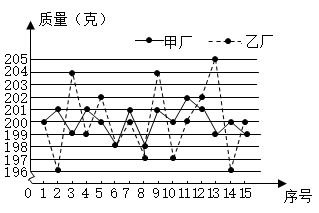 13. 如图所示的转盘,被分成面积相等的四个扇形,分别涂有红、黄、蓝、绿四种颜色.固定指针,自由转动转盘两次,每次停止后,记下指针所指区域(指针指向区域分界线时,忽略不计)的颜色,则两次颜色相同的概率是.
13. 如图所示的转盘,被分成面积相等的四个扇形,分别涂有红、黄、蓝、绿四种颜色.固定指针,自由转动转盘两次,每次停止后,记下指针所指区域(指针指向区域分界线时,忽略不计)的颜色,则两次颜色相同的概率是. 14. 现有两个不透明的袋子,一个装有2个红球、1个白球,另一个装有1个黄球、2个红球,这些球除颜色外完全相同.从两个袋子中各随机摸出1个球,摸出的两个球颜色相同的概率是.15. 几何图形嵌板是一种开发幼儿智力的玩具.如图,甲,乙两个小朋友分别从 , , , 四个嵌板中随机抓取一个,放在操作屉中,则他们抓取相同嵌板的概率为 .
14. 现有两个不透明的袋子,一个装有2个红球、1个白球,另一个装有1个黄球、2个红球,这些球除颜色外完全相同.从两个袋子中各随机摸出1个球,摸出的两个球颜色相同的概率是.15. 几何图形嵌板是一种开发幼儿智力的玩具.如图,甲,乙两个小朋友分别从 , , , 四个嵌板中随机抓取一个,放在操作屉中,则他们抓取相同嵌板的概率为 . 16. 某社团中有三名男生和一名女生,该社团将随机选派两名同学作为代表参加市级比赛,恰好选中一男一女的概率是.
16. 某社团中有三名男生和一名女生,该社团将随机选派两名同学作为代表参加市级比赛,恰好选中一男一女的概率是.三、综合题
-
17. 2021年4月,教育部印发《关于进一步加强中小学生睡眠管理工作的通知》,明确要求初中生每天睡眠时间应达到9小时.某初级中学为了解学生睡眠时间的情况,从本校学生中随机抽取500名进行卷调查,并将调查结果用统计图描述如下.
调查问卷
1近两周你平均每天睡眠时间大约是 小时.
如果你平均每天睡眠时间不足9小时,请回答第2个问题
2影响你睡眠时间的主要原因是 .(单选)
A.校内课业负担重 B.校外学习任务重 C.学习效率低 D.其他

平均每天睡眠时间 (时)分为 组:① ;② ;③ ;④ ;⑤ .
根据以上信息,解答下列问题:
(1)、本次调查中,平均每天睡眠时间的中位数落在第(填序号)组,达到 小时的学生人数占被调查人数的百分比为;(2)、请对该校学生睡眠时间的情况作出评价,并提出两条合理化建议.18. 为发展乡村经济,某村根据本地特色,创办了山药粉加工厂.该厂需购置一台分装机,计划从商家推荐试用的甲、乙两台不同品牌的分装机中选择.试用时,设定分装的标准质量为每袋 ,与之相差大于 为不合格.为检验分装效果,工厂对这两台机器分装的成品进行了抽样和分析,过程如下:[收集数据]从甲、乙两台机器分装的成品中各随机抽取 袋,测得实际质量(单位: )
如下:
甲:
乙:
[整理数据]整理以上数据,得到每袋质量 的频数分布表.
485≤x<490 490≤x<495 495≤x<500 500≤x<505 505≤x<510 510≤x<515 甲 2 2 4 7 4 1 乙 1 3 5 7 3 1 [分析数据]根据以上数据,得到以下统计量.

平均数 中位数 方差 不合格率 甲 499.7 501.5 42.01 b 乙 499.7 a 31.81 10% 根据以上信息,回答下列问题:
(1)、表格中的(2)、综合上表中的统计量,判断工厂应选购哪一台分装机,并说明理由.19. 某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:a.七年级成绩频数分布直方图:
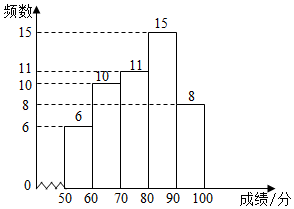
b.七年级成绩在 这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级
平均数
中位数
七
76.9
m
八
79.2
79.5
根据以上信息,回答下列问题:
(1)、在这次测试中,七年级在80分以上(含80分)的有人;(2)、表中m的值为;(3)、在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;(4)、该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.20. 每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如下尚不完整的统计图.治理杨絮一一您选哪一项?(单选)
A.减少杨树新增面积,控制杨树每年的栽种量
B.调整树种结构,逐渐更换现有杨树
C.选育无絮杨品种,并推广种植
D.对雌性杨树注射生物干扰素,避免产生飞絮
E.其他
根据以上统计图,解答下列问题:
(1)、本次接受调查的市民共有人;(2)、扇形统计图中,扇形E的圆心角度数是;
(3)、请补全条形统计图;(4)、若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
21. 4月23日是“世界读书日”,某校团委发起了“让阅读成为习惯”的读书活动,鼓励学生利用周末积极阅读课外书籍.为了解该校学生周末两天的读书时间,校团委随机调查了八年级部分学生的读书时间 (单位:分钟),把读书时间分为四组: .部分数据信息如下:组和C组的所有数据:
根据调查结来绘制了如下尚不完整的统计图:


请根据以上信息,回答下列问题:
(1)、被调查的学生共有 ▲ 人,并补全频数分布直方图;(2)、在扇形统计图中,C组所对应的扇形圆心角是 ;(3)、若该校八年级共有400名学生,请估计八年级学生中周末两天读书时间不少于90分钟的人数.22. 为了解某校八年级学生一门课程的学习情况,小佳和小丽分别对八年级1班和2班本门课程的期末成绩进行了调查分析.小佳对八年级1班全班学生(25名)的成绩进行分析,过程如下收集、整理数据:表一:
分数段
班级
八年级1班
7
5
10
3
表二:
统计量
班级
平均数
中位数
众数
极差
方差
八年级1班
78
85
36
105.28
小丽用同样的方式对八年级2班全班学生(25名)的成绩进行分析,变数据如下:
统计量
班级
平均数
中位数
众数
极差
方差
八年级2班
75
76
73
44
146.8
根据以上信息,解决下列问题:
(1)、已知八年级1班学生的成绩处在 这一组的数据如下: .根据上述数据,将表二补充完整:(2)、你认为哪个班级的成绩更为优异?请说明理由23. 某校为了解七、八年级学生对“文明知识礼仪”的掌握情况,从七、八年级各随机抽取了25名学生进行相关测试,并对成绩进行整理、描述和分析,部分信息如下:
c.八年级D组测试成绩数据为:90,90,91,92,93,94,94;
d.七、八年级被抽取学生测试成绩的平均数、中位数如下表所示:
平均数
中位数
七年级
87.36
87
八年级
91.36
a
根据所给信息,解答下列问题:
(1)、根据统计图,对比两个年级成绩在90分以上(含90分)的百分比,七年级比八年级;(填“大”或“小”)(2)、表中a的值为;(3)、小华的测试成绩为89分,他的成绩在本年级参加测试的学生中处于中上游,请判断小华是 ▲ 年级的学生,并说明理由;(4)、学校决定对本次测试成绩优异的学生进行奖励,老师从七、八年级各抽取了4名同学的成绩记录如下表:七年级
八年级
学生代码
A
B
C
D
E
F
G
H
成绩
98
93
90
95
87
96

其中有两名同学的成绩被墨汁污染了,但老师说七年级和八年级被抽取的这4名同学中各有2名同学可以获得奖励,于是小明说G和H两名同学中只有一名同学可以获得奖励.请问小明的说法是否正确?并说明理由.
24. 为了了解中学生对父母的关心程度,某校九年级兴趣小组利用课外活动时间随机调查了某市若干名学生对父母关心程度的情况( .给父母送自制的生日礼物; .陪父母聊天; .主动帮父母做家务; .知道母亲或父亲某个人的生日; .知道母亲和父亲的生日),并将调查结果绘制成条形统计图(如图1)和扇形统计图(如图2)(不完整).请你根据图中提供的信息,解答下列问题: (1)、此次调查的学生有人.(2)、将图1补充完整.(3)、在扇形统计图中, 部分所对应的圆心角的度数是.(4)、根据抽样调查结果,请你估计该市90000名中学生中主动帮父母做家务的有多少人?25. 距离中考体考时间越来越近,学校想了解初三年级1512名学生周末在家体育锻炼的情况,在初三年级随机抽取了18名男生和18名女生,对他们周末在家的锻炼时间进行了调查,并收集得到了以下数据(单位:分钟)
(1)、此次调查的学生有人.(2)、将图1补充完整.(3)、在扇形统计图中, 部分所对应的圆心角的度数是.(4)、根据抽样调查结果,请你估计该市90000名中学生中主动帮父母做家务的有多少人?25. 距离中考体考时间越来越近,学校想了解初三年级1512名学生周末在家体育锻炼的情况,在初三年级随机抽取了18名男生和18名女生,对他们周末在家的锻炼时间进行了调查,并收集得到了以下数据(单位:分钟)男生:28,30,32,46,68.39,80,70,66,57,70,95,100,58,69,88,99,105
女生:36,48,78,99,56,62,35,109,29,88,88,69,73,55,90,98,69,72
分析数据:两组数据的平均数、中位数、众数如表所示:
平均数
中位数
众数
方差
男生
66.7
a
70
617.3
女生
69.7
70.5
b
547.2
(1)、若将上面的表格补充完整; ;(2)、已知该年级男女生人数差不多,根据调查的数据,估计初三年级周末在家锻炼的时间在90分钟以上(不包含90分钟)的同学约有多少人?(3)、王老师看了表格数据后认为初三年级的女生周末锻炼做得比男生好,请你结合统计数据,写出两条支持王老师观点的理由.26. 为了调查学生对垃圾分类知识的了解情况,从甲、乙两校各随机抽取20名学生进行了相关知识测试,获得了他们的成绩(百分制,单位:分),并对数据(成绩)进行了整理、描述和分析,下面给出了部分信息.a.甲、乙两校学生样本成绩频数分布表及扇形统计图如图:
甲校学生样本成绩频数分布表(表1)
成绩 (分)
频数
频率
0.10
4
0.20
7
0.35
2
合计
20
1.0
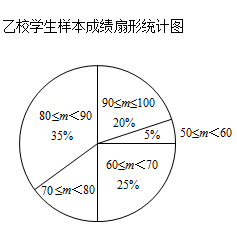
b.甲、乙两校学生样本成绩的平均分、中位数、众数、方差如表所示:(表2)
学校
平均分
中位数
众数
方差
甲
76.7
77
89
150.2
乙
78.1
80
135.3
其中,乙校20名学生样本成绩的数据如下:
54 72 62 91 87 69 88 79 80 62 80 84 93 67 87 87 90 71 68 91
请根据所给信息,解答下列问题:
(1)、表1中 ;表2中的众数 ;(2)、在此次测试中,某学生的成绩是79分,在他所属学校排在前10名,由表中数据可知该学生是校的学生(填“甲”或“乙”),理由是;(3)、乙校学生样本成绩扇形统计图中, 这一组成绩所在扇形的圆心角度数是度;(4)、若甲、乙两校各有1000名学生参加此次测试,成绩80分及以上为优秀,请计算两校成绩优秀的学生大约共为多少人?27. 为了了解某校九年级全体男生 米跑步的成绩,随机抽取了部分男生进行测试.并将测试成绩分为 四个成绩,绘制了如下不完整的统计图表.成绩等级频数分布表


根据图表信息解答下列问题:
(1)、填空: , , 扇形统计图中表示A的扇形的圆心角度数为度;(2)、甲、乙、丙是A等级中的3名学生.学习决定从这3名学生中随机抽取2名来介绍体育锻炼经验,用列表法或画树状图法,求同时抽到甲、乙2学生的概率.