河南省中考数学真题模拟题分类卷5 图形的变换及锐角三角函数(近几年)
试卷更新日期:2021-08-25 类型:二轮复习
一、单选题
-
1. 如下摆放的几何体中,主视图与左视图有可能不同的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图①是由大小相同的小正方体搭成的几何体,将上层的小正方体平移后得到图②.关于平移前后几何体的三视图,下列说法正确的是( )
2. 如图①是由大小相同的小正方体搭成的几何体,将上层的小正方体平移后得到图②.关于平移前后几何体的三视图,下列说法正确的是( )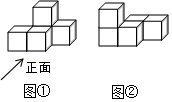 A、主视图相同 B、左视图相同 C、俯视图相同 D、三种视图都不相同3. 如图,胶带的左视图是( )
A、主视图相同 B、左视图相同 C、俯视图相同 D、三种视图都不相同3. 如图,胶带的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 如图是由7个相同的小正方体搭成的几何体,在标号为①的小正方体上方添加一个小正方体后,所得几何体的三视图与原几何体的三视图相比没有发生变化的是( )
4. 如图是由7个相同的小正方体搭成的几何体,在标号为①的小正方体上方添加一个小正方体后,所得几何体的三视图与原几何体的三视图相比没有发生变化的是( ) A、主视图和俯视图 B、主视图和左视图 C、左视图和俯视图 D、主视图、左视图和俯视图5. 下列立体图形的主视图与左视图相同是( )
A、主视图和俯视图 B、主视图和左视图 C、左视图和俯视图 D、主视图、左视图和俯视图5. 下列立体图形的主视图与左视图相同是( ) A、①②③ B、②③ C、①②④ D、①②③④6. 小敏计划在暑假参加海外游学,她打算制作一个正方体礼盒送给外国朋友.如图所示是她设计的礼盒的平面展开图,请你判断,正方体礼盒上与“孝”字相对的面上的字是( )
A、①②③ B、②③ C、①②④ D、①②③④6. 小敏计划在暑假参加海外游学,她打算制作一个正方体礼盒送给外国朋友.如图所示是她设计的礼盒的平面展开图,请你判断,正方体礼盒上与“孝”字相对的面上的字是( )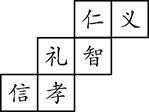 A、义 B、仁 C、智 D、信7. 如图,由5个完全相同的小正方体组合成一个立体图形,它的俯视图是( )
A、义 B、仁 C、智 D、信7. 如图,由5个完全相同的小正方体组合成一个立体图形,它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 如图是由8个相同的小正方体组成的几何体,其主视图是( )
8. 如图是由8个相同的小正方体组成的几何体,其主视图是( )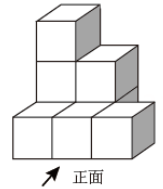 A、
A、 B、
B、 C、
C、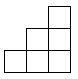 D、
D、 9. 如图, 的顶点 , ,点 在 轴的正半轴上,延长 交 轴于点 .将 绕点 顺时针旋转得到 ,当点 的对应点 落在 上时, 的延长线恰好经过点 ,则点 的坐标为( )
9. 如图, 的顶点 , ,点 在 轴的正半轴上,延长 交 轴于点 .将 绕点 顺时针旋转得到 ,当点 的对应点 落在 上时, 的延长线恰好经过点 ,则点 的坐标为( )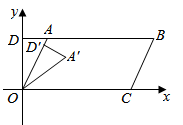 A、 B、 C、 D、10. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“国”字所在面相对的面上的汉字是( )
A、 B、 C、 D、10. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“国”字所在面相对的面上的汉字是( )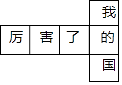 A、厉 B、害 C、了 D、我11. 如图,在 中, ,以点 为圆心, 的长为半径作弧交 于点 ,再分别以点 , 为圆心,大于 的长为半径作弧,两弧交于点 ,作射线 交 于点 .若 , ,则 的值为( )
A、厉 B、害 C、了 D、我11. 如图,在 中, ,以点 为圆心, 的长为半径作弧交 于点 ,再分别以点 , 为圆心,大于 的长为半径作弧,两弧交于点 ,作射线 交 于点 .若 , ,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
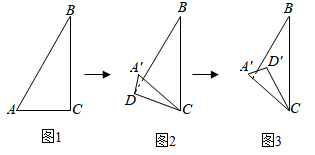
12. 小华用一张直角三角形纸片玩折纸游戏,如图1,在 中, , , .第一步,在 边上找一点 ,将纸片沿 折叠,点 落在 处,如图2,第二步,将纸片沿 折叠,点 落在 处,如图3.当点 恰好在原直角三角形纸片的边上时,线段 的长为.
 13. 如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为 .
13. 如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为 .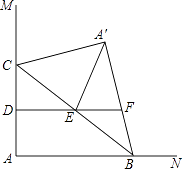 14. 如图,在矩形 中, , ,对角线 , 交于点 ,点 是 边上一动点.将 沿 翻折得到 , 交 于点 ,且点 在 下方,连接 .当 是直角三角形时, 的周长为 .
14. 如图,在矩形 中, , ,对角线 , 交于点 ,点 是 边上一动点.将 沿 翻折得到 , 交 于点 ,且点 在 下方,连接 .当 是直角三角形时, 的周长为 . 15. 如图,在周长为16,面积为6的矩形纸片 中, 是 的中点. 是 上一动点,将 沿直线 折叠,点 落在点 处.在 上任取一点 ,连接 , ,则 的最小值为.
15. 如图,在周长为16,面积为6的矩形纸片 中, 是 的中点. 是 上一动点,将 沿直线 折叠,点 落在点 处.在 上任取一点 ,连接 , ,则 的最小值为. 16. 如图,Rt△ABC中,∠ACB=90°,∠A=30°,BC=6,D,E分别是AB,AC边的中点,将△ABC绕点B顺时针旋转60°到△A′BC′的位置,则整个旋转过程中线段DE所扫过部分的面积(即图中阴影部分面积)为.
16. 如图,Rt△ABC中,∠ACB=90°,∠A=30°,BC=6,D,E分别是AB,AC边的中点,将△ABC绕点B顺时针旋转60°到△A′BC′的位置,则整个旋转过程中线段DE所扫过部分的面积(即图中阴影部分面积)为.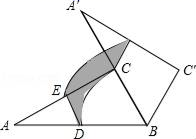 17. 已知:Rt△ABC中,∠B=90°,AB=4,BC=3,点M、N分别在边AB、AC上,将△AMN沿直线MN折叠,点A落在点P处,且点P在射线CB上,当△PNC为直角三角形时,PN的长为.
17. 已知:Rt△ABC中,∠B=90°,AB=4,BC=3,点M、N分别在边AB、AC上,将△AMN沿直线MN折叠,点A落在点P处,且点P在射线CB上,当△PNC为直角三角形时,PN的长为. 18. 如图,在正方形 外作等腰直角三角形 ,连接 ,则 .
18. 如图,在正方形 外作等腰直角三角形 ,连接 ,则 . 19. 如图,在矩形ABCD中, , ,点E在边BC上,且 .连接AE,将 沿AE折叠,若点B的对应点 落在矩形ABCD的边上,则a的值为.
19. 如图,在矩形ABCD中, , ,点E在边BC上,且 .连接AE,将 沿AE折叠,若点B的对应点 落在矩形ABCD的边上,则a的值为. 20. 如图,在矩形ABCD中,AB=6,BC=12,点E在边BC上,且BE=2CE,将矩形沿过点E的直线折叠,点C,D的对应点分别为C′,D′,折痕与边AD交于点F,当点B,C′,D′恰好在同一直线上时,AF的长为.
20. 如图,在矩形ABCD中,AB=6,BC=12,点E在边BC上,且BE=2CE,将矩形沿过点E的直线折叠,点C,D的对应点分别为C′,D′,折痕与边AD交于点F,当点B,C′,D′恰好在同一直线上时,AF的长为.
三、解答题
-
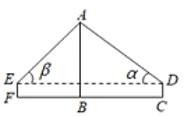
21. 开凿于北魏孝文帝年间的龙门石窟是中国石刻艺术瑰宝,卢舍那佛像是石窟中最大的佛像.某数学活动小组到龙门石窟景区测量这尊佛像的高度.如图,他们选取的测量点 与佛像 的底部 在同一水平线上.已知佛像头部 为 ,在 处测得佛像头顶部 的仰角为 ,头底部 的仰角为 ,求佛像 的高度(结果精确到 .参考数据: , , )
 22. 数学兴趣小组到黄河风景名胜区测量炎帝塑像(塑像中高者)的高度.如图所示,炎帝塑像DE在高55m的小山EC上,在A处测得塑像底部E的仰角为34°,再沿AC方向前进21m到达B处,测得塑像顶部D的仰角为60°,求炎帝塑像DE的高度.(精确到1m.参考数据: , , , )
22. 数学兴趣小组到黄河风景名胜区测量炎帝塑像(塑像中高者)的高度.如图所示,炎帝塑像DE在高55m的小山EC上,在A处测得塑像底部E的仰角为34°,再沿AC方向前进21m到达B处,测得塑像顶部D的仰角为60°,求炎帝塑像DE的高度.(精确到1m.参考数据: , , , )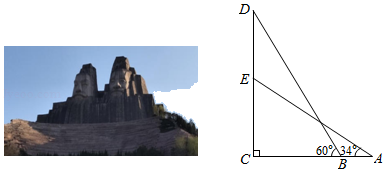 23. “高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.
23. “高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)
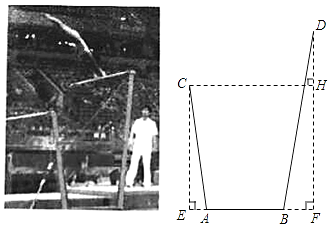 24. 如图,某公园有一小亭 ,它周围350米内是文物保护区.某勘探队员在公园由西向东行走,在 处测得小亭 在北偏东 的方向上,若勘探队员行走的速度是每分钟60米,从点 走到点 需要20分钟,此时测得小亭 在北偏西 的方向上.若该公园打算沿射线 的方向修一条笔直的小路,则此小路是否会通过文物保护区?请说明理由.(结果保留整数.参考数据: , , , )
24. 如图,某公园有一小亭 ,它周围350米内是文物保护区.某勘探队员在公园由西向东行走,在 处测得小亭 在北偏东 的方向上,若勘探队员行走的速度是每分钟60米,从点 走到点 需要20分钟,此时测得小亭 在北偏西 的方向上.若该公园打算沿射线 的方向修一条笔直的小路,则此小路是否会通过文物保护区?请说明理由.(结果保留整数.参考数据: , , , ) 25. 如图,一艘游轮在海面上点O处遇到大雾,向位于A处的救援船发出求救信号,救援船指定B地为相遇地点,其中游轮在救援船的北偏西51°方向上,在相遇点B的南偏西54°方向上,相遇点B在救援船的北偏东9°方向上,救援船以50海里/时的速度行驶2小时到达B地.若游轮的速度是30海里/时,求游轮用多长时间能到达B地.(结果保留一位小数.参考数据: ≈1.41, ≈1.73)
25. 如图,一艘游轮在海面上点O处遇到大雾,向位于A处的救援船发出求救信号,救援船指定B地为相遇地点,其中游轮在救援船的北偏西51°方向上,在相遇点B的南偏西54°方向上,相遇点B在救援船的北偏东9°方向上,救援船以50海里/时的速度行驶2小时到达B地.若游轮的速度是30海里/时,求游轮用多长时间能到达B地.(结果保留一位小数.参考数据: ≈1.41, ≈1.73) 26. 疫情期间,为了保障大家的健康,各地采取了多种方式进行预防,某地利用无人机规劝居民回家.如图,一条笔直的街道 ,在街道 处的正上方 处有一架无人机,该无人机在 处测得俯角为 的街道 处有人聚集,然后沿平行于街道 的方向再向前飞行60米到达 处,在 处测得俯角为 的街道 处也有人聚集,已知两处聚集点 之间的距离为120米,求无人机飞行的高度 .(参考数据: , , , )
26. 疫情期间,为了保障大家的健康,各地采取了多种方式进行预防,某地利用无人机规劝居民回家.如图,一条笔直的街道 ,在街道 处的正上方 处有一架无人机,该无人机在 处测得俯角为 的街道 处有人聚集,然后沿平行于街道 的方向再向前飞行60米到达 处,在 处测得俯角为 的街道 处也有人聚集,已知两处聚集点 之间的距离为120米,求无人机飞行的高度 .(参考数据: , , , )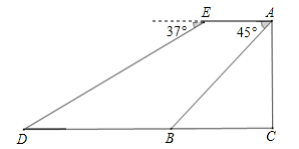
四、综合题
-
27. 位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.

某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水 平步道 上架设测角仪,先在点M处测得观星台最高点A的仰角为 ,然后沿 方向前进 到达点N处,测得点 的仰角为 .测角仪的高度为 ,
(1)、求观星台最高点A距离地面的高度(结果精确到 .参考数据: );(2)、“景点简介”显示,观星台的高度为 ,请计算本次测量结果的误差,并提出一条减小误差的合理化建议.28. 如图 (1)、问题发现
(1)、问题发现如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
① 的值为;
②∠AMB的度数为 .
(2)、类比探究如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断 的值及∠AMB的度数,并说明理由;
(3)、拓展延伸在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB= ,请直接写出当点C与点M重合时AC的长.
29. 中原福塔,又名“河南广播电视塔”,是郑州市著名地标之一.小明和小亮利用卷尺和自制的测角仪测量福塔的高度.如图,小明站在点 处测得福塔顶端 的仰角为 ,小亮站在点 处测得福塔顶端 的仰角为 .已知测角仪高度为 ,两人相距 (点 , , 在一条直线上). (1)、求中原福塔 的高度;(结果精确到 .参考数据: , , , )(2)、“景点简介”显示,中原福塔总高 .请计算本次测量结果的误差,并提出一条减小误差的合理化建议.30. 如图,某人在山坡坡脚 处测得一座建筑物顶点 的仰角为 ,沿山坡向上走到 处再测得该建筑物顶点 的仰角为 .已知 米, , 的延长线交于点 ,山坡坡度为 (即 ).注:取 为 .
(1)、求中原福塔 的高度;(结果精确到 .参考数据: , , , )(2)、“景点简介”显示,中原福塔总高 .请计算本次测量结果的误差,并提出一条减小误差的合理化建议.30. 如图,某人在山坡坡脚 处测得一座建筑物顶点 的仰角为 ,沿山坡向上走到 处再测得该建筑物顶点 的仰角为 .已知 米, , 的延长线交于点 ,山坡坡度为 (即 ).注:取 为 .
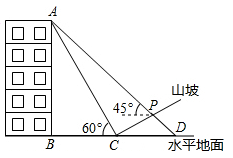 (1)、求该建筑物的高度(即 的长).(2)、求此人所在位置点 的铅直高度(测倾器的高度忽略不计).(3)、若某一时刻, 米长木棒竖放时,在太阳光线下的水平影长是 米,则同一时刻该座建筑物顶点 投影与山坡上点 重合,求点 到该座建筑物的水平距离.31. 蔡明园公园位于河南省驻马店市上蔡县蔡都镇西南部,其公园南山门被誉为“亚洲第一门”,学完了三角函数知识后,某数学“综合与实践”小组的同学把“测量南山门最高点的高度”作为一项课题活动,他们制定了测量方案,并利用课余时间完成了实地测量.为了减小测量误差,小组在测量仰角以及两点间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如表:
(1)、求该建筑物的高度(即 的长).(2)、求此人所在位置点 的铅直高度(测倾器的高度忽略不计).(3)、若某一时刻, 米长木棒竖放时,在太阳光线下的水平影长是 米,则同一时刻该座建筑物顶点 投影与山坡上点 重合,求点 到该座建筑物的水平距离.31. 蔡明园公园位于河南省驻马店市上蔡县蔡都镇西南部,其公园南山门被誉为“亚洲第一门”,学完了三角函数知识后,某数学“综合与实践”小组的同学把“测量南山门最高点的高度”作为一项课题活动,他们制定了测量方案,并利用课余时间完成了实地测量.为了减小测量误差,小组在测量仰角以及两点间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如表:课题
测量南山门最高点的高度
实物图

成员
组长:xxx
组员:xxx,xxx,xxx
测量工具
卷尺、测角仪……
测量示意图
说明:AB表示南山门最高点到地面的竖直距离.测角仪的高度CD-EF-1.5m点C.F与点B在同一直线上,点C.F之间的距离可直接测将,且点A、B.C.D.E、F在同一平面内.
测量数据
第一次
第二次
平均值
35.95°
36.05°
36°
45.09°
44.91°
45°
79.58m
79.62m
79.6m
……
……
(1)、请帮助该小组的同学根据上表中的测量数据,求南山门最高点的高度AB.(结果精确到0.1m,参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73, ≈1.41)(2)、该小组要写出一份完整的课题活动报告,除上表中的项目外,你认为还需要补充哪些项目?(写出一个即可)(如需作图或作辅助线,请先将原题草图画在对应题目的答题区域后再作答.)32. 在古代,智慧的劳动人民已经会使用“石磨”,其原理为在磨盘的边缘连接一个固定长度的“连杆”,推动“连杆”带动磨盘转动,将粮食磨碎,物理学上称这种动力传输工具为“曲柄连杆机构”.小明受此启发设计了一个“双连杆机构”,设计图如图1,两个固定长度的“连杆” , 的连接点 在 上,当点 在 上转动时,带动点 , 分别在射线 , 上滑动, .当 与 相切时,点 恰好落在 上,如图2.
请仅就图2的情形解答下列问题.
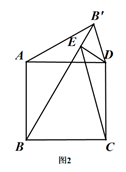
(1)、求证: ;(2)、若 的半径为 , ,求 的长.33. 将正方形 的边 绕点A逆时针旋转至 ,记旋转角为 .连接 ,过点D作 垂直于直线 ,垂足为点E,连接 ,(1)、如图1,当 时, 的形状为 ,连接 ,可求出 的值为; (2)、当 且 时,
(2)、当 且 时,①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;
②当以点 为顶点的四边形是平行四边形时,请直接写出 的值.
 34. 在 , , .点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.
34. 在 , , .点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.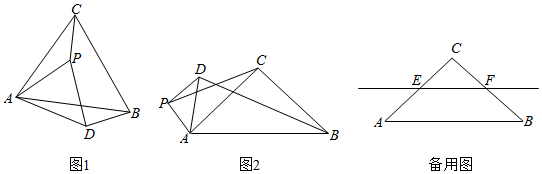 (1)、观察猜想
(1)、观察猜想如图1,当 时, 的值是 , 直线BD与直线CP相交所成的较小角的度数是.
(2)、类比探究如图2,当 时,请写出 的值及直线BD与直线CP相交所成的小角的度数,并就图2的情形说明理由.
(3)、解决问题当 时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时 的值.
35. 如图,在菱形 中, ,将边 绕点 逆时针旋转至 ,记旋转角为 .过点 作 于点 ,过点 作 直线 于点 ,连接 . (1)、(探索发现)
(1)、(探索发现)
填空:当 时, = . 的值是(2)、(验证猜想)
当 时,(1)中的结论是否仍然成立?若成立,请仅就图2的情形进行证明;若不成立,请说明理由;(3)、(拓展应用)
在(2)的条件下,若 ,当 是等腰直角三角形时,请直接写出线段 的长.36. 在 中, , ,点P是平面内不与点A,C重合的任意一点,连接CP,将线段CP绕点P旋转 得到线段DP,连结AP,CD,BD.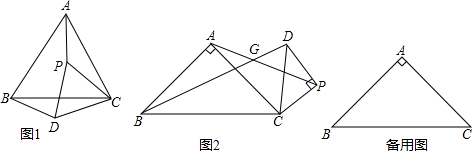 (1)、观察猜想:如图1,当 时,线段CP绕点P顺时针旋转 得到线段DP,则 的值是 , 直线AP与BD相交所成的较小角的度数是;(2)、类比探究:如图2,当 时,线段CP绕点P顺时针旋转 得到线段 请直接写出AP与BD相交所成的较小角的度数,并说明 与 相似,求出 的值;(3)、拓展延伸:当 时,且点P到点C的距离为 ,线段CP绕点P逆时针旋转 得到线段DP,若点A,C,P在一条直线上时,求 的值.37. 如图①,△ABC为直角三角形,∠ACB=90°,∠BAC=30°,点D在AB边上,过点D作DE⊥AC于点E,取BC边的中点F,连接DF并延长到点G,使FG=DF,连接CG.(如需作图或作辅助线,请先将原题草图画在对应题目的答题区域后再作答.)
(1)、观察猜想:如图1,当 时,线段CP绕点P顺时针旋转 得到线段DP,则 的值是 , 直线AP与BD相交所成的较小角的度数是;(2)、类比探究:如图2,当 时,线段CP绕点P顺时针旋转 得到线段 请直接写出AP与BD相交所成的较小角的度数,并说明 与 相似,求出 的值;(3)、拓展延伸:当 时,且点P到点C的距离为 ,线段CP绕点P逆时针旋转 得到线段DP,若点A,C,P在一条直线上时,求 的值.37. 如图①,△ABC为直角三角形,∠ACB=90°,∠BAC=30°,点D在AB边上,过点D作DE⊥AC于点E,取BC边的中点F,连接DF并延长到点G,使FG=DF,连接CG.(如需作图或作辅助线,请先将原题草图画在对应题目的答题区域后再作答.) (1)、问题发现:
(1)、问题发现:填空:CE与CG的数量关系是 , 直线CE与CG所夹的锐角的度数为.
(2)、探究证明:将△ADE绕点A逆时针旋转,(1)中的结论是否仍然成立,若成立,请仅就图②所示情况给出证明,若不成立,请说明理由;
(3)、问题解决:若AB=4,AD=3,将△ADE由图①位置绕点A逆时针旋转α(0°<α<180°),当△ACE是直角三角形时,请直接写出CG的值.
38. 如图 (1)、观察猜想:如图1,在 中, , , 是 的平分线,以 为一边作正方形 ,点 与点 重合,则 .(2)、类比探究:在(1)的条件下,如果正方形 绕点 旋转,连接 、 、 ,(1)中的结论是否成立?请按图2加以证明.(3)、问题解决:当正方形 旋转到 、 、 三点共线时,请直接写出线段 的长.39. 在△ABC中,∠ACB=90°,AC=BC=2,D是射线BC上一动点,过点B作BE⊥AD,垂足为点E,交直线AC于点P.
(1)、观察猜想:如图1,在 中, , , 是 的平分线,以 为一边作正方形 ,点 与点 重合,则 .(2)、类比探究:在(1)的条件下,如果正方形 绕点 旋转,连接 、 、 ,(1)中的结论是否成立?请按图2加以证明.(3)、问题解决:当正方形 旋转到 、 、 三点共线时,请直接写出线段 的长.39. 在△ABC中,∠ACB=90°,AC=BC=2,D是射线BC上一动点,过点B作BE⊥AD,垂足为点E,交直线AC于点P. (1)、(问题发现)
(1)、(问题发现)如图①,若点D在BC的延长线上,试猜想AP,CD,BC之间的数量关系为;
(2)、(类比探究)如图②,若点D在线段BC上,试猜想AP,CD,BC之间的数量关系,并说明理由;
(3)、(拓展应用)当E为BP的中点时,直接写出线段CD的长度.
40. 如图 (1)、问题发现
(1)、问题发现如图①,△ABC和△CDE均为等边三角形,直线AD和直线BE交于点F.
填空:①∠AFB的度数是;
②线段AD,BE之间的数量关系为.
(2)、类比探究如图②,△ABC和△CDE均为等腰直角三角形,∠ABC=∠DEC=90°,AB=BC,DE=EC,直线AD和直线BE交于点F.请判断∠AFB的度数及线段AD,BE之间的数量关系,并说明理由.
(3)、解决问题如图③,在平面直角坐标系中,点A的坐标为(4,0),点B为y轴上任意一点,连接AB,将BA绕点B逆时针旋转90°至BC,连接OC,请直接写出OC的最小值.
41. 定义:长宽比为 :1(n为正整数)的矩形称为 矩形.下面,我们通过折叠的方式折出一个 矩形,如图a所示.

操作1:将正方形ABEF沿过点A的直线折叠,使折叠后的点B落在对角线AE上的点G处,折痕为AH.
操作2:将FE沿过点G的直线折叠,使点F、点E分别落在边AF,BE上,折痕为CD.则四边形ABCD为 矩形.
(1)、证明:四边形ABCD为 矩形;(2)、点M是边AB上一动点.①如图b,O是对角线AC的中点,若点N在边BC上,OM⊥ON,连接MN.求tan∠OMN的值;
②若AM=AD,点N在边BC上,当△DMN的周长最小时,求 的值;
③连接CM,作BR⊥CM,垂足为R.若AB=2 ,则DR的最小值= .